При выводе уравнения (1.1) постулировалось, что зародыши представляют собой сферические капли с поверхностным натяжением, характерным для массивной фазы. Такая модель описывает изотропное формирование зародышей, для которых равновесной формой является шар. Если результатом зародышеобразования являются твердые кристаллические продукты, в частности металлсодержащие ансамбли, то формирование термодинамически равновесного кристаллического зародыша происходит анизотропно в силу кристаллографической неравноценности поверхностной энергии его границы: меняются площадь поверхности, плотность и взаимное расположение атомов в поверхностном слое.
В ходе образования зародышей различные элементы поверхностей раздела и сами поверхности создаются и исчезают. С учетом этого второе слагаемое  в уравнении энергии Гиббса образования кристаллического зародыша следует записывать в виде суммы нескольких членов:
в уравнении энергии Гиббса образования кристаллического зародыша следует записывать в виде суммы нескольких членов:
 (10.)
(10.)
где  и
и  - соответственно удельная свободная поверхностная энергия и площадь поверхности грани h кристалла;
- соответственно удельная свободная поверхностная энергия и площадь поверхности грани h кристалла;  - длина нормали из центра кристаллического зародыша до грани
- длина нормали из центра кристаллического зародыша до грани 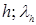 - коэффициент формы (параметр, зависящий от формы кристалла).
- коэффициент формы (параметр, зависящий от формы кристалла).

Так, в простейшем случае образования кубического зародыша со стороной а выражение (1) для полного изменения энергии Гиббса преобразуется к виду
 . (9.а)
. (9.а)
Для куба критического размера 
 (11.)
(11.)
и, соответственно, потенциальный барьер появления критического зародыша будет равен
 (12)
(12)
Полагая, что поверхностные энергии шара и грани куба близки, получаем  (куб)
(куб)  (шар), т.е. потенциальный барьер зародышеобразования в случае зародыша кубической формы почти вдвое выше, чем для сферического. Это подтверждает известное положение, важное и для металлополимерных систем, что наиболее вероятной равновесной формой изотропно образованного кристаллического зародыша является шарообразная, отвечающая минимуму энергии и используемая при вычислении энергетического барьера образования зародыша. Основные концепции рассмотренной выше изотропной мо дели зародышеобразования при конденсации из паровой фазы не претерпевают принципиального изменения при рассмотрении изотропного образования новой фазы в растворе или расплаве. При этом в уравнении (1) изменяется лишь содержание выражения для
(шар), т.е. потенциальный барьер зародышеобразования в случае зародыша кубической формы почти вдвое выше, чем для сферического. Это подтверждает известное положение, важное и для металлополимерных систем, что наиболее вероятной равновесной формой изотропно образованного кристаллического зародыша является шарообразная, отвечающая минимуму энергии и используемая при вычислении энергетического барьера образования зародыша. Основные концепции рассмотренной выше изотропной мо дели зародышеобразования при конденсации из паровой фазы не претерпевают принципиального изменения при рассмотрении изотропного образования новой фазы в растворе или расплаве. При этом в уравнении (1) изменяется лишь содержание выражения для  = j
= j  (табл. 1.1).
(табл. 1.1).
Иная картина наблюдается при формировании новой фазы в твердой матрице, для которой, как правило, характерна пространственная анизотропия свойств, например, при переходе из одной фазы (кристаллической или аморфной) в другую - кристаллическую, в частности при полимеризационных превращениях. Возникновение зародыша новой фазы со своим удельным объемом и структурой, отличными от материнской, приводят к появлению напряжений, возникающих при деформации решетки в результате фазового превращения (образования зародыша). В таком случае, если  - деформация решетки, вызванная образованием зародыша материнской фазы и характеризующая при
- деформация решетки, вызванная образованием зародыша материнской фазы и характеризующая при 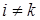 сдвиг;
сдвиг;  соответствующее относительное изменение объема;
соответствующее относительное изменение объема;  - модуль сдвига (отношение угла сдвига к касательному напряжению), то при условии, что модули сдвига материнской и новой фазы одинаковы, а множители, содержащие коэффициент формы зародыша и коэффициенты Пуассона (отношение относительного поперечного сжатия к относительному продольному изменению), принять равными единице, то возникающую упругую энергию матрицы и зародыша в общем виде можно представить как
- модуль сдвига (отношение угла сдвига к касательному напряжению), то при условии, что модули сдвига материнской и новой фазы одинаковы, а множители, содержащие коэффициент формы зародыша и коэффициенты Пуассона (отношение относительного поперечного сжатия к относительному продольному изменению), принять равными единице, то возникающую упругую энергию матрицы и зародыша в общем виде можно представить как  . Как и поверхностная энергия
. Как и поверхностная энергия  , упругая энергия
, упругая энергия 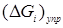 , пропорциональна объему зародыша, ее увеличение приводит к возрастанию энергии Гиббса системы.
, пропорциональна объему зародыша, ее увеличение приводит к возрастанию энергии Гиббса системы.
Оценим, насколько сопоставимы  и
и 
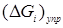

 ].
].
Используя типичные значения  Дж/см
Дж/см 
 Дж/см
Дж/см  ,
, 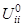
 получаем, что когда линейный размер зародыша
получаем, что когда линейный размер зародыша 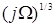
 1,0 нм (несколько межатомных расстояний), упругая и поверхностная энергии сопоставимы.
1,0 нм (несколько межатомных расстояний), упругая и поверхностная энергии сопоставимы.
При этом для 
 см
см  получаем j
получаем j  50.
50.
Полное изменение энергии Гиббса системы при твердофазном образовании зародыша
гомогенный изотропный зародыш твердофазный
 G
G  =(
=( G
G  )
) 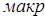 +(
+( G
G  )
)  +(
+( G
G  )
)  =
=  (13)
(13)
Очевидно, зарождение новой фазы происходит лишь при условии, что  >
>  . Это возможно (используем приведенные выше значения
. Это возможно (используем приведенные выше значения 
 ), когда
), когда  Дж.
Дж.
Если
 ,
,
где  - теплота перехода (как правило,
- теплота перехода (как правило,  Дж);
Дж);  - температура перехода,
- температура перехода,  =
=  -переохлаждение, то новая фаза может формироваться в объеме твердой материнской, если относительное переохлаждение
-переохлаждение, то новая фаза может формироваться в объеме твердой материнской, если относительное переохлаждение 
 0,3. Когда в материнской фазе релаксация напряжений протекает за времена, значительно превышающие времена зарождения, т.е. по отношению к зародышу материнскую фазу можно считать жесткой, то образование зародыша при
0,3. Когда в материнской фазе релаксация напряжений протекает за времена, значительно превышающие времена зарождения, т.е. по отношению к зародышу материнскую фазу можно считать жесткой, то образование зародыша при 
 0,3 термодинамически не выгодно.
0,3 термодинамически не выгодно.
Критический зародыш возникает, когда  0, и, следовательно,
0, и, следовательно,
 (14)
(14)
При  Дж/см
Дж/см  ,
,  Дж/см
Дж/см  ,
, 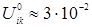 ,
,  см
см  и
и  Дж получаем
Дж получаем  . Соответственно
. Соответственно 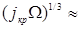 1,4 нм.
1,4 нм.
Все сказанное выше об особенностях зарождения новой фазы относится к твердым телам с идеальной кристаллической решеткой. В реальных кристаллических телах всегда присутствуют дефекты решетки, такие как дефекты упаковки, дислокации и дислокационные системы, структурные комплексы, создаваемые примесями и междоузельными атомами, границы зерен и доменов и т.п., которые повышают
термодинамический потенциал кристалла. Поэтому образование определенным образом расположенных относительно них областей новой фазы может быть сопряжено с выигрышем энергии по сравнению с образованием подобных областей в идеальной решетке. Энергия, необходимая для создания критического зародыша в идеальной решетке, достаточно велика, и поэтому для зародышеобразования требуются в этих условиях значительные отклонения от условий равновесия фаз. Наличие дефектов приводит к уменьшению этой энергии, катализирует процесс зародышеобразования в некоторых случаях настолько, что зарождение новой фазы может протекать без преодоления значительных энергетических барьеров, с энергией активации порядка энергии активации диффузии.
Качественно общую картину зарождения когерентной фазы можно представить следующим образом. Образование зародыша - участка когерентной фазы в некоторой ограниченной области кристалла и приводит к изменению энергии Гиббса кристалла, которое при существовании достаточно резкой границы раздела фаз можно представить в виде суммы трех слагаемых:
 (13.а)
(13.а)
Первое слагаемое в этом соотношении отражает изменения, связанные с возникновением поверхности раздела фаз, и пропорционально площади поверхности раздела S,  =
=  S > 0, где
S > 0, где  - удельная поверхностная энергия. С увеличением характерного размера зародыша R эта энергия возрастает как ~ R
- удельная поверхностная энергия. С увеличением характерного размера зародыша R эта энергия возрастает как ~ R  .
.
Второй член, пропорциональный объему V, учитывает вклад как изменения химического потенциала фаз  при превращении, так и работы на создание напряжений в ходе превращения:
при превращении, так и работы на создание напряжений в ходе превращения:

 (15)
(15)
где  - модуль сдвига;
- модуль сдвига;  - наибольший компонент тензора деформации превращения
- наибольший компонент тензора деформации превращения  ;
;  - числовой множитель, зависящий от формы области и деформации.
- числовой множитель, зависящий от формы области и деформации.
С увеличением R энергия  повышается как R
повышается как R  . Третье слагаемое в (13.а) отражает вклад взаимодействия зародыша с полем упругих напряжений
. Третье слагаемое в (13.а) отражает вклад взаимодействия зародыша с полем упругих напряжений  дефекта кристаллической решетки:
дефекта кристаллической решетки:
 (16)
(16)
и с ростом R убывает ~ R  - закон убывания напряжения дефекта. Вследствие разного хода зависимости членов в выражении (13.а) от характерного размера зародыша и различным их вкладом в изменение энергии, с ростом R потенциал
- закон убывания напряжения дефекта. Вследствие разного хода зависимости членов в выражении (13.а) от характерного размера зародыша и различным их вкладом в изменение энергии, с ростом R потенциал  сначала увеличивается, но после достижения некоторого критического значения R
сначала увеличивается, но после достижения некоторого критического значения R  , соответствующего критическому зародышу, убывает. Форму критического зародыша находят из условия обращения в нуль первой производной
, соответствующего критическому зародышу, убывает. Форму критического зародыша находят из условия обращения в нуль первой производной  . При этом средняя кривизна в некоторой точке поверхности критического зародыша определяется разностью химических потенциалов фаз
. При этом средняя кривизна в некоторой точке поверхности критического зародыша определяется разностью химических потенциалов фаз  , поверхностной энергией зародыша
, поверхностной энергией зародыша  , полной деформацией зародыша
, полной деформацией зародыша  и полным напряжением в этой точке
и полным напряжением в этой точке
 (17)
(17)
где  напряжение, создаваемое зародышем
напряжение, создаваемое зародышем
Зарождение новой фазы на линейных дефектах (дислокациях) - явление чрезвычайно распространенное при превращениях в твердом теле. Напряжения дислокации убывают с расстоянием r от ее оси как  , где параметр
, где параметр  зависит от ориентации дислокации и вида зародыша и в целом характеризует убыль поверхностного натяжения зародыша в поле дислокации. Вследствие того, что в этом случае показатель убывания напряжения
зависит от ориентации дислокации и вида зародыша и в целом характеризует убыль поверхностного натяжения зародыша в поле дислокации. Вследствие того, что в этом случае показатель убывания напряжения  , подобно
, подобно  возрастает с увеличением характерного размера зародыша R пропорционально R
возрастает с увеличением характерного размера зародыша R пропорционально R  , оставаясь отрицательным, но по размерности совпадая с
, оставаясь отрицательным, но по размерности совпадая с  .
.
Вблизи от дислокации, в зависимости от ее ориентации, существуют области как наиболее выгодные, так и наиболее невыгодные для образования новой фазы. По мере приближения к дислокации кривизна поверхности критического зародыша стремится к бесконечности. Совокупность этих обстоятельств приводит к тому, что критический зародыш представляет собой наблюдаемую экспериментально веретенообразную фигуру, вытянутую вдоль дислокации. Изменение параметра  приводит к тому, что при его приближении к
приводит к тому, что при его приближении к  энергия образования критического зародыша
энергия образования критического зародыша  ~
~  стремится к нулю, причем зародыш все более прижимается к дислокации. При А
стремится к нулю, причем зародыш все более прижимается к дислокации. При А  на дислокации возможно безбарьерное зарождение новой фазы.
на дислокации возможно безбарьерное зарождение новой фазы.
При структурных превращениях, как и при когерентных, происходит однородная перестройка решетки. Однако в случае когерентных превращений степень искривления кристаллической решетки мала, и возможно когерентное сопряжение старой и новой фаз. Структурные же превращения, протекающие с изменением симметрии решетки, могут сопровождаться значительными ее искривлениями, требующими больших энергетических затрат. Дефекты кристалла, создающие большие локальные искажения решетки, способны, однако, перестроить часть материала около себя до состояния, близкого к решетке новой фазы.
Подчеркнем, что для образования в однокомпонентной гомогенной системе зародышей новой фазы, способных к дальнейшему росту необходимо значительное смещение фазы в метастабильную область, приводящее к достаточному для достижения критического состояния пересыщению (переохлаждению). Рассмотренные модели гомогенного зародышеобразования позволяют оценить уровень критического пересыщения, размер и количественный состав критического зародыша.