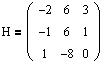Собственные векторы и собственные значения
Пусть A – матрица некоторого линейного преобразования порядка n.
Определение. Многочлен n-ой степени
P(l)=det(A-lЕ) (1.1)
называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.
Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию
А(х)=lх, (1.2)
называется собственным вектором преобразования A. Число l называется собственным значением.
Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:
Ах=lх, (1.3)
где A – матрица преобразования, x – координатный столбец.
Определение. Алгебраической кратностью собственного значения lj называется кратность корня lj характеристического многочлена.
Определение. Совокупность всех собственных значений называется спектром матрицы.
Алгоритм нахождения собственных значений и собственных векторов
1. Найти собственные значения матрицы:
· записать характеристическое уравнение:
det(A-lЕ)=0; (1.4)
· найти его корни l j, j=1,...,n и их кратности.
2. Найти собственные векторы матрицы:
· для каждого l j решить уравнение
(A-l jE)x=0; (1.5)
· найденный вектор х и будет собственным вектором, отвечающим собственному значению l j.
Пример1
Найдем собственные значения и собственные векторы, если известна матрица преобразования:
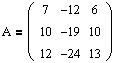
Записываем характеристический многочлен (1.1) и решаем характеристическое уравнение (1.4):
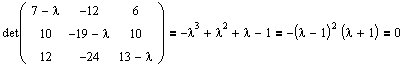
Получаем два собственных значения: l1=1 кратности m1=2 и l2=-1 кратности m2=1.
Далее с помощью соотношения (1.5) находим собственные векторы. Сначала ищем ФСР для l1=1:
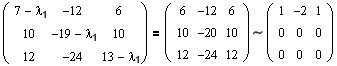
Очевидно, что rang=1, следовательно, число собственных векторов для l1=1 равно n-rang=2. Найдем их:
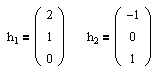
Аналогичным образом находим собственные векторы для l2=-1. В данном случае будет один вектор:
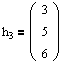
Понятие жордановой клетки и жордановой матрицы
Определение. Жордановой клеткой порядка m, отвечающей собственному значению l, называется матрица вида:
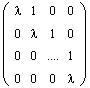(2.1)
Иными словами, на главной диагонали такой матрицы располагается собственное значение l, диагональ, ближайшая к главной, сплошь занята единицами, а все остальные элементы матрицы равны нулю. Ниже даны примеры жордановых клеток соответственно первого, второго и третьего порядков:
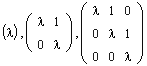
Определение. Блочно-диагональная матрица, на диагонали которой стоят жордановы клетки, называется жордановой матрицей:
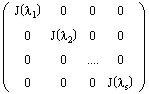(2.2)
ex2
Пример
Ниже представлена жорданова матрица, состоящая из трех жордановых клеток:
- размера 1, отвечающая собственному значению l1=3;
- размера 2, отвечающая собственному значению l2=4;
- размера 3, отвечающая собственному значению l3=5.
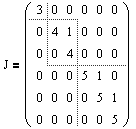
Количество и размер жордановых клеток
Пусть А - матрица, которую нужно привести к жордановой форме, lj (k=1,...,mj) - собственные значения этой матрицы.
Количество жордановых клеток размера k, отвечающих собственному значению lj, определяется следующим образом:
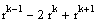(3.1)
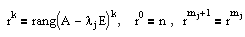(3.2)
где k=1,...,mj, mj - кратность корня lj,
ex3
Пример
Пусть дана матрица преобразования:
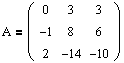
Найдем количество и размер жордановых клеток, соответствующих каждому собственному значению этого преобразования.
Как искать собственные значения, было подробно рассказано в первом параграфе учебника. Поэтому опустим все расчеты, а сразу укажем собственные числа матрицы А: l1=0 кратности m1=1 и l2=-1 кратности m2=2.
Используя соотношения (3.1) и (3.2), найдем количество и размер жордановых клеток, соответствующих l1=0, m1=1.
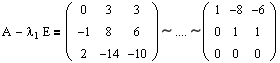
Очевидно, что rang(A-l1E)=2 и, соответственно, r1=r2=rang(A-l1E)1=2, r0=n=3.
Количество жордановых клеток размера 1 будет равно: r0-2r1+r2=3-2*2+2=1.
Ясно, что других клеток для этого собственного значения нет. Т.о., для l1=0, m1=1 мы имеем единственную жорданову клетку вида J1(0)=(0).
Далее аналогичным образом определяем клетки для второго собственного значения l2=-1 кратности m2=2.
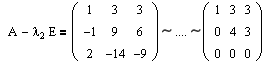
Очевидно, что rang(A-l2E)=2 и, соответственно, r1=r2=rang(A-l2E)1=2.
Далее:
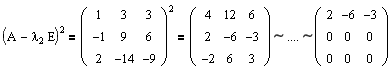
Т.е. rang(A-l1E)2=1 и, соответственно, r1=r2=rang(A-l1E)2=1.
Теперь можно определить количество и размер жордановых клеток для второго собственного значения:
- размера 1: r0-2r1+r2=3-2*2+1=0;
- размера 2: r1-2r2+r3=2-2*1+1=1.
Таким образом, для l2=-1 мы получили одну клетку размера 2:
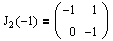
Соответственно, жорданова форма для исходной матрицы А будет иметь вид:
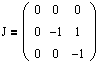
Жорданов базис
Пусть матрица А приведена к жордановой форме J. Рассмотрим систему HJ=AH, где
H=(hij) (4.1)
- матрица перехода от исходного базиса (e) к жорданову базису (h). Это система матричных n2 уравнений с n2 неизвестными.
Определение. Пусть e – собственный вектор преобразования А, т.е. имеет место равенство А(e) = le. Вектор e1, удовлетворяющий равенству
А(e1) = le1+e, (4.2)
называется присоединенным вектором первого порядка;
вектор e2, удовлетворяющий равенству
А(e2) = le2+e1, (4.3)
- присоединенным вектором второго порядка;
...
вектор en, удовлетворяющий равенству
А(en) = len+en-1, (4.4)
- присоединенным вектором n-ого порядка.
Заметим также, что
(А-lе)kek=e. (4.5)
Алгоритм нахождения векторов жорданова базиса
Чтобы найти жорданов базис, необходимо проделать следующие действия для каждой жордановой клетки.
Рассмотрим жорданову клетку порядка k, отвечающую собственному значению l. Для нее ищутся вектора жорданова базиса:
h, h1, h2,...,hk-1, где:
h - собственный вектор, отвечающий собственному значению l;
h1 - присоединенный вектор 1-ого порядка;
h2 - присоединенный вектор 2-ого порядка;
...
hk-1 - присоединенный вектор (k-1)-ого порядка;
Эта совокупность векторов ищется, используя следующую систему:
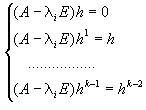(4.6)
В результате применения этих операций ко всем жордановым клеткам, получим векторы, составляющие жорданов базис:
h, h1, h2,...,hk-1, f, f1, f2,...,fp-1,...
Векторам h соответствует жорданова клетка размера k, векторам f – размера p и т.д.
ex3
Пример
Вернемся к примеру, рассмотренному в прошлом разделе. Там нами были получены две жордановы клетки:
J1(0)=(0) и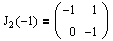
Рассмотрим первую, J1(0).
С помощью соотношения (1.5) из первого параграфа найдем собственный вектор, отвечающий собственному значению l1=0:
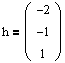
Присоединенных векторов для данной жордановой клетки, очевидно, нет.
Теперь рассмотрим вторую жорданову клетку, J2(-1). Очевидно, что для нее надо найти один собственный вектор и один присоединенный.
Используя систему (4.6), получим эти векторы:
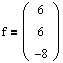- собственный вектор, отвечающий l2=-1;
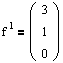- присоединенный вектор.
Мы получили все векторы, составляющие матрицу Н. Таким образом, матрица перехода к жорданову базису будет иметь следующий вид:
