Комплексное число  можно записать в тригонометрической форме:
можно записать в тригонометрической форме:

Тригонометрическая форма КЧ употребляется при возведении КЧ в n-ую степень и при извлечении корня n-ой степени из КЧ:
Формула Муавра: 
Формула вычислений квадратного корня:
 , k=1,2,3,…
, k=1,2,3,…
Тригонометрическая форма комплексного числа(КЧ), изображение на плоскости
Комплексное число
Тригонометрическая форма КЧ употребляется при возведении КЧ в n-ую степень и при извлечении корня n-ой степени из КЧ: Формула Муавра: Формула вычислений квадратного корня:
| 55.Тригонометрическая форма комплексного числа(КЧ), изображение на плоскости
Комплексное число  можно записать в тригонометрической форме: можно записать в тригонометрической форме:
 Тригонометрическая форма КЧ употребляется при возведении КЧ в n-ую степень и при извлечении корня n-ой степени из КЧ:
Формула Муавра:
Тригонометрическая форма КЧ употребляется при возведении КЧ в n-ую степень и при извлечении корня n-ой степени из КЧ:
Формула Муавра:  Формула вычислений квадратного корня:
Формула вычислений квадратного корня:
 , k=1,2,3,… , k=1,2,3,…
 Пусть а = α + iβ - произвольное комплексное число. Соединим начало координат с точкой А(α,β) и длину полученного отрезка обозначим r. Угол между положительным направлением оси абсцисс и направлением из начала координат на эту точку обозначим Пусть а = α + iβ - произвольное комплексное число. Соединим начало координат с точкой А(α,β) и длину полученного отрезка обозначим r. Угол между положительным направлением оси абсцисс и направлением из начала координат на эту точку обозначим  .
Из прямоугольного треугольника ОАВ имеем: .
Из прямоугольного треугольника ОАВ имеем:
 α = r cos α = r cos  , β = r sin , β = r sin  (1.1)
При этом, очевидно (1.1)
При этом, очевидно  Подставляя α и β из (1.1) в формулу а = α + iβ получаем тригонометрическую форму записи комплексного числа а: а = r (cos
Подставляя α и β из (1.1) в формулу а = α + iβ получаем тригонометрическую форму записи комплексного числа а: а = r (cos  + isin + isin  ). ).
| |||
57.Комплексное число в показательной форме. Формула Эйлера. Действия над комплексными числами в показательной форме.
Используя формулу Эйлера
 ,
Комплексное число z=r( ,
Комплексное число z=r(  ) можно записать в показательной (или экспоненциальной) форме z=r ) можно записать в показательной (или экспоненциальной) форме z=r  , где r= , где r=  – модуль комплексного числа, а угол – модуль комплексного числа, а угол  = =  . Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т.е. считать . Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т.е. считать  .
Сложение: сумма двух комплексных чисел .
Сложение: сумма двух комплексных чисел  и и 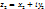 – это компл.число, определяемое равенством – это компл.число, определяемое равенством 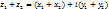 .
Вычитание – действие, обратное сложению. .
Вычитание – действие, обратное сложению.  . Отсюда получаем, что . Отсюда получаем, что  Умножение: произведение компл.чисел
Умножение: произведение компл.чисел  и и 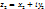 - это компл.число, определяемое формулой - это компл.число, определяемое формулой  .
Отсюда следует важн.соотношение: .
Отсюда следует важн.соотношение:  Благодаря этому соотношен. Формула произведения получается путем перемножения двучленов Благодаря этому соотношен. Формула произведения получается путем перемножения двучленов  и и  .
Умножение компл.чисел обладает переместительными свойствами: .
Умножение компл.чисел обладает переместительными свойствами:  ; ( ; ( ) )  = =  ); );  )= )=  + +  .
При умножении компл.чисел из модули перемножаются, а аргументы складываются. Это правило рапространяется на любое конечное число множителей. Если есть n множителей и все они одинаковые, то: .
При умножении компл.чисел из модули перемножаются, а аргументы складываются. Это правило рапространяется на любое конечное число множителей. Если есть n множителей и все они одинаковые, то:  . – Формула Муавра.
Деление – действие, обратное умножению. . – Формула Муавра.
Деление – действие, обратное умножению. 
| 58.Определение производной функции в точке. Геометрический и механический смысл производной.
Производной функции в точке  в точке в точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.По определению называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.По определению
 или или
 Функция
Функция  , имеющая производную в каждой точке интервала называется дифференцируемой в этом интервале, операция нахождения производной функции называется дифференцированием.
Значение производной функции в точке , имеющая производную в каждой точке интервала называется дифференцируемой в этом интервале, операция нахождения производной функции называется дифференцированием.
Значение производной функции в точке  в точке в точке  обозначается обозначается  .
Скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t – мех. Смысл производной.
Геом. Смысл: производная .
Скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t – мех. Смысл производной.
Геом. Смысл: производная  в точке х равно угловому коэффициенту касательной к графику функции в точке х равно угловому коэффициенту касательной к графику функции  в точке, абсцисса которой равна х. в точке, абсцисса которой равна х.
| 59. Экономический смысл производной.
Пусть U=U(t) – функция, выражающая объем произведенной продукции за время t.
Тогда за  объем произведенной продукции объем произведенной продукции   Если использовать понятие
Если использовать понятие  , то производная труда в момент времени , то производная труда в момент времени  называется пределом называется пределом
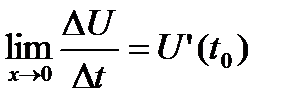 О. эластичностью ф-ии
О. эластичностью ф-ии  наз. величину наз. величину
 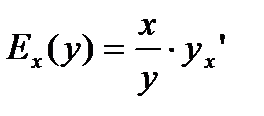 , которая выражает приближенный %- ный прирост значения ф-ии при приросте аргумента на 1%. , которая выражает приближенный %- ный прирост значения ф-ии при приросте аргумента на 1%.
| 60. Основные правила дифференцирования.
Дифф - процесс вычисления производной.
Ф-ия называется дифференцируемой в точке если она имеет в этой точке конечную производную.
Теорема 1. Если U=U(x) и V=V(x) дифф. в точке x, то ф-ия 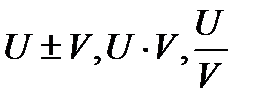  также дифф. в этой точке. также дифф. в этой точке.

| 62Логарифмическая произв-я.диффер-е ф-ии,заданных неявно
В некоторых случаях для нахождения производной сложную функцию сначала логарифмируют:
lnx+lny = lnx  y;
lnx-lny = ln y;
lnx-lny = ln  ;
lnxy = ylnx.
Рассмотрим функцию заданную неявно F(x,y)=0:
Для нахождения производной функции, заданной неявно, достаточно продифференцировать исходное уравнение по переменнойх,считая у – функцией от х.
Рассмотрим функцию заданную параметрически: ;
lnxy = ylnx.
Рассмотрим функцию заданную неявно F(x,y)=0:
Для нахождения производной функции, заданной неявно, достаточно продифференцировать исходное уравнение по переменнойх,считая у – функцией от х.
Рассмотрим функцию заданную параметрически:
 ;
Вычисление производной производится по формуле ;
Вычисление производной производится по формуле  = =  ; ;
|
64.производные и дифференциалы высших порядков
1.Пусть  задана явно.Производная от данной функции задана явно.Производная от данной функции 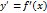 называется производной первого порядка и также является функцией от x.
Производной второго порядка называется производная от производной первого порядка.
Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка. называется производной первого порядка и также является функцией от x.
Производной второго порядка называется производная от производной первого порядка.
Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка.
 2.
2.  – задана неявно. – задана неявно.

 , х-дифференцируем. , х-дифференцируем.

 – дифференцируем по Х. – дифференцируем по Х.
 3.Параметрически.
x=x(t)
y=y(t)
3.Параметрически.
x=x(t)
y=y(t)

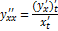 ВОПРОС 69
Вторая производная. Если производная f ' (x) функции f (x) дифференцируема в точке (x 0), то её производная называется второй производной функции f (x) в точке (x 0), и обозначается f '' (x 0).
Функция f (x) называется выпуклой на интервале (a, b), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f (x) в любой точке (x 0, f (x 0)), x 0
ВОПРОС 69
Вторая производная. Если производная f ' (x) функции f (x) дифференцируема в точке (x 0), то её производная называется второй производной функции f (x) в точке (x 0), и обозначается f '' (x 0).
Функция f (x) называется выпуклой на интервале (a, b), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f (x) в любой точке (x 0, f (x 0)), x 0  (a, b).
Функция f (x) называется вогнутой на интервале (a, b), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f (x) в любой точке (x 0, f (x 0)), x 0 (a, b).
Функция f (x) называется вогнутой на интервале (a, b), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f (x) в любой точке (x 0, f (x 0)), x 0  (a, b).
Достаточное условие вогнутости (выпуклости) функции.
Пусть функция f (x) дважды дифференцируема (имеет вторую производную) на интервале (a, b), тогда:
если f '' (x) > 0 для любого x (a, b).
Достаточное условие вогнутости (выпуклости) функции.
Пусть функция f (x) дважды дифференцируема (имеет вторую производную) на интервале (a, b), тогда:
если f '' (x) > 0 для любого x  (a, b), то функция f (x) является вогнутой на интервале (a, b);
если f '' (x) < 0 для любого x (a, b), то функция f (x) является вогнутой на интервале (a, b);
если f '' (x) < 0 для любого x  (a, b), то функция f (x) является выпуклой на интервале (a, b).
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкойперегиба. Отсюда следует, что если в точке перегиба x 0 существует вторая производная f '' (x 0), то f '' (x 0) = 0 (a, b), то функция f (x) является выпуклой на интервале (a, b).
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкойперегиба. Отсюда следует, что если в точке перегиба x 0 существует вторая производная f '' (x 0), то f '' (x 0) = 0
| 65.Теоремы Ферма,Ролля,Коши,Лагранжа
Т.Ферма.
Пусть y=f(x) определена на интервале (a,b) и в некоторой точке  (a,b) достигает локального экстремума.
Тогда если в т. (a,b) достигает локального экстремума.
Тогда если в т.  существует конечная производная,то существует конечная производная,то  Т.Ролля:
Пусть y=f(x) непрерывна на [a,b],дифференцируема в каждой точке интервала (a,b) и выполняется соотношение
f(a)=f(b)
Тогда существует хотя бы одна т. с из интервала (a,b),что f’(x) в с =0.
Т.Ролля:
Пусть y=f(x) непрерывна на [a,b],дифференцируема в каждой точке интервала (a,b) и выполняется соотношение
f(a)=f(b)
Тогда существует хотя бы одна т. с из интервала (a,b),что f’(x) в с =0.
 Т.Коши
f(x) и g(x) непрерывна на [a,b] дифференцируема на (a,b) и
Т.Коши
f(x) и g(x) непрерывна на [a,b] дифференцируема на (a,b) и  для всех для всех  тогда на (a,b) найдется такая точка с тогда на (a,b) найдется такая точка с  (a,b), что (a,b), что
 Т.Лагранжа(следствие из Т.Коши)
Пусть f(x) и g(x) непрерывна на [a,b] дифференцируема на (a,b),тогда внутри (a,b) найдется такая т. с
Т.Лагранжа(следствие из Т.Коши)
Пусть f(x) и g(x) непрерывна на [a,b] дифференцируема на (a,b),тогда внутри (a,b) найдется такая т. с  (a,b) что
f(b)-f(a)=f’(c)(b-a)
т.е. (a,b) что
f(b)-f(a)=f’(c)(b-a)
т.е.  с с  (a,b), что хорда АВ параллельна касательной.
Вопросы к экзамену по курсу "Математика" (I курс, I семестр)
1 Определение матрицы. Виды матриц. Линейные операции над матрицами
2 Произведения матриц. Свойства.
3 Теорема о разложении определителя по элементам ряда (на примере определителя 4 его порядка).
4 Свойства определителей.
5 Определение обратной матрицы и критерий существования обратной матрицы
6. Теорема о существовании единственной обратной матрицы
7. Определение системы линейных уравнений, запись в матричном виде Решение систем
8 Решение невырожденных систем линейных уравнений матричный метод и метод Крамера.
9 Определение ранга матрицы Методы нахождения ранга
10 Теорема Кренекера-Капелли. Правило решения произвольных линейных систем
11. Системы однородных линейных уравнений.
12 Межотраслевой баланс Технологическая матрица
13 Уравнение Леонтьева Критерий продуктивности матрицы.
14 Понятие вектора. Линейные операции над векторами.
15 Понятие базиса. Теорема о разложении вектора по базисным векторам в R3.
16 Скалярное произведение векторов: определение, свойства и приложения.
17. Векторное произведение векторов: определение, свойства и приложения.
18 Смешанное произведение векторов определение, свойства, приложения.
19. Различные формы уравнения прямой на плоскости.
20 Взаимное расположение прямых на плоскости
21 Расстояние от точки до прямой на плоскости (вывод).
22 Окружность - определение, каноническое уравнение, запись в полярных координатах
23. Эллипс-определение, вывод канонического уравнения
24. Основные характеристики эллипса. Теорема (второе определение эллипса)
25. Гипербола - определение, вывод канонического уравнения
26. Основные характеристики гиперболы.
27. Парабола -определение, вывод канонического уравнения.
28 Различные виды уравнений плоскости в пространстве.
29 Расстояние от точки до плоскости. Взаимное расположение плоскостей
30. Виды уравнений прямой в пространстве.
31 Взаимное расположение прямой и плоскости
32 Расстояние от точки до прямой в пространстве
33 Понятие скрещивающихся прямых Расстояние между скрещивающимися прямыми
34. Понятие функции, способы задания, основные элементарные функции.
35. Основные характеристики функций (a,b), что хорда АВ параллельна касательной.
Вопросы к экзамену по курсу "Математика" (I курс, I семестр)
1 Определение матрицы. Виды матриц. Линейные операции над матрицами
2 Произведения матриц. Свойства.
3 Теорема о разложении определителя по элементам ряда (на примере определителя 4 его порядка).
4 Свойства определителей.
5 Определение обратной матрицы и критерий существования обратной матрицы
6. Теорема о существовании единственной обратной матрицы
7. Определение системы линейных уравнений, запись в матричном виде Решение систем
8 Решение невырожденных систем линейных уравнений матричный метод и метод Крамера.
9 Определение ранга матрицы Методы нахождения ранга
10 Теорема Кренекера-Капелли. Правило решения произвольных линейных систем
11. Системы однородных линейных уравнений.
12 Межотраслевой баланс Технологическая матрица
13 Уравнение Леонтьева Критерий продуктивности матрицы.
14 Понятие вектора. Линейные операции над векторами.
15 Понятие базиса. Теорема о разложении вектора по базисным векторам в R3.
16 Скалярное произведение векторов: определение, свойства и приложения.
17. Векторное произведение векторов: определение, свойства и приложения.
18 Смешанное произведение векторов определение, свойства, приложения.
19. Различные формы уравнения прямой на плоскости.
20 Взаимное расположение прямых на плоскости
21 Расстояние от точки до прямой на плоскости (вывод).
22 Окружность - определение, каноническое уравнение, запись в полярных координатах
23. Эллипс-определение, вывод канонического уравнения
24. Основные характеристики эллипса. Теорема (второе определение эллипса)
25. Гипербола - определение, вывод канонического уравнения
26. Основные характеристики гиперболы.
27. Парабола -определение, вывод канонического уравнения.
28 Различные виды уравнений плоскости в пространстве.
29 Расстояние от точки до плоскости. Взаимное расположение плоскостей
30. Виды уравнений прямой в пространстве.
31 Взаимное расположение прямой и плоскости
32 Расстояние от точки до прямой в пространстве
33 Понятие скрещивающихся прямых Расстояние между скрещивающимися прямыми
34. Понятие функции, способы задания, основные элементарные функции.
35. Основные характеристики функций
| 66.Правило Лопиталя
Данное правило применяется при вычислении пределов с неопределенностями  Т.1.(правило Лопиталя
Т.1.(правило Лопиталя  )
Пусть f(x) и g(x) непрерывны на [a,b],дифференцируемы на (a,b) и существует О( )
Пусть f(x) и g(x) непрерывны на [a,b],дифференцируемы на (a,b) и существует О( ), за исключением быть может самой этой точки.
Предположим,что ), за исключением быть может самой этой точки.
Предположим,что  , ,  в О( в О( ) тогда если ) тогда если  Доказательство
Определим f(x) и g(x) в т.
Доказательство
Определим f(x) и g(x) в т.  )=0,тогда эти функции будут непрерывны в т. )=0,тогда эти функции будут непрерывны в т.  и по Т.Коши на [ и по Т.Коши на [ 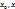 ] будет выполняется неравенство. ] будет выполняется неравенство.

 Т.2(Правило Лопиталя
Т.2(Правило Лопиталя  )
Пусть f(x) и g(x) непрерывны и дифференцируемы в О( )
Пусть f(x) и g(x) непрерывны и дифференцируемы в О( ) и ) и  Тогда если существует
Тогда если существует  , то существует , то существует  и и
 Замечания
1.Правило Лопиталя можно применять неоднократно.
2.В случае неопределенности
Замечания
1.Правило Лопиталя можно применять неоднократно.
2.В случае неопределенности  сначала сводятся к одной из неопределенностей сначала сводятся к одной из неопределенностей  и применяется правило Лопиталя.
36 Понятие обратной и сложной функций.
37. Определение числовой последовательности и ее предела.
38 Теорема о пределе ограниченной последовательности. Определение верхней и нижней грани последовательности.
39 Теорема Вейерштрасса.
40 Вывод числа е
41 Определение предела функции в точке, геометрический смысл предела.
42. Определение односторонних пределов функции в точке. Предел на бесконечности.
43. Определение бесконечно больших и бесконечно малых функций Теорема об алгебраической сумме б.м.ф
44. Основные теоремы о б.м.ф. (одна с доказательством).
45. Теорема (о единственности предела функции в точке).
46 Теорема (основные операции над пределами).
47 Признаки существования предела функции в точке.
48. Замечательные пределы
49. Сравнение б.м.ф. Теорема об эквивалентныхб.м.ф.
50. Три определения непрерывности функции в точке.
51 Основные теоремы о непрерывных функциях
52 Классификация точек разрыва.
53 Свойства функций, непрерывных на отрезке.
54 Определение комплексного числа, основные обозначения, алгебраическая форма.
55 Тригонометрическая форма комплексного числа, изображение на плоскости
56. Формула Муавра и формула корня п - ой степени для комплексного числа.
57. Комплексное число в показательной форме Формула Эйлера Действия над комплексными числами в показательной форме.
58. Определение производной функции в точке. Геометрический и механический смысл производной
59. Экономический смысл производной. Эластичность функции и ее свойства.
60. Основные правила дифференцирования
61 Таблица основных производных
62. Логарифмическая производная. Дифференцирование функций, заданных неявно и параметрически.
63. Дифференциал функции; его геометрический смысл. Применение дифференциала к
приближенным вычислениям
64 Производные и дифференциалы высших порядков
65. Теоремы Ферма, Роля, Коши, Лагргнжа.
66. Правило Лопиталя
67 Условия монотонности функции Экстремум функции: необходимое условие, достаточные условия.
68 Наибольшее и наименьшее значение функции на отрезке.
69 Выпуклость вогнутость графика функции. Точки перегиба.
70 Асимптоты графика функции. Общая схема исследования функции и применяется правило Лопиталя.
36 Понятие обратной и сложной функций.
37. Определение числовой последовательности и ее предела.
38 Теорема о пределе ограниченной последовательности. Определение верхней и нижней грани последовательности.
39 Теорема Вейерштрасса.
40 Вывод числа е
41 Определение предела функции в точке, геометрический смысл предела.
42. Определение односторонних пределов функции в точке. Предел на бесконечности.
43. Определение бесконечно больших и бесконечно малых функций Теорема об алгебраической сумме б.м.ф
44. Основные теоремы о б.м.ф. (одна с доказательством).
45. Теорема (о единственности предела функции в точке).
46 Теорема (основные операции над пределами).
47 Признаки существования предела функции в точке.
48. Замечательные пределы
49. Сравнение б.м.ф. Теорема об эквивалентныхб.м.ф.
50. Три определения непрерывности функции в точке.
51 Основные теоремы о непрерывных функциях
52 Классификация точек разрыва.
53 Свойства функций, непрерывных на отрезке.
54 Определение комплексного числа, основные обозначения, алгебраическая форма.
55 Тригонометрическая форма комплексного числа, изображение на плоскости
56. Формула Муавра и формула корня п - ой степени для комплексного числа.
57. Комплексное число в показательной форме Формула Эйлера Действия над комплексными числами в показательной форме.
58. Определение производной функции в точке. Геометрический и механический смысл производной
59. Экономический смысл производной. Эластичность функции и ее свойства.
60. Основные правила дифференцирования
61 Таблица основных производных
62. Логарифмическая производная. Дифференцирование функций, заданных неявно и параметрически.
63. Дифференциал функции; его геометрический смысл. Применение дифференциала к
приближенным вычислениям
64 Производные и дифференциалы высших порядков
65. Теоремы Ферма, Роля, Коши, Лагргнжа.
66. Правило Лопиталя
67 Условия монотонности функции Экстремум функции: необходимое условие, достаточные условия.
68 Наибольшее и наименьшее значение функции на отрезке.
69 Выпуклость вогнутость графика функции. Точки перегиба.
70 Асимптоты графика функции. Общая схема исследования функции
|
67.условия монотонности функции. экстремум функции:необходимое условие, достаточное условие
Т.1 (необходимое условие  функции)
Если дифференцируемая на (a,b) функция f(x) возрастает(убывает) на (a,b),то функции)
Если дифференцируемая на (a,b) функция f(x) возрастает(убывает) на (a,b),то  2.(достаточное условие
2.(достаточное условие  функции)
Если функция y=f(x) дифференцируема на (a,b) и функции)
Если функция y=f(x) дифференцируема на (a,b) и  , то , то  Т.3 (необходимое условие экстремума)
Если дифференцируемая функция y=f(x) имеет экстремум в т.
Т.3 (необходимое условие экстремума)
Если дифференцируемая функция y=f(x) имеет экстремум в т.  т.е. производная в этой точке равна 0. т.е. производная в этой точке равна 0.
 4(первое достаточное условие экстремума)
Если непрерывная функция y=f(x) дифференцируема в
4(первое достаточное условие экстремума)
Если непрерывная функция y=f(x) дифференцируема в  и при переходе через нее ( и при переходе через нее ( ))
меняет знак с «+» на «-»,тогда ))
меняет знак с «+» на «-»,тогда  -max,если с «-» на «+» -max,если с «-» на «+»  -min
Т.(второе достаточное условие экстремума)
Если -min
Т.(второе достаточное условие экстремума)
Если  т т 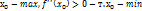 ВОПРОС 70
Асимптоты графика функций
при исследовании графика функции на бесконечность, т.е. при x®+¥ и x®-¥, а так же вблизи точек разрыва часто оказывается, что график сколь угодно близко приближается к той или иной прямой, т.е. асимптоте.
Прямая х=х0 – вертикальная асимптота графика функции y=f(x), если хотя бы один из пределов или равен ± ¥. Нахождение вертикальных асимптот: 1) точки разрыва и граничные точки на области определения 2) вычисляем односторонний предел при х стремящимся к этим точкам.
Прямая y=a – горизонтальная асимптота графика y=f(x), при х®±¥, если.
Прямая y=kx+b называется наклонной асимптотой к графику y=f(x) при х®±¥, если саму функцию y=f(x) можно представить в виде f(x)=kx+b+a(x), где.
Схема нахождения: вычисляем, если этот предел не существует или равен бесконечности, то функция не имеет наклонной асимптоты. Вычисляем, если его нет или он бесконечен, то асимптоты нет.
Схема исследования функции и исследование её графика
1. Область определения функции, промежутки непрерывности, точки разрыва, вертикальные асимптоты
2. точки пересечения с осями.
3. чётность/нечётность
4. периодичность
5. промежутки монотонности и экстремумы
6. Выпуклости, точки перегиба
7. наклонные асимптоты
ВОПРОС 70
Асимптоты графика функций
при исследовании графика функции на бесконечность, т.е. при x®+¥ и x®-¥, а так же вблизи точек разрыва часто оказывается, что график сколь угодно близко приближается к той или иной прямой, т.е. асимптоте.
Прямая х=х0 – вертикальная асимптота графика функции y=f(x), если хотя бы один из пределов или равен ± ¥. Нахождение вертикальных асимптот: 1) точки разрыва и граничные точки на области определения 2) вычисляем односторонний предел при х стремящимся к этим точкам.
Прямая y=a – горизонтальная асимптота графика y=f(x), при х®±¥, если.
Прямая y=kx+b называется наклонной асимптотой к графику y=f(x) при х®±¥, если саму функцию y=f(x) можно представить в виде f(x)=kx+b+a(x), где.
Схема нахождения: вычисляем, если этот предел не существует или равен бесконечности, то функция не имеет наклонной асимптоты. Вычисляем, если его нет или он бесконечен, то асимптоты нет.
Схема исследования функции и исследование её графика
1. Область определения функции, промежутки непрерывности, точки разрыва, вертикальные асимптоты
2. точки пересечения с осями.
3. чётность/нечётность
4. периодичность
5. промежутки монотонности и экстремумы
6. Выпуклости, точки перегиба
7. наклонные асимптоты
| 68.Наибольшее и наименьшее значение функции на отрезке называется глобальным экстремумом.
1.Находим точки возможного локального экстремума( ) и вычисляем значение функции в этих точках.
2.вычисляем значение функции на концах отрезка
Сравниваем полученные значения и вбираем наибольшее и ) и вычисляем значение функции в этих точках.
2.вычисляем значение функции на концах отрезка
Сравниваем полученные значения и вбираем наибольшее и
|
|
|
|
|
|
|
|
| Поделиться: |
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд