Лекция 5.
Линейная алгебра.
Матричное исчисление.
Определение. Матрицей размера 
, где 
число строк, 
число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются 
, где 
номер строки, а 
номер столбца.
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк 
, то матрица называется квадратной.
Определение. Матрица вида:
,
называется единичной матрицей.
Определение. Если 
, то матрица называется симметрической.
Пример.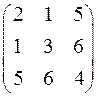 
- симметрическая матрица
Определение. Квадратная матрица вида 
называется диагональной матрицей.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц 
и 
является матрица 
C, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
Пример. Даны матрицы 
; 
, найти 
.
, 
.
Операция умножения матриц.
Определение: Произведением матриц 
и 
называется матрица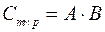 
, элементы которой вычисляются следующим образом:
|
|
.
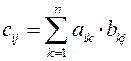Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй: 
.
Свойства операции умножения матриц.
1) Умножение матриц не коммутативно, т.е. 
даже если определены оба произведения. Однако, если для каких – либо матриц соотношение 
выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
Очевидно, что для любых матриц выполняются следующее свойство:
,
где 
нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения 
и 
, то определены 
и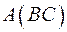 
, и выполняется равенство:
.
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения 
и 
, то соответственно:
4) Если произведение определено, то для любого числа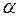 
верно соотношение:
.
5) Если определено произведение АВ, то определено произведение ВТАТ и выполняется равенство:
,
где индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц
.
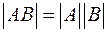Понятие 
определителя матрицы будет рассмотрено ниже.
Определение. Матрицу называют транспонированной матрицей , а переход от к транспонированием, если элементы каждой строки матрицы записать в том же порядке в столбцы матрицы .
|
|
; 
;
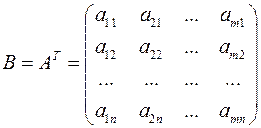другими словами,
.
В качестве следствия из предыдущего свойства (5) можно записать, что:
,
при условии, что определено произведение матриц 
.
Пример. Даны матрицы 
, 
, 
и число 
. Найти 
.
; 
× 
;
; 
.
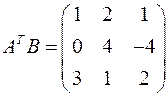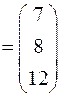Пример. Найти произведение матриц 
и 
.
.
.
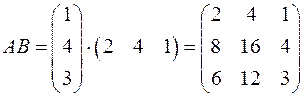Пример. Найти произведение матриц 
, 
