Задание 1 № 77352
При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
Решение.
С учетом комиссии, Аня должна внести в приемное устройство сумму не менее 300 + 300 · 0,05 = 315 рублей. Значит, минимальная сумма, которую должна положить Аня, — 320 рублей. Проверим, что этой суммы достаточно: 5% от нее составляют 16 руб. (это комиссия), оставшиеся 304 рубля пойдут на счет телефона.
Ответ: 320.
Примечание.
Заметим, что сделанная проверка является важной частью решения. Например, если бы Аня хотела бы положить на счет своего телефона 400 руб., она должна была бы сначала вставить в банкомат 400 + 20 = 420 руб., увидеть, что комиссия составляет 21 руб., а на счет телефона поступит 399 руб., и добавить еще 10 руб. Всего 430 руб.
Приведем другое решение.
После уплаты 5% комиссии на счет телефона остаётся 95% вносимой суммы, которая должна быть не меньше 300 рублей. Если нужно внести x рублей, то 0,95 x ≥ 300, откуда x ≥ 315,7... Поэтому x = 320 руб.
Задание 2 № 509828
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа в Томске впервые выпало ровно 1,5 миллиметра осадков.

Решение.
Из графика видно, что впервые 1,5 мм осадков выпало 9 января.
Ответ: 9.
Задание 3 № 27551

Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.

Площадь квадрата равна разности площади прямоугольника и четырех равных прямоугольных треугольников, гипотенузы которых являются сторонами исходного квадрата. Поэтому
 см2.
см2.
Ответ: 10.
Задание 4 № 508961
В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру дня кофе останется в обоих автоматах.
Решение.
Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Тогда
A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,25; P(A·B) = 0,15.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,25 + 0,25 − 0,15 = 0,35.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,35 = 0,65.
Ответ: 0,65.
Приведем другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,25 = 0,75. Вероятность того, что кофе останется во втором автомате равна 1 − 0,25 = 0,75. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,15 = 0,85. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,85 = 0,75 + 0,75 − х, откуда искомая вероятость х = 0,65.
Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,25·0,25 = 0,0625, однако, по условию, эта вероятность равна 0,15.
Задание 5 № 77368
Решите уравнение 
Решение.
Выполним преобразования, используя формулы  :
:

Ответ: −1,5.
Задание 6 № 52003

Угол между хордой AB и касательной BC к окружности равен  Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Решение.
Угол между касательной и хордой равен половине дуги, заключённой между ними. Значит, искомая величина дуги равна 34°.
Ответ: 34.
Задание 7 № 519803

На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  Найдите значение производной функции
Найдите значение производной функции  в
в
точке 
Решение.
По определению, значение производной в точке  равна тангенсу угла наклона касательной, проведенной через данную точку. Таким образом, тангенс равен
равна тангенсу угла наклона касательной, проведенной через данную точку. Таким образом, тангенс равен 
Ответ: 0,25.
Задание 8 № 269541

Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 5.
Решение.
Площадь лежащего в основании пирамиды многоугольника является разностью площадей прямоугольников со сторонами 7, 3 и 6, 2 соответственно (см. рис.):

Поскольку высота пирамиды равна 5, имеем:

Ответ: 15.
Задание 9 № 69201
Найдите значение выражения 
Решение.
Выполним преобразования:

Ответ: 0.
Задание 10 № 28609
Трактор тащит сани с силой 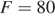 кН, направленной под острым углом
кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной
к горизонту. Работа трактора (в килоджоулях) на участке длиной  м вычисляется по формуле
м вычисляется по формуле  При каком максимальном угле
При каком максимальном угле  (в градусах) совершeнная работа будет не менее 2000 кДж?
(в градусах) совершeнная работа будет не менее 2000 кДж?
Решение.
Задача сводится к решению неравенства  на интервале
на интервале  при заданных значениях силы
при заданных значениях силы  кН и длины пути
кН и длины пути  м:
м:

Ответ: 60.
Задание 11 № 323854
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Решение.
Пусть производительность каждого из рабочих равна  дома в день, и пусть в новом составе бригады достраивали дома
дома в день, и пусть в новом составе бригады достраивали дома  дней. Тогда за первые 7 дней работы бригадами в 16 и 25 человек было построено
дней. Тогда за первые 7 дней работы бригадами в 16 и 25 человек было построено  и
и  частей домов, а за следующие
частей домов, а за следующие 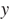 дней бригадами в 24 человека и 17 человек были построены оставшиеся
дней бригадами в 24 человека и 17 человек были построены оставшиеся  и
и  части домов. Поскольку в результате были целиком построены два дома, имеем:
части домов. Поскольку в результате были целиком построены два дома, имеем:

Значит, в новом составе бригады работали 9 дней. Таким образом, потребовалось 7 + 9 = 16 дней на выполнений заказов.
Ответ: 16.
Задание 12 № 128997
Найдите точку минимума функции 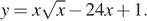
Решение.
Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума 
Ответ: 256.
Задание 13 № 484547
Решите уравнение 
Решение.
 Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю и не теряет смысла. Поэтому данное уравнение равносильно системе:
Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю и не теряет смысла. Поэтому данное уравнение равносильно системе:

Решив уравнение системы как квадратное относительно  находим
находим  либо
либо  Если
Если  то
то  то есть
то есть  Следовательно,
Следовательно, 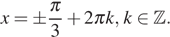 Если
Если  то
то  В этом случае с учетом условия
В этом случае с учетом условия  системы получаем, что из двух точек единичной окружности, соответствующих решениям уравнения
системы получаем, что из двух точек единичной окружности, соответствующих решениям уравнения  нужно оставить только ту, для которой
нужно оставить только ту, для которой  Это точка четвертой четверти, и решение уравнении имеет вид
Это точка четвертой четверти, и решение уравнении имеет вид 
Ответ: 
Задание 14 № 509821
Основанием прямой четырехугольной призмы ABCDA'B'C'D' является квадрат ABCD со стороной 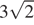 , высота призмы равна
, высота призмы равна  Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Решение.

а) Проведём KE — среднюю линию треугольника BB'D'. E — середина B'D', следовательно, точка пересечения диагоналей верхнего основания и сечение содержит диагональ A'C'. Треугольник A'C'K является искомым сечением по признаку параллельности прямой и плоскости.
Прямоугольные треугольники A'B'K и С'B'K равны по двум катетам, поэтому A'K = С'K, следовательно, треугольник A'C'K — равнобедренный.
б) Далее имеем:




Ответ: б) 16.
Задание 15 № 508448
Решите неравенство: 
Решение.
Сделаем замену 

Возвращаясь к исходной переменной, получим:  или
или 
Ответ: 
Задание 16 № 505431
Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.
а) Докажите, что треугольник BCK — равнобедренный.
б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если 
Решение.

а) Угол KBC равен углу BAC как угол между касательной и хордой. Прямые AB и CK параллельны. Следовательно, ∠ ABC = ∠ BCK. Получаем, что треугольники ABC и BCK подобны. Следовательно,

Значит, треугольник BCK — равнобедренный.
б) Треугольники ABC и BCK подобны, коэффициент подобия равен  Отношение площадей
Отношение площадей  В треугольнике ABC имеем:
В треугольнике ABC имеем:


Ответ: 2.
Задание 17 № 507212
31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Пусть сумма кредита равна  а годовые составляют
а годовые составляют  Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент
Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент  После первой выплаты сумма долга составит
После первой выплаты сумма долга составит  После второй выплаты сумма долга составит
После второй выплаты сумма долга составит

После третьей выплаты сумма оставшегося долга равна

После четвертой выплаты сумма оставшегося долга равна

По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому

При  и
и  получаем:
получаем:  и
и

Ответ: 2 296 350.
Задание 18 № 522127
Найдите все значения a, при которых уравнение

имеет единственное решение на отрезке [-1; 1].
Решение.
Уравнение  равносильно уравнениям
равносильно уравнениям 
 и
и  Положим
Положим 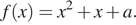 Последнее уравнение имеет единственный корень на отрезке
Последнее уравнение имеет единственный корень на отрезке 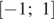 тогда и только тогда, когда выполнен один из трёх случаев: либо квадратный трёхчлен
тогда и только тогда, когда выполнен один из трёх случаев: либо квадратный трёхчлен  имеет единственный корень и этот корень принадлежит интервалу
имеет единственный корень и этот корень принадлежит интервалу  либо
либо  имеет единственный корень на отрезке
имеет единственный корень на отрезке  равный −1 или 1, либо квадратный трёхчлен
равный −1 или 1, либо квадратный трёхчлен  принимает при
принимает при  и
и  ненулевые значения разных знаков.
ненулевые значения разных знаков.
Рассмотрим первый случай. Квадратный трёхчлен  имеет единственный корень при равенстве нулю его дискриминанта, то есть при
имеет единственный корень при равенстве нулю его дискриминанта, то есть при  или, что то же самое, при
или, что то же самое, при 
При таком значении  уравнение
уравнение  имеет единственный корень
имеет единственный корень  он принадлежит отрезку
он принадлежит отрезку 
Рассмотрим второй случай. Имеем  и
и  Значит,
Значит,  при
при  При таком значении
При таком значении  уравнение
уравнение  имеет два решения
имеет два решения  и
и  на отрезке
на отрезке  Аналогично
Аналогично  при
при  При таком значении
При таком значении  уравнение
уравнение  имеет единственное решение
имеет единственное решение  на отрезке
на отрезке 
Рассмотрим третий случай. Значения  и
и  имеют разные знаки тогда и только тогда, когда
имеют разные знаки тогда и только тогда, когда  или, что то же самое, при
или, что то же самое, при 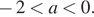
Следовательно, уравнение  имеет единственное решение на отрезке
имеет единственное решение на отрезке  тогда и только тогда, когда a=0,25 или -2\le a<0.
тогда и только тогда, когда a=0,25 или -2\le a<0.
Ответ: 
Задание 19 № 500966
Имеется 8 карточек. На них записывают по одному каждое из чисел:
−11, 12, 13, −14, −15, 17, −18, 19.
Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному из чисел:
−11, 12, 13, −14, −15, 17, −18, 19.
После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 117?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Решение.
а) Среди восьми данных чисел нет противоположных. Значит, сумма чисел на каждой карточке не равна 0. Поэтому всё произведение не может равняться 0.
б) Среди восьми данных чисел пять нечётных. Значит, на какой-то карточке попадётся два нечётных числа, и их сумма чётная. Поэтому всё произведение чётно и не может равняться 117.
в) Среди восьми данных чисел пять нечётных. Значит, хотя бы на двух карточках с обеих сторон написаны нечётные числа, и сумма чисел на каждой из этих карточек чётная. Поэтому все произведение делится на 4. Наименьшее целое положительное число, делящееся на 4, это 4. Оно получается при следующем наборе пар чисел на карточках:
(−11; 12), (12; −11), (13; −14), (−14; 13),(−15; 17), (17; −15), (−18; 19), (19; −18),
Ответ: а) нет; б) нет; в) 4.