| Две прямые, лежащие в одной плоскости образуют четыре неразвёрнутых угла острый угол α называется углом между пересекающимися прямыми a и b | На экране изображение с постепенным появлением отметок углов и обозначением
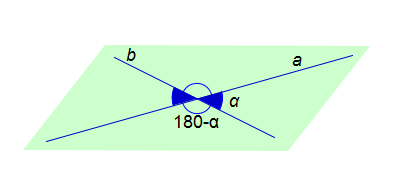 На фоне рисунка появляется надпись
a^b=α, где 0° <α≤90°
На фоне рисунка появляется надпись
a^b=α, где 0° <α≤90°
| ||||||||||||
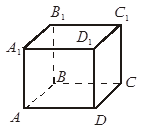
| Рассмотри известную нам фигуру параллелепипед Все его грани являются прямоугольниками, что доказывает что угол между прямыми АА1 и АВ равен 90 градусов. Такие прямые в пространстве называются перпендикулярными или взаимно перпендикулярными. | На экране изображение
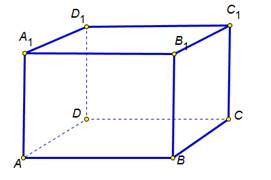 На экране выделяются прямые АА1 и АВ
На экране определение:
Две прямые в пространстве называются перпендикулярными, если угол между ними 90°.
На экране выделяются прямые АА1 и АВ
На экране определение:
Две прямые в пространстве называются перпендикулярными, если угол между ними 90°.
| ||||||||||||
| Таким образом, на данном рисунке DD1 и D1C1 взаимно перпендикулярные прямые. Перпендикулярность прямых DD1 и D1C1 обозначается так. | На экране изображение
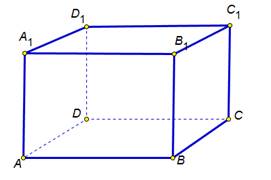 На экране изображение
DD1
На экране изображение
DD1 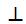 D1C1 D1C1
| ||||||||||||
| Рассмотрим модель куба. Известно, что его грани это квадраты, следовательно, прямые AA1, АD перпендикулярные прямые. Справедливы и другие утверждения: Прямая DD1 перпендикулярна прямой АD. Прямая АА1 параллельна прямой DD1. Совсем не случайно каждая из двух параллельных прямых оказалась перпендикулярна прямой АD. | На экране изображение (желательно анимировать проговариваемые прямые одновременно):
На экране обновляется изображение с анимацией.
| ||||||||||||
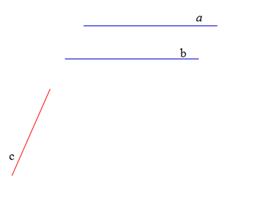
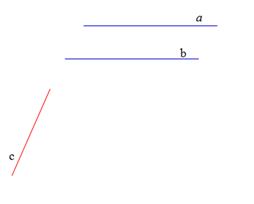
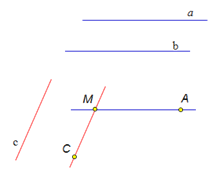
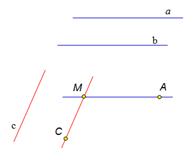
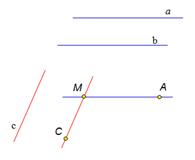
| Данная конфигурация рисунка соответствуют известной в геометрии лемме о перпендикулярности двух параллельных прямых к третьей прямой. Докажем её. Рассмотрим параллельные прямые а и b перпендикулярные прямые а и c. Докажем, что прямая b перпендикулярна прямой с. Для доказательства через произвольную точку пространства проведем прямые МА и МС, такие, что прямая МА параллельна прямой а и прямая МС параллельна прямой с. Так как прямые а и с перпендикулярны, то угол АМС равен 90 градусов. Так как прямая b параллельна прямой а по условию, а прямая а параллельна прямой МА по построению, следовательно, прямая b параллельна прямой МА. Итак, прямая b параллельна прямой МА, а прямая с параллельна прямой МС. Прямые МА и МС взаимно перпендикулярные прямые, следовательно, прямая b перпендикулярна прямой с. Лемма доказана. |
На экране текст:
Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
На экране изображение и текст:
На экране соответствующие тексту автора изменения
На экране последовательные изменения соответственно тексту:
На экране соответствующие изменения изображения и текста
На экране соответствующие изменения изображения и текста
На экране соответствующие изменения изображения и текста
| ||||||||||||
| Доказанная лемма упрощает решение задач и доказательство теорем. Рассмотрим один из примеров. | |||||||||||||
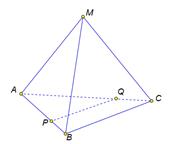
В тетраэдре МАВС ребра МА и ВС перпендикулярны, Р - точка ребра АВ, причём АР относится к АВ как 2 к 3. Q-точка ребра АС, причём АQ относиться к QC, как 2 к 1.
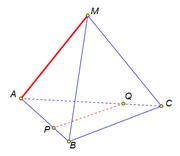
Доказать, что прямая АМ перпендикулярна прямой PQ.
Для доказательства рассмотрим два треугольника APQ и АВС с общим углом А.
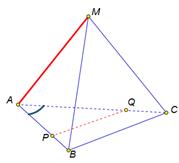
Так как Точка Q делит сторону АC в отношении 2 к 1, то сторона АQ треугольника АРQ составляет  стороны АС треугольника АВС. Таким образом в треугольниках АРQ и АВС сторона АР относиться стороне АВ как 2 к 3, сторона АQ относиться к стороне АС как 2 к 3 и угол А у них общий, значит треугольник APQ подобен треугольнику АВС.
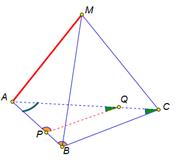
Из подобия треугольников следует равенство соответственных углов APQ и АВС, АQР и АСВ, это доказывает параллельность прямых РQ и ВС.
Итак прямая АМ перпендикулярна прямой ВС, а прямая PQ параллельна прямой ВС, тогда согласно доказанной лемме АМ перпендикулярна прямой PQ. стороны АС треугольника АВС. Таким образом в треугольниках АРQ и АВС сторона АР относиться стороне АВ как 2 к 3, сторона АQ относиться к стороне АС как 2 к 3 и угол А у них общий, значит треугольник APQ подобен треугольнику АВС.
Из подобия треугольников следует равенство соответственных углов APQ и АВС, АQР и АСВ, это доказывает параллельность прямых РQ и ВС.
Итак прямая АМ перпендикулярна прямой ВС, а прямая PQ параллельна прямой ВС, тогда согласно доказанной лемме АМ перпендикулярна прямой PQ.
| На экране изображение и текст
На экране изменяется изображение и текст с выделением прямых
На экране обновляется рисунок и текст под слова автора.
|
Комментарий: сценарий написан очень хорошо подробно разобрано задание, профессионально разобраны этапы доказательства леммы и задачи.





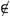 a, М
a, М 


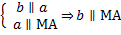
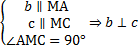
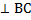 Р∈АВ, Q∈АС, АР:АВ=2:3, АQ:QC=2:1
Р∈АВ, Q∈АС, АР:АВ=2:3, АQ:QC=2:1
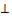 PQ
PQ
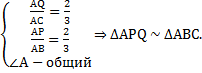
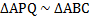 , то
∠ АРQ = ∠ А ВС, ∠ АQР = ∠ АСВ, значит по признаку параллельных прямых РQ ∥ВС.
, то
∠ АРQ = ∠ А ВС, ∠ АQР = ∠ АСВ, значит по признаку параллельных прямых РQ ∥ВС.

