1. Даны числа a, b, c. Найти максимальное.
2. Даны числа a, b, c. Найти минимальное.
3. Даны числа a, b, c. Найти среднее.
4. Даны числа a, b, c. Выбрать из них те, которые принадлежат интервалу (d, l).
5. Даны числа a, b, c. Каждое число заменить наибольшим, если числа образуют возрастающую последовательность. В остальных случаях числа оставить без изменений.
6. Даны числа a, b, c. Каждое число заменить наименьшим, если числа образуют убывающую последовательность. В остальных случаях числа оставить без изменений.
7. Даны числа a, b, c. Существует ли треугольник с длинами сторон a, b, c?
8. Даны числа a, b, c. Выяснить, имеет ли квадратное уравнение 
действительные корни. Если имеет, то найти их.
9. Даны числа a, b, c. Исследовать биквадратное уравнение 
на наличие действительных корней и найти их.
10. Выяснить, можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонами c, d.
11. Дать ответ на вопрос: пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x, y.
12. Определить, является ли треугольник с координатами вершин (x 1, y 1), (x 2, y 2), (x 3, y 3) прямоугольным.
13. Выяснить, является ли четырехугольник с координатами вершин (x 1, y 1), (x 2, y 2), (x 3, y 3), (x 4, y 4) квадратом.
14. Выяснить, является ли четырехугольник с координатами вершин (x 1, y 1), (x 2, y 2), (x 3, y 3), (x 4, y 4) ромбом.
15. Выяснить, является ли четырехугольник с координатами вершин (x 1, y 1), (x 2, y 2), (x 3, y 3), (x 4, y 4) прямоугольником.
16. Даны три числа x, y, z. Если их сумма меньше 1, то наименьшее заменить полусуммой двух других, иначе наименьшее заменить наибольшим.
17. Даны три числа x, y, z. Если их сумма больше 1, то наибольшее из x и y заменить полусуммой оставшихся, иначе наибольшее из трех чисел заменить наименьшим.
18. Можно ли построить четырехугольник со сторонами a, b, c, d?
19. Для заданных значений a, b, c найти 
.
20. Даны четыре неравных числа a, b, c, d. Определить среднее значение двух чисел, которые не являются минимумом и максимумом.
21. Заданы три числа x, y, z. Если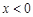 
, то p задать как максимальное из y и z.
22. Заданы три числа x, y, z. Если 
, то p задать как минимальное из x и y.
23. Произвольный выпуклый четырехугольник задан координатами своих вершин на плоскости. Есть ли в этом четырехугольнике прямые углы?
24. Заданы три числа a, b, c. Если 
, то определить p как минимальное из b и c, иначе вычислить p как среднее арифметическое из b и c.
25. Заданы три числа a, b, c. Если 
, то p задать как максимальное из b и c, иначе вычислить p как среднее арифметическое из a, b и c.
26. Заданы три числа a, b, c. Если 
, то вычислить p как среднее арифметическое от b и c, иначе минимальное из трех чисел заменить максимальным.
27. Даны две окружности радиусом R 1 и R 2 с центром в начале координат. Определить, где находится точка с координатами (x, y): внутри меньшей окружности, в кольце между окружностями или вне их.
28. Заданы координаты двух точек. Определить, лежат ли они на одной окружности с центром в начале координат.
29. Заданы площади круга S 1 и квадрата S 2. Выяснить, поместится ли круг в квадрате.
30. Заданы площади круга S 1 и квадрата S 2. Выяснить, поместится ли квадрат в круге.
Лабораторная работа № 3
Программирование циклических
вычислительных процессов
Цель работы. Получить навыки программирования циклических вычислительных процессов. Изучить циклы с шагом и циклы с условием.
Введение
Работа содержит задачи, которые сводятся к нахождению конечной суммы ряда 
при различных значениях x. Каждое слагаемое 
зависит от величины x и номера n, определяющего место этого слагаемого в сумме. Ряды подобраны таким образом, чтобы при бесконечно большом числе членов ряда их сумма в указанном диапазоне изменения величины x была конечным числом, зависящим только от x, т.е. ряды являются сходящимися. Например,
= 
= 
.
Первый член этого ряда при 
равен 
, второй член при 
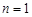равен 
, третий член при 
равен 
и т.д. В сумме при бесконечно большом числе членов они дают функцию 
. Видно, что при ограниченных значениях x, сравнимых по модулю с единицей, каждый последующий член этого знакопеременного ряда существенно меньше предыдущего, поэтому ряд быстро сходится и для вычисления суммы ряда с необходимой точностью достаточно просуммировать относительно небольшое число членов ряда. Например, суммирование можно прекратить, когда текущий член ряда станет по абсолютной величине меньше заданного малого положительного числа 
, определяющего погрешность вычисления суммы ряда.
Формула общего члена суммы принадлежит к одному из следующих типов:
а) 
; 
; 
;
б) 
; 
; 
;
в) 
; 
.
В случае а) для вычисления члена суммы целесообразно использовать рекуррентные соотношения, т.е. выражать последующий член суммы через предыдущий, например, если
, то
.
В случае б) каждый член суммы вычисляется согласно общей формуле, которую и нужно запрограммировать.
В случае в) член суммы целесообразно представить в виде двух переменных, одна из которых вычисляется по рекуррентному соотношению, а другая – непосредственно, например, если
то
, где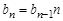 
, 
.
Задание
1. Записать расчетные формулы для вычисления слагаемого и конечной суммы ряда 
. Варианты заданий приведены в табл. 3.
2. Составить алгоритм вычисления с заданной точностью суммы конечного числа членов ряда в указанном диапазоне изменения параметра x с заданным шагом. Для получения шага диапазон изменения x разделить на 10.
3. Составить программу решения задачи. В программе для каждого значения x предусмотреть вычисление как приближенной, так и точной суммы соответствующего ряда y по приведенной в табл. 3 формуле.
4. Отладить программу. Результат получить в виде таблицы, содержащей для каждого x из указанного диапазона приближенное и точное значения суммы ряда, а также количество просуммированных членов.