Лабораторная работа № 1
Табулирование функций
Цель работы. При табулировании и построении графиков функций получить начальные навыки программирования.
Задание
Получить таблицы шести функций, заданных аналитическими выражениями, с помощью языка программирования Фортран (FORTRAN). Используя табличный процессор Microsoft Excel, построить графики функций. Варианты заданий приведены в табл. 1.
Выбор языка программирования Фортран обусловлен тем, что он предназначен для быстрого счета в различных научно-технических приложениях. Именно на решение научно-технических задач нацелена подготовка специалистов на факультете летательных аппаратов.
Введение
Выражение – это формула для получения значения. Выражения образуются из операндов и знаков операций, объединяемых по правилам синтаксиса алгоритмического языка. В качестве операндов выражения используются буквальные и именованные константы, переменные, указатели функций. В зависимости от типа возвращаемого результата выражения подразделяются на арифметические, логические, символьные и производного типа. В первой лабораторной работе рассмотрим правила составления арифметических выражений.
При записи арифметических выражений в Фортране используются следующие арифметические операции (в порядке возрастания приоритета) и функции:
–, + – вычитание и сложение;
*, / – умножение и деление;
** – возведение в степень;
| COS(x) – cos(x) | SIN(x) – sin(x) | TAN(x) – tg(x) |
| COTAN(x) – ctg(x) | ATAN(x) – arctg(x) | SQRT(x) – 
|
| EXP(x) – ex | ALOG(x) – ln(x) | ALOG10(x) – lg(x) |
| ABS(x) – | x | | INT(x) – целая часть x |

Порядок выполнения операций одного и того же приоритета – слева направо (кроме возведения в степень). Для изменения упомянутого выше порядка вычислений используются круглые скобки.
Далее рассмотрим пример выполнения следующего варианта:


Следует остановиться на подготовке исходных данных для программы. Вначале обязательно устанавливают область определения функции. Для 1-й функции областью определения является вся числовая ось от  до
до  . Но вследствие периодичности функции синус достаточно построить график в интервале
. Но вследствие периодичности функции синус достаточно построить график в интервале  или
или  . Видно также, что областью изменения функции является интервал
. Видно также, что областью изменения функции является интервал  . Каждая пара значений x и y должна быть записана в таблицу результатов счета.
. Каждая пара значений x и y должна быть записана в таблицу результатов счета.
Запишем алгоритм решения первой задачи.
1. Зададим тип и значение неизменяемому параметру  .
.
2. Опишем тип используемых в программе переменных.
3. Откроем файл для записи значений x и y.
4. Определим начальное a и конечное b значения переменной x.
5. Введем количество строк n для табулирования функции.
6. Вычислим шаг h цикла для изменения переменной x.
7. Организуем цикл с управляющей переменной i целого типа.
8. В цикле вычислим значения переменных x и y.
9. Напечатаем на дисплей значения x и y.
10. Повторим печать значений x и y в файл.
11. Закончим цикл.
В соответствии с алгоритмом составим Фортран-программу:
PROGRAM LAB1
REAL, PARAMETER:: PI=3.141593
REAL A, B, H, X, Y
INTEGER I, N
OPEN(1, FILE=’LAB1.TXT’)
A=-2./3.; B=2.*(PI-1.)/3.
PRINT *, ’ N=?’; READ *, N
H=(B-A)/N
DO I=0,N
X=A+H*I
Y=0.5*SIN(3.*X+2.)
PRINT 2, X,Y; WRITE(1, 2) X,Y
END DO
2 FORMAT (' X=',F8.4,3X,'Y=',F8.4)
END PROGRAM LAB1
Прокомментируем работу программы:
– вначале после ключевого слова PROGRAM объявляется имя программы, которое обязательно должно начинаться с буквы латинского алфавита или символа $ (в общем случае ключевое слово PROGRAM с именем программы может отсутствовать);
– первый оператор задает тип и значение именованной константе PI;
– затем идут два оператора, описывающие тип используемых в программе переменных;
– оператор OPEN назначает логический номер 1 файлу «LAB1.TXT». Указанный файл создается в папке проекта в процессе работы программы в момент выполнения оператора OPEN;
– в следующей строке через точку с запятой записаны два оператора, которые вычисляют значения переменных A и B (обратите внимание на десятичные точки в неименованных константах вещественного типа);
– оператор PRINT выводит на дисплей в свободном формате символьную константу, которая заключена в апострофы. Эта последовательность символов является подсказкой для пользователя;
– оператор READ требует ввода с клавиатуры значения целой переменной N. После нажатия клавиши [Enter] переменной N будет присвоено набранное значение;
– следующий оператор вычисляет значение переменной H;
– оператор цикла DO организует повторение вычислений в теле цикла необходимое число раз при изменении управляющей переменной I от 0 до N с шагом 1 (шаг равен 1 по умолчанию, так как его значение не указано);
– операторы в следующих двух строках обеспечивают вычисление арифметических выражений, записанных справа от знака равенства. Результаты присваиваются переменным X и Y;
– оператор PRINT работает под управлением оператора FORMAT с меткой 2. Он выводит на экран сначала символьную константу X=, которая в программе заключена в апострофы, затем числовое значение переменной X по дескриптору F8.4. Далее через три позиции выводятся символьная константа Y=, и значение Y также по дескриптору F8.4, где 8 – общее число позиций для выводимого числа, а 4 – количество позиций для цифр после десятичной точки. В общее число позиций включаются знак отрицательного числа «–» и десятичная точка (ноль перед десятичной точкой, как правило, не печатается);
– оператор WRITE повторяет печать значений X и Y в файл «LAB1.TXT» с логическим номером 1 под управлением оператора FORMAT с меткой 2;
– оператор END DO ограничивает тело цикла;
– последний оператор END PROGRAM LAB1 ограничивает программный модуль, заканчивая его (LAB1 или PROGRAM LAB1 могут быть опущены). Если имя программы не объявлено, то оно не может присутствовать и в операторе END.
Краткая инструкция по работе
в среде программирования
Для запуска составленной программы на счет необходимо прежде всего создать проект. Для этого предлагаем использовать среду Developer Studio (мастерскую разработчика), в которой программирование осуществляется на языке Compaq Visual Fortran (CVF) версии 6.1. Для входа в среду Developer Studio необходимо после нажатия кнопки «Пуск» выбрать из меню “Все программы” пункт Compaq Visual Fortran 6 и далее подпункт Developer Studio, либо другим способом – дважды щелкнуть по иконке Developer Studio на рабочем столе.
Далее для создания проекта необходимо выполнить следующую цепочку действий: File – New – выбрать закладку Projects – Fortran Standard Graphics or QuickWin Application – ввести имя проекта – задать расположение проекта на диске. В качестве места расположения проекта студентам рекомендуется использовать папку с именем группы, специально созданную в папке FLA на жестком диске C: компьютера. После нажатия кнопки OK в появившемся окне нужно выбрать кнопку QuickWin (multiple windows) и нажать Finish и еще раз OK. В результате этих действий создается папка с именем проекта. В этой папке будут размещены файлы с расширениями .dsp, .dsw и .opt, фиксирующие структуру проекта. Сам же проект отобразится в окне с закладкой File View. Для сохранения конфигурации проекта можно использовать меню File – Save All. Желательно запомнить имя и расположение проекта для того, чтобы при необходимости можно было найти и открыть созданный проект.
Заметим, что уже существующий проект открывается по цепочке File – Open Workspace– выбор файла с расширением .dsw – Open, а закрывается командами File – Close Workspace.
Создадим теперь файл, в который будет занесен текст программы. Для этого необходимо выполнить действия: File – New – выбрать закладку Files – выбрать Fortran Free Format Source File – активизировать опцию (поставить «галочку») Add to project – задать имя файла – OK. Созданный файл должен иметь расширение .f90. Далее наберем в правом окне текст программы. В процессе набора ключевые слова Фортрана и имена встроенных функций отображаются синим цветом, а комментарии – зеленым. Начальный отступ предыдущей строки наследуется, что облегчает набор структурированных программ в свободном формате. При наборе больших программ желательно периодически сохранять файл, записывая его на диск.
Если же файл с программой уже существует, то для добавления его в проект нужно: в окне FileView – выбрать папку Source Files – нажать на правую кнопку мышки – Add Files to Folder – выбрать тип файлов – выбрать необходимые файлы – OK. Чтобы отобразить на экране содержимое файла, достаточно с помощью левой клавиши мышки дважды щелкнуть по нему в окне File View (в папке Source Files). Можно сначала открыть файл в правом окне Developer Studio, а затем включить его в проект. Для этого при нахождении курсора мышки в правом окне нужно нажать правую клавишу мышки, в появившемся контекстном меню выбрать пункт Insert File into Project и щелкнуть левой клавишей мышки на имени проекта.
Для удаления файла из открытого проекта достаточно выбрать этот файл в окне FileView и нажать клавишу [Del].
Для перевода программы на язык машинного уровня выполним компиляцию проекта с помощью меню Build – Compile и исправим обнаруженные ошибки, сообщения о которых появятся в нижнем окне экрана. При отсутствии ошибок программа переводится с языка Фортран на язык машинного (объектного) уровня и создается объектный модуль с расширением .obj.
Далее, используя меню Build – Build, построим исполняемый файл с расширением .exe, в котором объединяются объектные коды главной программы и вызываемых ею вспомогательных процедур, в том числе встроенных.
Исполняемый файл запустим на счет с помощью меню Build – Execute. Результат выводится в специальное рабочее окно. Отметим, что кириллические тексты на экране воспроизводятся в искаженном виде. Фрагменты содержимого окна результатов можно переносить в другие файлы через буфер обмена. Прекратить счет можно нажатием комбинации клавиш [Ctrl + C]. Если программа закончила работу, то можно выйти из окна сразу и вернуться к программе или поработать с результатами средствами операционной системы Windows и затем закрыть окно.
Компиляцию, построение исполняемого модуля и запуск программы можно также выполнить с помощью кнопок панели инструментов или клавишных комбинаций, имеющихся в меню Build.
Получение таблиц остальных заданных функций
Во 2-й задаче область определения функции устанавливается исходя из того, что подкоренное выражение должно быть неотрицательно. Следовательно, 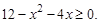 Решая квадратное уравнение, получаем область определения:
Решая квадратное уравнение, получаем область определения:  При исполнении программы все значения аргумента следует брать только из этой области, так как вне ее функция не определена. Следовательно, в программе для 2-й задачи требуется изменить значения переменных A и B в третьей строке, набрав вместо старых операторов новые
При исполнении программы все значения аргумента следует брать только из этой области, так как вне ее функция не определена. Следовательно, в программе для 2-й задачи требуется изменить значения переменных A и B в третьей строке, набрав вместо старых операторов новые
A = – 6.; B = 2.
И в соответствии с заданием изменяется оператор вычисления переменной y:
Y=1.+SQRT(12.-X**2-4.*X)
Указанные изменения в программе лучше оформить в отдельном файле, который можно получить из прежнего, выполнив File – Save As и набрав имя нового файла. Затем следует выполнить удаление из проекта старого файла, включение в проект нового файла, компиляцию, построение загрузочного модуля и запуск программы.
Аналогично проводятся вычисления для 3-й и 4-й функций, для которых также лучше оформить отдельные файлы.
В 5-й задаче функция задается параметрически, поэтому здесь сначала в цикле вычисляется переменная T, соответствующая параметру функции, а затем переменные X и Y. В результате операторы присваивания принимают вид:
T=A+H*I
X=2.*COS(T)*SQRT(ABS(COS(2.*T)))
Y=2.*SIN(T)*SQRT(ABS(COS(2.*T)))
В 6-й задаче функция описывается полярными координатами с радиусом-вектором  из начала декартовых координат и углом
из начала декартовых координат и углом  , который отсчитывается от оси абсцисс против часовой стрелки. Целесообразно перейти от полярных координат к декартовым координатам по формулам:
, который отсчитывается от оси абсцисс против часовой стрелки. Целесообразно перейти от полярных координат к декартовым координатам по формулам:


С использованием переменных  ,
,  для вычисления значений
для вычисления значений  и
и 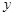 новую программу лучше сделать из предыдущей, в которой следует заменить переменную T на переменную F, а также изменить два оператора присваивания для переменных X, Y и перед ними добавить еще один, соответствующий заданной функции:
новую программу лучше сделать из предыдущей, в которой следует заменить переменную T на переменную F, а также изменить два оператора присваивания для переменных X, Y и перед ними добавить еще один, соответствующий заданной функции:
R=16./(5.-3.*COS(F))
X=R*COS(F); Y=R*SIN(F)
В рассмотренном примере угол  необходимо задавать в интервале от 0 до
необходимо задавать в интервале от 0 до 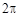 . В общем случае область определения функции находится из условия
. В общем случае область определения функции находится из условия  .
.
Вычисление функций и Построение графиков
в табличном процессоре Microsoft Excel
Перед началом работы необходимо осуществить запуск Excel, щелкнув мышью на кнопке <Пуск> и выполнив команду Все программы / Microsoft Office / Microsoft Office Excel. Пустая электронная таблица, открываемая Excel сразу после его запуска, по умолчанию имеет имя Book1 (Книга1).
Вычисление функций
Ввод данных осуществляется в активную ячейку. Активной называется ячейка, в которой в данный момент времени расположен табличный (или окошечный) курсор. Курсор перемещается с помощью клавиатуры или с помощью мыши. Введите данные в пустую электронную таблицу в следующем порядке.
· Сделайте активной ячейку A1 и введите текст «Функция 1». Обратите внимание, что вводимая информация дублируется в строке формул. Для окончания ввода информации в ячейку необходимо или нажать клавишу Enter, или щелкнуть по галочке слева от строки редактирования, или перевести курсор в другую ячейку. В ячейки С1, С2, С3, С4 ввести соответственно «N», «А», «B», «H». В смежные справа ячейки D1, D2, D3, D4 задать N, начальное, конечное значения переменной x и шаг. В ячейку D4, где вычисляется шаг, следует записать =(D3-D2)/D1.
· Сделайте активной ячейку A2 и введите первое значение x (=D2), затем в активную ячейку A3 – второе значение x (=A2+$D$4).
· Переведите курсор мышки в ячейку B2 и введите в нее первое значение y рассматриваемой функции (например =sin(A2)), затем в ячейку B3 введите второе значение y (=sin(A3)).
· Дальнейшие вычисления можно существенно упростить, поскольку переменная x изменяется с постоянным шагом. Для этого нужно выделить (маркировать) две ячейки A3 и B3, содержащие значения x и y. Выделение осуществляется буксировкой мышки (при нажатой левой клавише) по выбранным ячейкам. Затем нужно отпустить левую клавишу и поместить курсор мышки в правый нижний угол выделенной области так, чтобы появился крестик черного цвета. Далее следует снова нажать левую клавишу мышки и продолжить буксировку вниз до появления крайнего значения x из заданного диапазона, после чего можно отпустить левую клавишу мышки.
Построение графиков
Во-первых, необходимо выделить область таблицы, содержащую данные, по которым нам необходимо построить график. В нашем случае это ячейки, начиная с A2 до B12. Выделение группы ячеек осуществляется буксировкой мышки. Затем нужно использовать команду построения диаграммы «Вставка / Диаграмма» или соответствующую пиктограмму. Далее:
– выбираем тип диаграммы «Точечная» и её вид;
– проверяем диапазон адресов маркированных областей данных;
– вводим название диаграммы и осей;
– выбираем режим «построение диаграммы на имеющемся листе».
При необходимости осуществляется корректировка диаграммы. Для этого нужно активизировать диаграмму щелчком левой кнопки мышки, щелкнуть правой кнопкой мышки в области диаграммы на свободном от её элементов месте и в открывшемся контекстном меню выбрать нужную команду или элемент.
 Сохранение документа на диске
Сохранение документа на диске
 Выполните команду «Файл / Сохранить как». В открывшемся окне в поле ввода «Имя файла» введите название файла «Lab1.xls». Обратите внимание, в какой папке будет сохранен документ (при необходимости откройте другую папку). Наконец, нажмите командную кнопку «Сохранить». Аналогично внесите данные и постройте графики остальных пяти функций на отдельных листах книги Excel. Добавить листы можно с помощью меню Вставка – Лист.
Выполните команду «Файл / Сохранить как». В открывшемся окне в поле ввода «Имя файла» введите название файла «Lab1.xls». Обратите внимание, в какой папке будет сохранен документ (при необходимости откройте другую папку). Наконец, нажмите командную кнопку «Сохранить». Аналогично внесите данные и постройте графики остальных пяти функций на отдельных листах книги Excel. Добавить листы можно с помощью меню Вставка – Лист.
 Таблица 1
Таблица 1
Варианты заданий к лабораторной работе № 1
| № п/п | ||||||

| 
| 
| 
| 
| 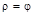
| |

| 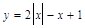
| 
| 
| 
| 
| |

| 
| 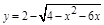
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 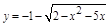
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
|
Продолжение табл. 1
 № п/п № п/п
| ||||||

| 
| 
| 
| 
| 
| |

| 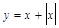
| 
| 
| 
| 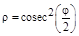
| |

| 
| 
| 
| 
| 
| |

| 
| 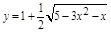
| 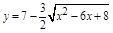
| 
| 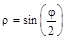
| |

| 
| 
| 
| 
| 
| |

| 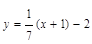
| 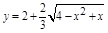
| 
| 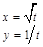
| 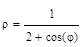
| |
| 
| 
| 
| 
| 
|
Продолжение табл. 1
 № п/п № п/п
| |||||||
 
| 
| 
| 
| 
| 
| ||
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 
| 
| ||
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 
| 
| ||

| 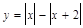
| 
| 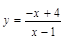
|  
| 
| ||
Продолжение табл. 1
 № п/п № п/п
| ||||||

| 
| 
| 
| 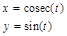
| 
| |
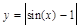
| 
| 
| 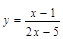
| 
| 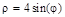
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 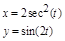
| 
|
Окончание табл. 1
 № п/п № п/п
| ||||||

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
|
Лабораторная работа № 2
Программирование ветвящихся
вычислительных процессов
Цель работы. Получить навыки программирования ветвящихся вычислительных процессов. Изучить условные операторы, переменные логического типа, логические отношения и операции.
Постановка задачи
Пусть на плоскости x, y задана область D. Требуется определить, «попадает» ли точка с координатами (x, y) в область D или нет. Если попадает, то необходимо вычислить функцию  и переменной M, значение которой является признаком «попадания» или «непопадания», присвоить значение M = 1. В противном случае вычислить
и переменной M, значение которой является признаком «попадания» или «непопадания», присвоить значение M = 1. В противном случае вычислить  и положить M = 2.
и положить M = 2.
В каждом варианте задания область D можно разбить на две подобласти: D 1, D 2. Подобласть D 1 ограничена прямыми линиями, уравнения которых нужно составить. При этом удобно использовать уравнение прямой в отрезках на осях:  . Подобласть D 2 ограничена кривой второго порядка, уравнение которой указано в задании. Варианты заданий приведены в таблице 2.
. Подобласть D 2 ограничена кривой второго порядка, уравнение которой указано в задании. Варианты заданий приведены в таблице 2.
Пояснение задачи
1. Для заданного варианта из таблицы нарисовать область D и выписать функции 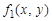 и
и  . Записать уравнения, определяющие границы области, и подготовить исходные данные (координаты точек) так, чтобы часть точек находилась внутри области D, а часть – вне ее (рис. 1). При этом для каждой четверти координатной плоскости рекомендуется выбрать по две точки.
. Записать уравнения, определяющие границы области, и подготовить исходные данные (координаты точек) так, чтобы часть точек находилась внутри области D, а часть – вне ее (рис. 1). При этом для каждой четверти координатной плоскости рекомендуется выбрать по две точки.
2. Создать на компьютере проект для решения поставленной задачи, составить и отладить программу.
3. Для выбранных точек получить и записать результаты счета.

Рис. 1. Область на плоскости x, y
Рассмотрим один из вариантов решения задачи. Пусть область D имеет вид, показанный на рис. 1, а функции  и
и 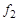 заданы как
заданы как
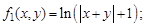
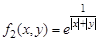 .
.
Прямой  разобьем область D на две подобласти: D 1 и D 2. Уравнения прямых, ограничивающих подобласть D 1, будут: во второй четверти
разобьем область D на две подобласти: D 1 и D 2. Уравнения прямых, ограничивающих подобласть D 1, будут: во второй четверти  ; в третьей
; в третьей  .
.
Уравнение окружности с центром в начале координат, ограничивающей подобласть D 2 при  и
и  , имеет вид
, имеет вид 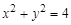 .
.
Теперь можно записать, что некоторая точка (x, y) «попадает» в область D, если она «попадает» в область D 1 или D 2, т.е. если  , и
, и  , и
, и 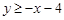 или
или  и
и  , и
, и  .
.
Точка (x, y) «не попадает» в область D, если
 и
и  , или
, или  и
и  , или
, или
 и
и  , или
, или  и
и  .
.
При выполнении задания можно проводить анализ как «попадания», так и «непопадания» точки в область D.
При составлении программы на Фортране для анализа «попадания» или «непопадания» точки в область D можно составить только одно логическое выражение с использованием следующих логических отношений и операций:
| отношения: | операции: |
| (в свободном и фиксированном форматах) < –.LT. – меньше, <= –.LE. – меньше или равно, > –.GT. – больше, >= –.GE. – больше или равно, == –.EQ. – равно, /= –.NE. – не равно. | (в порядке убывания приоритета) .NOT. – отрицание, .AND. – конъюнкция («и»), .OR. – дизъюнкция («или»), .EQV. – эквивалентность, .NEQV. – неэквивалентность. |
Результатом вычисления отношений является одно из двух логических значений.TRUE. – истина или.FALSE. – ложь. С помощью логических операций можно создавать сложные логические выражения, которые также могут принимать только два значения.TRUE. или.FALSE.
Например, точка (x, y) «попадает» в область D (рис. 1), если логическое выражение
X<=0..AND.Y<=X+4..AND.Y>=-X-4..OR.X>0..AND.Y>=0..AND.X**2+Y**2<=4.
принимает значение.TRUE. – истина.
Ветвящиеся вычислительные процессы в Фортране можно запрограммировать с помощью следующих условных операторов IF.
Логический оператор IF имеет вид
IF(L) S
Здесь L – логическое выражение, S – исполняемый оператор.
Если логическое выражение L истинно, то выполняется оператор S; если оно ложно, то выполнится следующий за IF оператор, а S не выполняется.
Блочный оператор IF имеет вид
IF(L) THEN
< блок операторов 1 >
ELSE
< блок операторов 2 >
END IF
Правило выполнения: если логическое выражение L истинно, то выполняется < блок операторов 1 >, а если оно ложно, то выполняется < блок операторов 2 >. При отсутствии альтернативы < блок операторов 2> вместе с ELSE опускается.
При необходимости дополнительных условий используется общий вид блочного оператора IF:
IF(L) THEN
< блок операторов 1 >
ELSE IF(L+) THEN
< дополнительный блок операторов >
ELSE
< блок операторов 2 >
END IF
Здесь L и L+ – основное и дополнительное логические выражения.
Правило выполнения: если логическое выражение L истинно, то выполняется < блок операторов 1 >; если выражение L ложно, а L+ истинно, то выполняется < дополнительный блок операторов >; если выражение L ложно и L+ ложно, то выполняется < блок операторов 2 >. Дополнительных условий, соответствующих им логических выражений и блоков операторов может быть несколько.
Приведем пример Фортран-программы, в которой для анализа «попадания» или «непопадания» точки используется логическая переменная C. Этой переменной присваивается значение логического выражения. Если C=.TRUE., то в блочном операторе IF (C) THEN выполняется первый блок операторов, а если C=.FALSE., то второй блок (стоящий после ELSE).
PROGRAM LAB2
LOGICAL C
REAL X, Y, Z
INTEGER I, M
OPEN(1, FILE=’LAB2.TXT’)
DO I=1,8
PRINT *, ' X=?, Y=? '; READ *, X,Y
C=X<=0..AND.Y<=X+4..AND.Y>=-X-4..OR.&
&X>0..AND.Y>=0..AND.X**2+Y**2<=4.
IF(C) THEN
PRINT *, ' YES '
Z=F1(X,Y); M=1
ELSE
PRINT *, ' NO '
Z=F2(X,Y); M=2
END IF
PRINT 2, X,Y,Z,C,