Вектор скорости направлен по касательной к траектории.

ЛИСТ 1 9 КЛАСС

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ

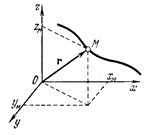
Механическим движением называется изменение положения тела относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчета. С телом отсчета связывается система координат. Совокупность тела отсчета, часов и системы координат называют системой отсчета.

Положение материальной точки М в декартовой системе координат определяется тремя координатами X_M,Y_M,Z_M. Иначе положение точки может быть задано радиус-вектором , проведенным из начала отсчета координат О до точки М.

Уравнение зависимости радиус-вектора движущейся точки от времени

или эквивалентная ему система уравнений x=x(t), y=y(t), z=z(t) называются уравнениями движения точки.

При движении точки положение её радиус-вектора в пространстве изменяется. Разность радиус-векторов, характеризующих конечное (2) и начальное (1) положения точки, движущейся в течение промежутка времени , называется вектором перемещения

(перемещением) .

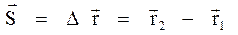
Проекции вектора перемещения на координатные оси ОX, ОY и ОZ могут быть выражены через разности координат его конца и начала:

Перемещения складываются геометрически.

Путь (S или DS) является скалярной величиной, равной длине участка траектории, пройденного движущейся точкой за данный промежуток времени. Пути, пройденные точкой за последовательные промежутки времени, складываются арифметически.

Средней скоростью за промежуток времени называется физическая величина, равная отношению вектора перемещения точки к длительности промежутка времени :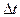

Направление вектора средней скорости совпадает с направлением вектора перемещения.

Проекция средней скорости равна коэффициенту наклона секущей к графику движения.

Скоростью (мгновенной скоростью, скоростью в данный момент времени) называется физическая величина, равная пределу, к которому стремится отношение перемещения к промежутку времени, в течение которого оно произошло при бесконечном уменьшении промежутка времени.

Вектор скорости направлен по касательной к траектории.

Проекция мгновенной скорости равна коэффициенту наклона касательной к графику движения.

Средней скалярной (средней путевой) скоростью называется физическая величина, равная отношению пути DS, пройденного точкой за промежуток времени Dt, к длительности этого промежутка.

Вопросы к зачёту:

Векторные величины. Проекция вектора на ось. Определение вектора по его проекциям. Действия с векторами и проекциями. Механическое движение. Система отсчёта. Траектория. Материальная точка. Радиус-вектор. Уравнение движения. Уравнение траектории. Перемещение. Путь. Поступательное и вращательное движение. Средняя скорость. Мгновенная скорость. Путевая скорость.

Определение средней, мгновенной и путевой скорости по графику движения.

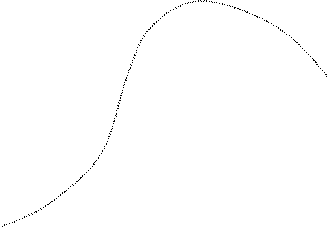
1. Точка движется по прямой. На рисунке показан график зависимости координаты точки в зависимости от времени. Найти: путь и перемещение точки за всё время движения, среднюю и среднюю путевую скорость за всё время движения, мгновенную скорость в начале и в конце движения, максимальное значение скорости.

2. Точка прошла половину пути со скоростью V₀. На оставшейся части пути она половину времени двигалась со скоростью V₁, а последний участок прошла со скоростью V₂. Найти среднюю скорость точки за всё время движения.

3. Муха сначала пролетела 10 м на север, потом 20 м на юго-восток и 5м вверх. Найти её перемещение и путь.