Свободный резерв – это наибольшее время, на которое можно задержать выполнение данной работы, не меняя раннего начала последующей. Этот резерв возможен только тогда, когда в событие входят две или более работы (зависимости), т.е. на него направлены две или более стрелки (сплошные или пунктирные). Тогда лишь у одной из этих работ раннее окончание будет совпадать с ранним началом последующей работы, для остальных же это будут разные значения. Эта разница у каждой работы и будет ее свободным резервом.
Цепь Б-К-Л-М-Р является критическим путем, значит на нем не могут быть получены полные резервы времени. Значит, корректировке могут подвергнутся пути, описываемые цепочками А-В-Д-И-Н-Р, А-В-Е-З-Н-Р, А-В-Е-З-О-С-Т, А-В-Д-И-О-С-Т, А-Г-Ж-З-О-С-Т и А-Г-Ж-З-Н-Р. Свободный резерв времени в нашем случае можем получить, рассматривая процесс выполнения работы К. Составим таблицу, наиболее полно характеризующую
временные параметры в данной сетевой модели. При этом:
· ранний срок начала работы:
 ;
;
· поздний срок начала работы:
 ;
;
· ранний срок окончания работы:
 ;
;
· поздний срок окончания работы:
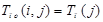 ;
;
· полный резерв:
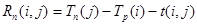 ;
;
· свободный резерв:
 .
.
Процесс заполнения таблицы 2 произведем по следующему алгоритму:
1) Графа код работы заполняется на основе сетевого графика или перечня работ, расположенных в порядке их выполнения.
2) Количество предшествующих работ для исходного события равно 0, для остальных работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
3) Третья графа заполняется на основе сетевого графика или перечня работ с временными оценками.
4) Раннее начало работ, выходящих из исходного события, равно 0, а раннее окончание работ определяется путем выбора максимального их сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ, указанному в графе 1.
Таким образом, нельзя определить раннее начало последующих работ, не найдя раннего окончания предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы.
5) Продолжительность критического пути находится после заполнения граф 4 и 5, как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию. Найденная величина критического пути заносится в графу 7 (позднего окончания работ) для всех работ, ведущих к завершающему событию.
6) Заполнение графы 7 (кроме последней ее строки) – ведется снизу вверх следующим образом. Находятся все работы, последующие за рассматриваемой работой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из полученных величин заносится в графу 7 против рассматриваемой работы.
7) Данные графы 6 (позднее начало работы) находят как разность позднего окончания этих работ и их продолжительности (графа 7 - графа 3).
8) Полный резерв времени работы (графа 8) определяется разностью между значениями в графах 7 и 5 (или 6 и 4).
9) Резерв времени события j (графа 10) определяется следующим образом. В графе 7 отыскивается позднее окончание работы, заканчивающееся событием j. В графе 4 отыскивается раннее начало работы, начинающееся событием j. Разность этих величин является искомым резервом времени события j.
10) Свободный резерв времени работы Ксi,j определяется в результате вычитания значений графы 10 из значений граф 8.
Таблица 2 – Расчёт параметров работ
| Код работы | 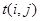
| 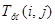
| 
| 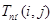
| 
| 
| 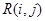
| 
|
| 1,2 | ||||||||
| 1,3 | ||||||||
| 2,4 | ||||||||
| 2,5 | ||||||||
| 3,9 | ||||||||
| 4,6 | ||||||||
| 5,6 | ||||||||
| 5,7 | ||||||||
| 6,8 | ||||||||
| 7,8 | ||||||||
| 8,11 | ||||||||
| 8,12 | ||||||||
| 9,10 | ||||||||
| 10,11 | ||||||||
| 11,14 | ||||||||
| 12,13 | ||||||||
| 13,14 |
Изобразим схематично сетевую модель расчёта (рис. 17).

Рисунок 17