Уточнение корней нелинейного уравнения методом половинного деления

Брянский колледж экономики, статистики и информатики – филиал МЭСИ

 

УТВЕРЖДАЮ:

Заместитель директора по УМР

____________Т.Н. Кузина

«____» _______________

 

 

 

ИНСТРУКЦИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №2

«Численное решение нелинейных уравнений»

По предмету «Численные методы» для студентов специальности 230105

«Программное обеспечение ВТ и автоматизированных систем»

 

 

Инструкция составлена преподавателем Ноздрачевой Н.Л.

 

Согласовано на заседании цикловой комиссии ИТ и ВТ

Протокол заседания № ___ от ____________ 200 г.

Председатель комиссии _________ С.И. Тетерина

 

Брянск

 

Содержание

 

 

1. Цель работы.

2. Приборы и оборудование.

3. Общие теоретические сведения.

4. Задание.

5. Порядок выполнения работы.

6. Отчет о выполненной работе.

7. Контрольные вопросы.

8. Литература.

1. Цель работы:

 

1.1. Закрепить знание основных алгоритмов отделения и уточнения корней нелинейных уравнений.

1.2. Найти приближенные значения корней уравнения с заданной точностью, используя различные методы.

· половинного деления;

· методом хорд;

· методом касательных;

· комбинированным методом.

1.3. Сравнить результаты, полученные различными методами.

 

2. Приборы и оборудование:

2.1. ПК, математическая система MathCad.

 

 

Общие теоретические сведения

Постановка задачи

При решении ряда задач физики, механики и техники возникает необходимость решения уравнений с одной переменной. В общем случае нелинейное уравнение можно записать в виде: f(x)=0, где функция y=f(x) определена и непрерывна на промежутке {A, B}. Корнем этого уравнения является такое число c из области определения функции, для которого справедливо равенство f(c)=0.

Поскольку подавляющее большинство нелинейных уравнений не решается путем аналитических преобразований (точными методами), на практике их решают численными методами. Решить такое уравнение численными методами значит установить, имеет ли оно корни, сколько корней, и найти все его корни с заданной точностью.

Задача численного решения уравнений состоит из двух этапов:

1. Отделение корней уравнения, т. е. нахождение достаточно малых промежутков из рассматриваемой области {A, B}, в которых содержится единственный корень.

2. Уточнение корней уравнения, т. е. нахождение корней с заданной точностью.

 

Отделение корней

Во многих случаях отделение корней можно произвести графически. Для этого необходимо построить график функции y=f(x) и найти достаточно малые отрезки, содержащие по одной точке пересечения графика с осью ОХ. Иногда построение значительно упрощается, если функцию y=f(x) представить в виде f₁(x)=f₂(x) и найти отрезки оси ОХ, содержащие координаты х точек пересечения.

Отделение корней можно также произвести с помощью соответствующей компьютерной программы.

Пусть имеется уравнение f(x)=0, причем все интересующие вычислителя корни находятся на отрезке [A, B], на котором функция определена и непрерывна. Требуется отделить корни уравнения, т.е. найти отрезки [a, b] [A, B], содержащие по одному корню. Очевидно, что если на отрезке [a, b] функция меняет знак, то на этом отрезке находится, по крайней мере, один корень уравнения f(x)=0. Если длина отрезка [a, b] очень мала и f(a)*f(b)<0, то можно считать, что на этом отрезке находится единственный корень.

Таким образом, просматривая отрезок [A, B] с некоторым достаточно малым шагом h и проверяя условие f(х)*f(x+h)<0 можно отделить все корни уравнения на отрезке [A, B]. Если получится, что на некотором шаге f(х)*f(x+h)=0 и f(х-h)*f(x)¹0, то можно считать, что x+h – точное значение корня.

Уточнение корней нелинейного уравнения методом половинного деления

Пусть на некотором отрезке [a, b] имеется единственный корень уравнения f(x)=0.

Разделим [a, b] пополам точкой . Если f(c)=0, то x=c - корень уравнения f(x)=0 на [a, b]. Наиболее вероятно, что f(c)≠0. Тогда возможны 2 случая:

1. f(a)*f(с)<0 2. f(a)*f(с)>0

 

 

Выбирая в каждом случае тот из отрезков, на котором функция меняет знак и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Данный метод позволяет находить корни уравнения с заданной точностью е. Действительно, если на каком-то этапе процесса деления получен отрезок [a', b'], содержащий корень, то приняв x≈(a'+b')/2, мы найдем корень с точностью е 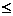(b'-a')/2.

 

 

Пусть уравнение f(x)=0 имеет единственный корень на отрезке [a, b]. Если отрезок [a, b] достаточно мал, то можно считать, что функция y=f(x) монотонна на этом отрезке и не меняет направление выпуклости. Значит на отрезке [a, b] нет точек максимума и минимума, т.е. . Т.к. направление выпуклости не меняется то и 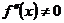. Получаем четыре вида графиков, которые объединяются в два типа.

I. тип. Условие: , где x - любая точка [a, b].     B

II. тип. Условие: , где x - любая точка [a, b].

 

Пусть x* - искомый корень уравнения f(x)=0. Заменим кривую графика на хорду АВ. Уравнение прямой, проходящей через точки А (а, f(а)) и В(b, f(b)) имеет вид: , где (x, y) – любая точка прямой АВ. В качестве этой точки возьмем точку пересечения хорды с осью ОХ, т.е.

 

(x₁, 0). Получим или

Рассмотрим случай, когда кривая графика функции y=f(x) относится к I типу. Через точки А₁ и В проводим следующую хорду. Она пересекает ось ОХ в точке х_{2 .} Аналогично получаем

,

…………………………………

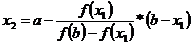(1)

 

Полученная таким образом формула называется формулой метода хорд для кривых I-го типа.

Очевидно, что последовательность значений х₁, х₂, х₃, …,х_n стремится к корню уравнения х^*, а значит этот корень можно найти с заданной точностью.

В рассмотренном выше случае для кривых I-го типа, правым концом всех проведенных хорд была точка В. Если, кривая относится ко II-му типу, то неизменным концом хорд будет точка А. Значит в формуле (1) b поменяется на а. Формула будет иметь вид:

(2)

Если на n-ом шаге , то считается, что необходимая точность е достигнута.