Брянский колледж экономики, статистики и информатики
УТВЕРЖДАЮ:
Заместитель директора по УМР
____________Т.Н. Кузина
«____» _______________
ИНСТРУКЦИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №8
«Численное решение обыкновенных дифференциальных уравнений»
По предмету «Численные методы» для студентов специальности 230105
«Программное обеспечение ВТ и автоматизированных систем»
Инструкция составлена преподавателем Ноздрачевой Н.Л.
Согласовано на заседании цикловой комиссии математики, информатики и программирования
Протокол заседания № ___ от ____________ 200 г.
Председатель комиссии _________ Н.К. Минина
Брянск
Содержание
1. Цель работы.
2. Приборы и оборудование.
3. Общие теоретические сведения.
4. Задание.
5. Порядок выполнения работы.
6. Отчет о выполненной работе.
7. Контрольные вопросы.
8. Литература.
1. Цель работы:
1.1. Закрепить знание основных алгоритмов решения обыкновенных дифференциальных уравнений.
1.2. Разработать программу решения обыкновенных дифференциальных уравнений методами:
- методом Эйлера;
- методом Эйлера с двойным счетом;
- методом Эйлера – Коши с двойным счетом;
- методом Рунге – Кутта.
1.3. Найти решения обыкновенных дифференциальных уравнений различными методами.
1.4. Сравнить результаты, полученные различными методами.
1.5. Закрепить умения и навыки работы с программой и основными компонентами в среде программирования Delphi.
2. Приборы и оборудование:
2.1. ПК, система программирования Delphi.
Общие теоретические сведения
Постановка задачи
Обыкновенным дифференциальным уравнением называется уравнение вида  Решить такое уравнение численным методом это значит для заданной последовательности аргументов
Решить такое уравнение численным методом это значит для заданной последовательности аргументов  и числа
и числа  , не определяя функции
, не определяя функции  найти такие значения
найти такие значения  что
что  где
где  и
и 
|
|
Таким образом, численные методы позволяют вместо нахождения функции  получить таблицу значений этой функции для заданной последовательности аргумента и начального условия
получить таблицу значений этой функции для заданной последовательности аргумента и начального условия 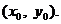
Метод Эйлера
Пусть дано дифференциальное уравнение  с начальным условием
с начальным условием  Требуется найти решения данного уравнения на
Требуется найти решения данного уравнения на 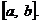
Разобьём отрезок  на n равных частей. Получили последовательность чисел
на n равных частей. Получили последовательность чисел  . Шаг
. Шаг 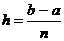 или
или  . Проинтегрируем данное дифференциальное уравнение по
. Проинтегрируем данное дифференциальное уравнение по  . Получим:
. Получим: 
|
 достаточно малы, то подынтегральную функцию
достаточно малы, то подынтегральную функцию  можно принять постоянной.Значит:
можно принять постоянной.Значит:  .
.
Отсюда получаем формулу Эйлера:
Таким образом, если известна функция  , начальное условие
, начальное условие 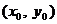 , шаг h и отрезок
, шаг h и отрезок  , то по этой формуле можно найти все решения дифференциального уравнения
, то по этой формуле можно найти все решения дифференциального уравнения  на данном отрезке.
на данном отрезке.
Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага возрастает. Поэтому он применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу этого метода, являются исходными для ниже следующих методов.
Метод Эйлера – Коши (уточненный метод Эйлера)
|
 по формуле:
по формуле:
|
 по формуле с использованием ранее найденного значения
по формуле с использованием ранее найденного значения  :
:|
|
3.4. Метод Рунге – Кутта
Это один из методов повышенной точности.
 |