ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА

КОМПЛЕКСНЫЕ ЧИСЛА

 

Решение многих задач сводится к решению алгебраических уравнений.

Рациональные и иррациональные числа образуют множество действительных чисел. Однако, действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение

х² + 1 = 0

не имеет действительных корней. Поэтому приходится расширять множество действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида х² + а² = 0 имели решения.

Корень уравнения х² + 1 = 0 или х² = -1 называется мнимой единицей и обозначается буквой i. Таким образом, символ i удовлетворяет условию

i² = -1

Комплексным числом называется выражение вида a + bi, где a и b - действительные числа, i - мнимая единица. Число a называется действительной частью комплексного числа, а число bi - мнимой частью. Комплексное число обозначается буквой z. Запись комплексного числа в виде

z = a + bi

называется алгебраической формой записи комплексного числа.

Комплексное число z = 0+bi называется чисто мнимым, z = 0+bi = bi. При решении задач учитывать z = a+0i = a. Комплексное число z = 0+0i называется нулем. Комплексные числа a+bi и a-bi называются сопряженными.

 

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ

Суммой двух комплексных чисел z₁ = a₁ + b₁i и z₂ = a₂ + b₂ i

называется комплексное число

z₁ + z₂ = (a₁+ a₂) + (b₁ + b₂) i

 

Произведением двух комплексных чиселz₁ = a₁ + b₁i и z₂ = a₂ + b₂iназывается комплексное число

z₁ z₂ = (a₁a₂-b₁b₂ ) + (a₁b₂+a₂b₁) i

Вычитание комплексных чисел вводится как операция, обратнаясложению.

Деление - как операция, обратная умножению.

Формулы не нуждаются в запоминании. Формулы суммы, разности, произведения комплексных чисел получаются автоматически, если выполнять соответствующие действия и заменить i² = -1.

При делении на комплексное число достаточно умножить числитель и знаменатель дроби на число, сопряженное знаменателю.

 

ПРАКТИЧЕСКИЕ ЗАДАНИЯ

1. Найти сумму комплексных чисел z₁ = 2+(- 1)i и z₂ = (-1) + 3i

 

2. Найти разность комплексных чисел z₁ = 4 + 5i и z₂ = -2 + 3i

 

3. Найти произведение комплексных чисел z₁ = 2 - 3i и

z₂ = -4 + 2i

 

4. Вычислить (5 + 10i) + (1 + 2i) (3 - 4i)

5. Выполнить действие а)

 

б)

 

 

в)

 

6. Вычислить число z , обратное числу z = 3 - i

 

7. Вычислить степени i³, i⁴, i⁵, i^-1, i^-2, i^-3

 

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ

КОМПЛЕКСНОГО ЧИСЛА

 

Комплексное число z = a + bi изображается на координатной плоскости точкой М(a;b) или вектором ОМ, начало которого совпадает с началом координат, а конец - с точкой М.

 

B b 0

Координатная плоскость называется комплексной плоскостью, ось абсцисс (Ох) -

y

действительной осью, ось ординат (Оу) -

мнимой осью.

 

j a A x

М(a;b)

Модулем комплексного числа называется абсолютная величина вектора, соответствующего этому числу.

Для модуля числа z = a + bi используются обозначения r, |z| или |a + bi|. На основании теоремы Пифагора

 

|z| = r =

Аргументом комплексного числа называется величина угла j между положительным направлением действительной оси и вектором, соответствующим этому числу

j = arctg ½ ½

(arctg½ ½ читается: угол, тангенс которого равен ).

Обозначения для аргумента числа z = a + bi: j, arg z или

arg (a + bi).

 

 

ПРАКТИЧЕСКИЕ ЗАДАНИЯ

1. Построить радиус-векторы, соответствующие комплексным числам:

а) z = 2; б) z = -3; с) z = -3i; d) z = -2i; е) z = 2 + 3i.

y

 

2. Найти модуль и главное значение аргумента комплексных чисел:

а) z = 1 + i; б) z = i;

ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА

 

Из рис.1, из треугольника ОМА можно выразить действительные числа a и b через модуль r и аргумент j числа z следующим образом:

a = r cos j

b = r sin j,

таким образом, комплексное число z можно записать в виде:

 

z = r (cos j + i sin j),

где r - модуль комплексного числа;

j- один из его аргументов.

Запись в таком виде называется тригонометрической формой записи комплексного числа.

Для того, чтобы перейти от алгебраической формы записи комплексного числа z = a + bi к тригонометрической, достаточно найти его модуль и один из аргументов. Аргумент комплексного числа z = a + bi можно находить из системы

cos j =

sin j =

 

ПРИМЕРЫ: 1. Записать число z = - - i в тригонометрической форме

Из условия a = - ; b = -1. Следовательно,

r = = = 2.

Аргумент заданного комплексного числа

j=arctg| 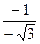|=arctg =arctg .

 

y

 

^{- O}

-1 x

 

 

Вектор, соответствующий данному комплексному числу лежит в III координатной четверти. Поэтому j=7p/6 (см. таблицу значений тригонометрических функций некоторых углов). Зная r и j перейдем к тригонометрической записи заданного комплексного числа.

z= - - i = 2 (cos 7p/6 + i sin 7p/6).

 

2. Записать число z = 2(cos 330 ° + i sin 330 ° ) в алгебраической форме.

Найдем cos 330°, sin 330°.

cos 330° = cos (360° ^- 30°) = cos 30°= ;

sin 330°= cos (360°- 30°) = -sin 30 = - .

Тогда a = 2() = ,

b = 2(- ) = -1.

Следовательно, z = 2(cos 330° + i sin 330°) = - i.