Лабораторная работа № 3
АНАЛИЗ ВРЕМЕННЫХ РЯДОВ, ТРЕНД РЯДА ДИНАМИКИ, ТОЧЕЧНАЯ ОЦЕНКА ПРОГНОЗА
Цель работы: научиться выполнять прогнозирование временного ряда данных с помощью средств Microsoft Excel (или других программных средств) и математически.
Содержание работы:
1. Анализ временных рядов.
2. Прогноз, характеристики и параметры прогнозирования.
3. Линейная, нелинейная, многомерная регрессия.
4. Уравнение тренда временного ряда.
Порядок выполнения работы:
1. Изучить методические указания.
2. Выполнить задания с использованием средств MS Excel.
3. Оформить отчет, сделав выводы по заданиям.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
1. Временно́й ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов: - периода времени, за который или по состоянию на который приводятся числовые значения; - числовых значений того или иного показателя, называемых уровнями ряда. Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичными примерами временных рядов можно назвать изменение температуры объекта, пропускной способности сети, интенсивности абонентов в сети, при анализе которых пытаются определить основное направление развития (тенденцию или тренд).
|
|
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
2. Прогноз (от греч. πρόγνωσις – предвидение, предсказание) – предсказание будущего с помощью научных методов, а также сам результат предсказания.
Прогноз – это научная модель будущего события, явлений и т.п. Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса. Прогнозы делятся: - по срокам: краткосрочные, среднесрочные, долгосрочные; - по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, страновые, мировые (глобальные). К основным методам прогнозирования относятся: - статистические методы; - экспертные оценки (метод Дельфи); - моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний.
Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
|
|
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования, которые представляют собой совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов. Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз. Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования. Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории, ретроспективным периодом.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
|
|
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений. Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах. Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия.
Одним из методов, используемых для прогнозирования, является регрессионный анализ. Регрессия – это статистический метод, который позволяет найти уравнение, наилучшим образом описывающее совокупность данных, заданных таблицей.
| X | X1 | X2 | …. | Xi | … | Xn |
| Y | Y1 | Y2 … | … | Yi | … | Yn |
На графике данные отображаются точками. Регрессия позволяет подобрать к этим точкам кривую у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к табличным данным.
По полученному уравнению можно вычислить (сделать прогноз) значение функции у для любого значения х, как внутри интервала изменения х из таблицы (интерполяция), так и вне его (экстраполяция).
3. Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз). Значения временного ряда можно представить в виде: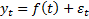 
, где f(t) – неслучайная функция, описывающая связь оценки математического ожидания со временем, 
– случайная величина, характеризующая отклонение уровня от f(t). Неслучайная функция f(t) называется трендом. Тренд отражает характерное изменение (тенденцию) 
за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами (t,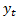 
) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие. Уравнение тренда линейного вида будем искать в виде 
, где
.
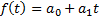MS Excel позволяет наглядно отображать тенденцию данных с помощью линии тренда, которая представляет собой интерполяционную кривую, описывающую отложенные на диаграмме данные. Для того, чтобы дополнить диаграмму исходных данных линией тренда, необходимо выполнить следующие действия:
· выделить на диаграмме ряд данных, для которого требуется построить линию тренда;
· в меню Диаграмма выбрать команду Добавить линию тренда;
· в открывшемся окне задать метод интерполяции (линейный, полиномиальный, логарифмический и т. д.), а также через команду Параметры – другие параметры (например, вывод уравнения кривой тренда, коэффициента детерминированности r2, направление и количество периодов для экстраполяции (прогноза) и др.);
· нажать кнопку ОК. Чтобы отобразить на графике (гистограмме и др.) новые, прогнозируемые в результате регрессионного анализа данные, нужно:
· определить их с помощью функции ТЕНДЕНЦИЯ, ПРЕДСКАЗ или другим способом,
· выделить на диаграмме нужную кривую, щелкнув по ней мышью,
· в меню Диаграмма выбрать команду Добавить данные…, в появившемся окне выбрать диапазон ячеек с новыми данными вручную или протащив по ним курсор при нажатой левой клавише мыши, нажать ОК.
На диаграмме появится продолжение кривой, построенной по новым данным.
Задание. Временной ряд приведен в таблице. Используя средства MS Excel:
1) построить график временного ряда;
2) добавить линию тренда и ее уравнение;
3) найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
4) построить график временного ряда и полученной функции тренда в одной системе координат;
5) определить параметры уравнения тренда с помощью функции Excel
6) Провести анализ качества модели с использованием MAD и MAPE.
7) Сделать выводы
Варианты.
1. Имеются данные об изменении пропускной способности сети (байт/с) в зависимости от числа абонентов, полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
| |||||||
|
2. Имеются данные об изменении пропускной способности сети (байт/с) и загрузки сети конфликтами (байт), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| |||||||
|
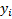
| 0,000000091 | 0,000000205 | 0,000000369 | 0,000000136 | 0,000000132 | 0,000000540 | 0,000001202 |
3. Имеются данные о динамике загрузки сети конфликтами (байт) и времени восстановления сети после конфликта (с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| 0,000000091 | 0,000000205 | 0,000000369 | 0,000000136 | 0,000000132 | 0,000000540 | 0,000001202 |
|
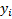
| 0,00002 | 0,000023 | 0,000025 | 0,000021 | 0,00002 | 0,000025 | 0,00003 |
4. Имеются данные о динамике загрузки сети конфликтами (байт) и интенсивности абонентов (байт/с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице
| t | |||||||
|
| 0,000000091 | 0,000000205 | 0,000000369 | 0,000000136 | 0,000000132 | 0,000000540 | 0,000001202 |
|
|
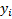
5. Имеются данные об изменении пропускной способности сети (байт/с) и интенсивности абонентов (байт/с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| |||||||
|
|
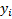
6. Имеются данные об изменении пропускной способности сети (байт/с) и времени восстановления сети после конфликта (с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| |||||||
|
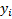
| 0,00002 | 0,000023 | 0,000025 | 0,000021 | 0,00002 | 0,000025 | 0,00003 |
7. Имеются данные о динамике интенсивности абонентов (байт/с) и загрузке сети данными (байт), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| |||||||
|
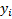
| 0,028564 | 0,035872 | 0,038562 | 0,032558 | 0,031757 | 0,042418 | 0,048591 |
8. Имеются данные о динамике интенсивности абонентов (байт/с) и времени восстановления сети после конфликта (с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| |||||||
|
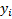
| 0,00002 | 0,000023 | 0,000025 | 0,000021 | 0,00002 | 0,000025 | 0,00003 |
9. Имеются данные о динамике загрузки сети данными (байт) и времени восстановления сети после конфликта (с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| 0,028564 | 0,035872 | 0,038562 | 0,032558 | 0,031757 | 0,042418 | 0,048591 |
|
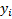
| 0,00002 | 0,000023 | 0,000025 | 0,000021 | 0,00002 | 0,000025 | 0,00003 |
10. Имеются данные о динамике загрузки сети данными (байт) и пропускной способности сети (байт/с), полученные при замерах через каждые полчаса. Эти данные приведены в таблице:
| t | |||||||
|
| 0,028564 | 0,035872 | 0,038562 | 0,032558 | 0,031757 | 0,042418 | 0,048591 |
|
|
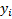