Средние показатели вариации

Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учёта знака этих отклонений

Дисперсия s² (средний квадрат отклонений) определяется по формуле:

Чем меньше дисперсия, тем лучше средняя арифметическая отражает собой всю представленную совокупность.

Среднее квадратическое отклонение s может быть найдено таким образом:

Дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить степень колебания данных вокруг среднего значения.

Интерпретация понятий

Дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить разброс данных вокруг среднего значения, т.е. сколько элементов выборки меньше среднего, а сколько – больше. Дисперсия обладает ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения (квадратный %, квадратный доллар и т.д.). Поэтому естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерения - %, доллары …

Стандартное отклонение позволяет оценить величину колебания значений вокруг среднего значения. Практически во всех ситуациях наблюдаемые величины лежат в интервале плюс-минус одно стандартное отклонение от среднего значения. Поэтому, зная среднее арифметическое и среднее квадратическое (стандартное) отклонение можно определить интервал, которому принадлежит основная масса данных.

Суммируем вышесказанное

ü Чем больший разброс имеют данные, тем больше их размах, межквартильный размах, дисперсия и стандартное отклонение

ü Чем более сконцентрированы данные, или однородны, тем меньше их размах, межквартильный размах, дисперсия и стандартное отклонение

ü Если все элементы выборки равны между собой (т.е. разброс отсутствует), межквартильный размах, дисперсия и стандартное отклонение равны нулю.

ü Ни одна из оценок изменчивости данных (размах, межквартильный размах, дисперсия и стандартное отклонение) не может быть отрицательной.

18. Показатели относительного рассеивания.

Коэффициент осцилляции К₀ отражает относительные колебания крайних значений признака вокруг средней:

Относительное линейное отклонение K_d характеризует долю усреднённого значения абсолютных отклонений от средней величины.

Коэффициент вариации u определяют по формуле:

Коэффициент вариации измеряет рассеивание данных относительно среднего значения. Измеряется в %, а не в единицах измерения исходных данных.

Коэффициент вариации позволяет сравнить две выборки, элементы которых выражаются в разных единицах измерения.

Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние (серединные) характеристики достаточно надежно характеризуют совокупность по варьирующему признаку, когда относительные показатели вариации больше 35% - то ненадежно. В этом случае варианты ряда распределения существенно отличаются от средних характеристик.

19. Виды дисперсии.

Виды дисперсии – это показатель изменения признака в совокупности.

Определим три вида дисперсии:

общую дисперсию ,

межгрупповую дисперсию ,

среднюю внутригрупповых дисперсий .

Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности.

где - общая средняя для всей изучаемой совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака фактора, положенного в основу группировки.

где - средняя по отдельным группам;

- средняя общая;

- численность отдельных групп.

Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Это вариация результативного признака, которая возникает под влиянием всех остальных факторов, кроме группировочного.

где - дисперсия в каждой группе.

Большую практическую значимость имеет правило сложения дисперсий:

Коэффициент детерминации h² находят по формуле: .

Он характеризует долю вариации группировочного признака в общем объеме вариации или на сколько процентов уровень результативного признака определяется группировочным признаком.

Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением.

Это отношение характеризует тесноту связи между признаками, т.е. близость корреляционной (неполной) зависимости к функциональной (полной). Этот показатель изменяется от нуля до единицы. Точность его зависит от размеров совокупности: чем больше совокупность, тем он надежнее. Недостатки эмпирического корреляционного отношения: невозможность определить направление связи (прямая зависимость или обратная); невозможность определения формы связи.

20. Анализ данных с помощью блочных диаграмм. Базовые показатели.

Стандартная ошибка – стандартное отклонение деленное на квадратный корень объема выборки.

Ассиметричность характеризует отклонение от симметричности распределения и является функцией, зависящей от куба разностей между элементами выборки и средним значением.

Эксцесс – это мера относительной концентрации данных вокруг среднего значения по сравнению с хвостами распределения; зависит от разностей между элементами выборки и средним значением, возведенными в четвертую степень.

Основные характеристики позволяют описать свойства данных и перейти к более глубоким исследованиям. Довольно часто для анализа данных применяется подход, основанный на пятерке базовых показателей и построении блочной диаграммы.

Блочная диаграмма представляет собой удобное средство для изображения пяти базовых показателей:

21. Дисперсия альтернативного (качественного признака).

Альтернативные – это признаки, которыми обладают одни единицы совокупности и не обладают другие.

Наличие изучаемого признака обозначается 1, а его отсутствие 0.

Доля показателей, обладающих изучаемым признаком, обозначается – р, а доля значений, не обладающих признаком, обозначается q.

P + q = 1

Найдем их средние значения и дисперсию.

22. Основная задача выборочного обследования.

Статистика не всегда имеет дело с данными сплошного наблюдения. Из всех видов несплошного наблюдения главным является выборочное наблюдение, т.к. только выборка позволяет распространить данные, полученные по части совокупности, на всю совокупность.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности (генеральной совокупности) устанавливаются по некоторой её части (выборочной совокупности или просто выборке) на основе положений случайного отбора.

В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка производится с уничтожением или разложением на составные части обследуемых образцов.

Причины использования выборочного метода:

1) повышение точности данных

2) экономия материальных, трудовых, финансовых ресурсов и времени

3) без выборки не обойтись, когда наблюдение связано с порчей наблюдаемых объектов)

Далее будем использовать следующие понятия:

Генеральная совокупность – это подлежащая изучению статистическая совокупность, из которой производится отбор части единиц

Выборочная совокупность (выборка) – отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию.

Суть выборочного метода:

получение характеристик изучаемой совокупности (генеральной) по обследованию некоторой ее части (выборке).

Выборочный метод использует два основных вида обобщающих показателей:

- относительную величину альтернативного (качественного) признака;

Она характеризует долю (удельный вес) единиц в статистической совокупности, которые отличаются от других единиц только наличием изучаемого признака.

- среднюю величину количественного признака.

Это обобщающая характеристика варьирующего признака, который имеет различные значения у отдельных единиц статистической совокупности

Определим следующие величины для генеральной совокупности:

- доля единиц с изучаемым признаком (генеральная доля) Р;

- средняя величина варьирующего признака (генеральная средняя)

для выборки:

- доля изучаемого признака (выборочная доля или частота) w;

- средняя величина в выборке (выборочная средняя).

Тогда основная задача выборочного обследования состоит в том, чтобы на основе характеристик w и из выборки получить достоверные суждения о Р и в генеральной совокупности.

Их расхождения измеряются средней ошибкой выборки m.

23. Ошибка выборки.

Ошибка выборки – это объективно возникающие расхождения между характеристиками выборки и генеральной совокупности

В математической статистике доказывается, что среднее значение ошибки выборки определяется по формуле:

где - генеральная дисперсия; n – объем выборки.

Однако обычно неизвестно, наоборот, его как правило надо определить.

Поэтому используют соотношение

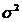, где - дисперсия в выборочной совокупности.

Если n – велико, то стремится к 1.

Тогда 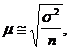(1)

где s²- дисперсия в выборочной совокупности; n - объём выборки.

Формула (1) используется при повторном отборе.

При этом для показателя доли альтернативного признака w дисперсия в выборочной совокупности определяется по формуле:

, где w=m/n

m – доля единиц с изучаемым признаком; n – объем выборки.

Для бесповторного отбора: (2)

где N - численность генеральной совокупности.

Повторный отбор – каждая попавшая в выборку единица после фиксации значения изучаемого признака, должна быть возвращена в генеральную совокупность, где ей опять предоставляется равная возможность попасть в выборку.

Возможные значения, в пределах которых может находиться доля единиц, обладающих изучаемым признаком, в генеральной совокупности определяется по формуле: . (3)

Для средних значений в генеральной совокупности установлены следующие границы: (4)

Формулы (3) и (4) гарантированы не с абсолютной достоверностью, а лишь с определённой степенью вероятности.

В математической статистике доказывается, что пределы значений характеристик генеральной совокупности (Р и ) отличаются от характеристик выборочной совокупности (w и ) на величину лишь с определенной вероятностью = 0,683. Т.е. в 317 случаях из 1000 значения могут выйти из этих пределов.

Эту вероятность можно увеличить, увеличив в t раз среднюю ошибку m.

Здесь t - коэффициент доверия.

При t = 2 доверительная вероятность = 0,954

При t = 3 доверительная вероятность = 0,997 (т.е. выход в 3-х случаях из 1000)

Величина коэффициента доверия t зависит о доверительной вероятности и определяется по специальным таблицам, исчисленным применительно к случаю нормально распределенной совокупности (таблицы интегральной функции Лапласа).

Тогда:

При изучении доли альтернативного признака показатели соотносятся следующим образом: , (5)

При изучении средней величины: . (6)

Ошибки репрезентативности выборочного наблюдения это разновидность случайных ошибок. Они появляются как результат неполноты наблюдения. Если провести несколько выборочных наблюдений по одной совокупности, то полученные расхождения между показателями выборочной и генеральной совокупностей (т.е. ошибки выборки) будут различны как по знаку, так и по величине. Вот почему с помощью теорем математической статистики определяется средняя из возможных ошибок.

Смысл средней ошибки выборки: средняя ошибка выборки, по существу, это средняя квадратическая величина из отдельных ошибок, взвешенная по вероятности их возникновения.

Предельная ошибка выборки D находится следующим образом:

D = t · m. (7)

t - зависит от вероятности, с которой гарантируется величина предельной ошибки выборки.

Расчёт D при бесповторном отборе может быть записан следующими алгоритмами:

- доля альтернативного признака (8)

- средняя величина количественного признака (9)

Если процент единиц, взятых в выборку небольшой (до 5 %) то 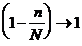и расчёт производится по формулам повторного отбора:

, (10)

. (11)

Однако в этом случае мы несколько преувеличиваем результаты выборки (т.е. немного повышается средняя ошибка выборки).

24. Определение оптимальной численности выборки.

Размер ошибки выборки прежде всего зависит от численности выборочной совокупности n. При доведении N до n ошибка выборки m =0. Однако это требует увеличения объемов исследований, дополнительных затрат труда и материальных средств.

Определение оптимальной численности выборки основывается на формуле предельной ошибки выборки. Необходимая численность выборки n_х (для среднего значения) и n_w (для доли альтернативного признака) определяется как:

отсюда (12)

отсюда (13)

В случае бесповторного отбора величины (12) и (13) примут следующий вид:

(14)

(15)

25. Малая выборка.

Под малой выборкой (МВ) понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности.

К минимальному объему выборки прибегают, когда большая выборка невозможна, или экономически невыгодна (если проведение исследования связано с порчей или уничтожением обследуемых образцов).

Объем малой выборки обычно не превышает 30 единиц, но м.б. до 4-5 единиц.

Первые работы в области теории малой выборки были выполнены английским статистиком В. Госсетом в 1908г. (псевдоним Стьюдент) и продолжены в исследованиях Р. Фишера.

Величина ошибки МВ определяется по формулам, отличным от формул выборочного наблюдения со сравнительно большим объемом выборки (n > 100). Средняя ошибка малой выборки исчисляется по формуле:

где - дисперсия малой выборки. (16)

При МВ величина имеет существенной значение, поэтому вычисление дисперсии малой выборки проводится с учетом числа степеней свободы.

Число степеней свободы – это количество вариантов, которые могут принимать произвольные значения, не меняя величины средней.

При определении дисперсии число степеней свободы = n – 1,

Тогда дисперсия МВ находится по формуле: (17)

Предельная ошибка малой выборки: D_мв = t · m_мв.

При этом для МВ t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n.

Для отдельных значений t и n доверительная вероятность МВ определяется по таблицам Стьюдента, в которых даны распределения стандартизованных отклонений:

(18)

При увеличении n распределение Стьюдента приближается к нормальному и при

n = 20 оно уже мало отличается от нормального распределения.

26. Распространение характеристик выборки на генеральную совокупность.

В зависимости от цели исследования применяются следующих два метода:

1) способ прямого пересчета показателей выборки для генеральной совокупности

2) посредством расчета поправочных коэффициентов.

1) При использовании способа прямого пересчета показатели выборочной доли или средней распространяются на генеральную совокупность с учетом ошибки выборки.

2) способ поправочных коэффициентов применяется, если целью выборочного метода является уточнение результатов сплошного учета:

Распространение выборочных данных на генеральную совокупность производится с учетом доверительных интервалов. Для этого соответствующие обобщающие показатели выборочной совокупности w и корректируются величиной предельной ошибки выборки ∆_w и :

Для доли альтернативного признака:

Для средней величины количественного признака:

27. Способы отбора единиц из генеральной совокупности.

Практика применения выборочного метода использует следующие методы отбора единиц из генеральной совокупности:

Индивидуальный отбор – в выборку отбираются отдельные единицы.
Групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц.
Комбинированный отбор – сочетание индивидуального и группового отбора.

Методы отбора определяются способами формирования выборочной совокупности:

а) собственно-случайная выборка

б) механическая выборка

в) типическая выборка

г) серийная выборка

д) моментная выборка

е) комбинированная выборка

Собственно-случайная выборка – случайный (непреднамеренный) отбор отдельных единиц из генеральной совокупности. Количество отобранных единиц определяется исходя из принятой доли выборки К_в.

К_в= n/N.

Принцип случайности попадания в выборку устраняет возникновение систематических (тенденциозных) ошибок выборки и обеспечивает ее репрезентативность (представительность).

Формирование этой выборки производится с помощью специальных фишек; таблицы случайных чисел.

Эта выборка м.б. осуществлена по схемам повторного и бесповторного отбора.

Для вычисления средней ошибки выборки используются формулы:

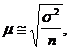
(19)

Механическая выборка – генеральная совокупность разбивается на равные интервалы (группы). Размер интервала в генеральной совокупности равен обратной величине доли выборки.

Из каждой группы в интервал выбирается одна единица. Для обеспечения репрезентативности выборки все единицы генеральной совокупности должны располагаться в определенном порядке. Если это упорядочение сделано по существенному признаку (который всецело определяет поведение изучаемого показателя), то в выборку идет единица из середины каждой группы.

Если упорядочение сделано по нейтральному признаку, то из каждой группы м.б. отобрана любая единица, но одинаковая.

Для вычисления средней ошибки выборки используются формулы:

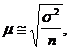
Типическая выборка - часто применяется в статистике торговли. Генеральная совокупность делится на качественно однородные группы. Внутри групп отбираются единицы ◘ в случайном порядке (или механическим способом отбора).

Применяется при изучении сложных статистических совокупностей. Она дает более точные результаты.

При определении ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Средняя из внутригрупповых дисперсий исчисляется:

- для доли альтернативного признака (20)