Свойства степени с целым показателем.

АРИФМЕТИКА

 

Правило сложения и вычитания десятичных дробей:

При сложении (вычитании) десятичные дроби записывают столбиком так, чтобы запятые находились друг под другом. Затем складывают (вычитают) как обыкновенные числа. В ответе –запятую ставят под запятыми.

 

Правило умножения десятичных дробей:

При умножении десятичные дроби перемножают столбиком как обыкновенные числа. В полученном произведении отделяют справа запятой столько цифр, сколько их у перемножаемых дробей вместе взятых.

 

Правило деления десятичных дробей:

При делении преобразуют дробь, на которую делят, в целое число. Для этого в этой дроби сдвигают запятую вправо на нужное количество цифр. Затем в первой дроби сдвигают запятую на то же количество цифр и делят полученное число на целое число.

 

Основное свойство обыкновенной дроби:

Если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, получим дробь равную первоначальной дроби.

 

Правило сложения и вычитания обыкновенных дробей с одинаковыми знаменателями:

При сложении (вычитании) дробей с одинаковыми знаменателями – числители складываются (вычитаются), а знаменатель остается тем же. (Если дроби содержат целую часть, то можно отдельно складывать (вычитать) целые и дробные части).

 

Правило сложения и вычитания обыкновенных дробей с разными знаменателями:

При сложении (вычитании) дробей с разными знаменателями – дроби надо стачала привести к одинаковому знаменателю (используя основное свойство обыкновенной дроби), и только потом складывать (вычитать).

 

Правило умножения обыкновенных дробей:

Чтобы умножить дробь на дробь, надо перемножить их числители (это будет числитель новой дроби) и знаменатели (это будет знаменатель новой дроби). (Если дроби содержат целую часть – то вначале их надо преобразовать в неправильные дроби!)

 

Правило деления обыкновенных дробей:

Чтобы разделить дробь на дробь, надо первую дробь умножить на дробь обратную («переверную») второй. (Если дроби содержат целую часть – то вначале их надо преобразовать в неправильные дроби!)

Правило сравнения обыкновенных дробей:

Из двух дробей с одинаковыми знаменателями, больше та – числитель которой больше. Если дроби с разными знаменателями – то их надо привести к общему знаменателю, а затем сравнивать.

 

Правила сложения чисел с разными знаками:

1) Если в примере два минуса, то в сумме ставим минус, а сами числа складываем

(пример: - 2 – 10 = - (2 + 10) = - 12).

2) Если складываем числа с разными знаками, то в сумме ставим тот знак, который стоит перед бОльшим числом, и из бОльшего числа вычитаем меньшее.

(пример1: -8 + 3 = -5 так как, 8 больше 3, значит в сумме будет знак минус, 8-3=5;

пример2: 20 – 28 = +20 – 28 = - 8, так как 28 больше 20, значит в сумме будет знак минус, 28-20=8; пример3: -5 + 12 = 7. так как 12 больше 5, то в сумме ставим знак плюс, 12-5=7).

 

Правило умножения (деления) чисел с разными знаками:

Если умножить (разделить) числа с одинаковыми знаками, то в результате получим положительное число. Если умножить (разделить) числа с разными знаками, то в результате получим отрицательное число.

 

Основные формулы сокращенного умножения:

(а ± в)² = а² ± 2ав + в²; (а – в) · (а + в) = а² – в²

 

Свойства степени с целым показателем.

Правило/свойство	Формула	Примеры
Чтобы возвести число(выражение) в n-ную степень, над это число(выражение) умножить само на себя n раз	аn =	53 = 5 * 5 * 5 = 125;
Минус в четной степени «исчезает», в нечетной - остается
Любое число(выражение) в 1-ой степени равно самому числу(выражению)	а1 = а	81 = 8; (-17)1 = -17; (2х)1 = 2х
Любое число(выражение) в 0-ой степени равно 1	а0 = 1	120 = 1; (-329)0 = 1; (15xy)0 = 1
Ноль в любой степени равен нулю	0n = 0, где п>0	015 = 0
Единица в любой степени равна единице	1n = 1	165 = 1; 1-48 = 1
При умножении степеней с одинаковыми основаниями, показатели складываются, а основание остается неизменным	an•ak=an+k	52 • 510 = 52+10 = 512 ; х7 • х-3 = 57+(-3) = х4; сk • c8 = ck+8
При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным	или an:ak	28: 23 = 28-3 = 25;
При возведении степени в степень показатели перемножаются	(аn)k = ank	(23)8 = 23*8 = 224; (с6)-5 = с-30; (53)k = 53k
При возведении в степень произведения в эту степень возводится каждый множ итель	(a · b)n = an · b n	(3x2)3 = 33 • (x2)3 = 27x6
При возведении в степень дроби в эту степень возводятся числитель и знаменатель	(a / b)n = an / bn
Чтобы возвести число(выражение) в отрицательную степень (-n) надо 1 разделить на это число(выражение) в степени n
Чтобы возвести в отрицательную степень (-n) обыкновенную дробь, надо дробь «перевернуть» и возводить ее в степень n
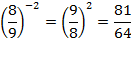
Чтобы возвести в отрицательную степень (-n) десятичную дробь, надо ее вначале записать в виде обыкновенной дроби
Чтобы возвести 10 в n-ную степень, надо за 1 дописать n нулей	107 = 10000000 (семь нулей)
Чтобы возвести 10 в степень (-n), надо перед 1 написать n нулей (первый 0 отделить запятой)	10-7 = 0,0000001 (всего перед 1 семь нулей!)
Чтобы умножить десятичную дробь на 10n, надо перенести запятую на n цифр вправо	15,26894 • 103 = 15268,94
Чтобы умножить десятичную дробь на 10-n, надо перенести запятую на n цифр влево	15,26894 • 10-3 = 0,01526894

ГЕОМЕТРИЯ:

 

Основные свойства треугольника:

1) Сумма углов любого треугольника равна 180°.

2) Внешний угол треугольника равен сумме двух других углов не смежных с ним.

3) Высоты, медианы, биссектрисы и серединные перпендикуляры треугольника пересекаются в одной точке (каждые линии в своей точке!)

4) Медианы треугольника точкой пересечения делятся в отношении 2 к 1 считая от вершины.

5) Центром вписанной в треугольник окружности является точка пересечения биссектрис.

6) Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к его сторонам.

 

7) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.

8) Площадь треугольника равна половине произведения высоты на основание.

 

.

 

Основные свойства равнобедренного треугольника:

А – вершина треугольника АВС!!!

1) Равнобедренный треугольник обладает всеми свойствами обыкновенного треугольника.

2) Углы при основании равнобедренного треугольника равны.

3) Высота, проведенная из вершины равнобедренного треугольника, является так же его биссектрисой и медианой.

4) Высоты, биссектрисы и медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

 

Основные свойства равностороннего (правильного) треугольника:

1) Равносторонний треугольник обладает всеми свойствами обыкновенного и равнобедренного треугольника.

2) Углы равностороннего треугольника равны между собой и равны по 60°.

3) Высота, проведенная из любой вершины равностороннего треугольника, является его биссектрисой и медианой.

4) Высоты, медианы, биссектрисы и серединные перпендикуляры к сторонам равностороннего треугольника пересекаются в ОДНОЙ (общей!) точке.

5) Центры вписанной и описанной около равностороннего треугольника окружностей – совпадают.

Основные свойства прямоугольного треугольника:

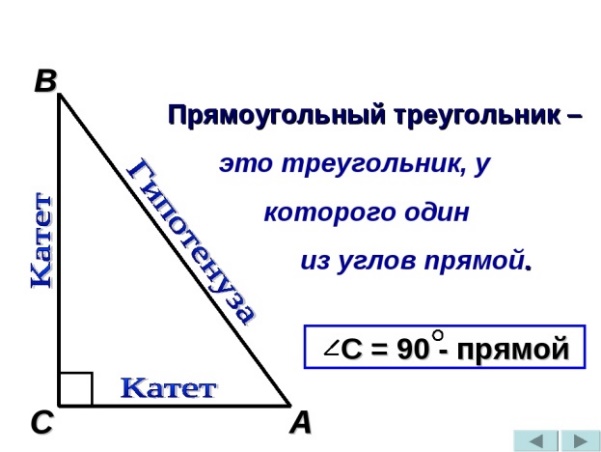
1) Прямоугольный треугольник обладает всеми свойствами обыкновенного треугольника.

2) Сумма острых углов прямоугольного треугольника равна 90°.

3) Катет, лежащей против угла 30°, равен половине гипотенузы.

4) Медиана, проведенная к гипотенузе, равна ее половине.

5) Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, а сама гипотенуза является диаметром этой окружности.

6) Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.

7) Чтобы вычислить синус острого угла прямоугольного треугольника, надо противолежащий катет разделить на гипотенузу.

8) Чтобы вычислить косинус острого угла прямоугольного треугольника, надо прилежащий катет разделить на гипотенузу.

9) Чтобы вычислить тангенс острого угла прямоугольного треугольника, надо противолежащий катет разделить на прилежащий катет.

10) Площадь прямоугольного треугольника равна половине произведения его катетов.

 

Основные свойства параллелограмма:

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.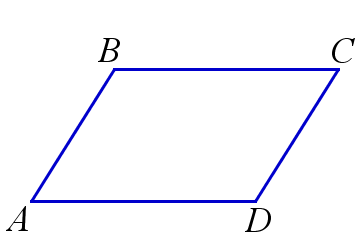

1) Противоположные стороны параллелограмма параллельны и равны.

2) Противоположные углы параллелограмма равны.

3) Сумма всех углов параллелограмма равна 360°.

4) Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

5) Диагонали параллелограмма точкой пересечения делятся пополам.

6) Площадь параллелограмма равна произведению высоты на основание.

Основные свойства ромба:

1) Ромб обладает всеми свойствами параллелограмма.

2) Диагонали ромба перпендикулярны между собой.

3) Диагонали ромба делят его углы пополам (являются биссектрисами углов).

4) Площадь ромба равна половине произведения его диагоналей.

 

Основные свойства прямоугольника:

1) Прямоугольник обладает всеми свойствами параллелограмма.

2) Все углы прямоугольника равны по 90°.

3) Диагонали прямоугольника равны.

4) Площадь прямоугольника равна произведению его смежных сторон (высоты на длину).

 

Основные свойства квадрата:

1) Квадрат обладает всеми свойствами параллелограмма и ромба.

2) Все стороны квадрата равны и все углы равны по 90°.

3) Площадь квадрата равна квадрату его стороны.

 

Основные свойства трапеции:

Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет. Параллельные стороны называются – основания, а непараллельные стороны называются боковыми сторонами.

1) Сумма углов трапеции равна 360°.

2) Сумма углов, прилежащих к боковой стороне трапеции, равна 180°.

3) Площадь трапеции равна полу-сумме оснований, умноженной на высоту.

 

Основные свойства равнобедренной трапеции:

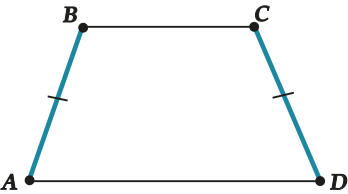
Если боковые стороны равны, то она называется равнобедренной, или равнобокой.

1) Равнобедренная трапеция обладает всеми свойствами обыкновенной трапеции.

2) Углы при основаниях равнобедренной трапеции равны.

3) Диагонали равнобедренной трапеции равны.