Введение.
В этой лекции будут рассмотрены следующие 4 вопроса.
1. Размещения.
2. Перестановки.
3. Сочетания.
4. Бином Ньютона.
Комбинаторика, или дискретная математика, изучает конечные множества для подсчета количества элементов, обладающих заданными свойствами. В настоящее время получила мощное развитие в связи с применением в теории автоматов.
Цель занятия: знать и уметь использовать бином Ньютона.
1. Размещения
Определение 1. Группы, составленные из каких-либо предметов, называются соединениями.
Определение 2. Размещениями из n элементов по p называются такие соединения, из которых каждое содержит p элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.
Примеры.
Из одного элемента можно составить лишь одно размещение.
Из двух элементов а и b можно составить два размещения по одному элементу и два размещения по два элемента ab и ba.
Из трех элементов а, b и c можно составить три размещения по одному элементу; шесть размещения по два элемента ab, ba, ac, bc, ca, cb; шесть размещений по три элемента abc, bac, acb, bca, cab, cba и т.д.
Число размещений из n элементов по p в каждом будем обозначать символом 
.
Пусть имеется n элементов a, b, c, …,h, k, l. Очевидно, что размещений из n элементов по одному будет n.
. (1)
Составим размещения по два.
ab; ac; …..ah; ak; al;
ba; bc; …..bh; bk; bl;
ca; cb; …..ch; ck; cl;
……………………..
……………………..
la; lb; …...lh; lk.
Число размещений в каждой строке равно n-1, а число всех строк n. Следовательно,
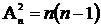(2)
Число размещений по три будет равно
(3)
Пользуясь методом математической индукции можно показать справедливость формулы
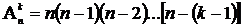(3)
Предположим, что формула (3) выполняется, докажем, что тогда будет выполняться и равенство
Возьмем одно из размещений (3) k-го порядка и станем присоединять к нему по очереди каждый из оставшихся 
элементов, не вошедших во взятое нами размещение. Тогда мы получим размещений 
порядка.
Таким способом из каждого размещения k-го порядка можно образовать размещений -го порядка.
Но число всех размещений k-го порядка по нашему предположению равно произведению
Следовательно, из всех размещений k-го порядка можно составить указанным способом столько размещений -го порядка, сколько единиц окажется в произведении
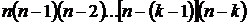
Легко понять, что изложенным способом получим все размещения -го порядка, взятые только по одному разу. Поэтому окажется, что
.
Таким образом, из предположения, что формула (3) верна для p=k, мы пришли к тому, что формула оказывается верной при p=k+1. Но поскольку формула (3) верна при p=1, то значит она верна всегда, т.е. при любом натуральном значении p, меньшем или равном n.
Примеры.
;
;
;
.
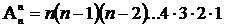Из последних двух формул следует, что
.
2. Перестановки
Определение 3. Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
Из одного элемента можно составить лишь одну перестановку.
Из двух элементов а и b можно составить две перестановки ab и ba.
Из трех элементов а, b и c можно составить шесть перестановок abc, bac, acb, bca, cab, cba и т.д.
Число перестановок из n элементов обозначается символом 
.
Число перестановок из n элементов – это то же самое, что число размещений из n элементов по n в каждом. Поэтому
,
или
. (4)
Пример.
Сколькими различными способами могут разместиться на скамейке 10 человек?
Произведение n натуральных чисел обозначается сокращенно n!, т.е.
! (читается n факториал)
Формулу числа перестановок теперь можно записать так:
!
Умножив и разделив произведение
на !, получим:
.
Принимается, что 0!=1
3. Сочетания
Определение 4. Сочетаниями из n элементов по p называются такие соединения, из которых каждое содержит p элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Примеры.
Из одного элемента можно составить лишь одно сочетание.
Из двух элементов a, b можно составить два сочетания по одному элементу и лишь одно сочетание по два элемента ab.
Из ьрех элементов a, b, c можно составить:
3 сочетания по одному элементу:
A, b, c
3 сочетания по два элемента:
Ab, bc, ac
одно сочетание по три элемента:
Abc.
И т. д.
Число сочетаний из n элементов по p обозначается символом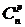 
.
Если в каждом сочетании из n элементов по p сделать всевозможные перестановки, тот образуются всевозможные размещения из n элементов по p. Поэтому
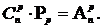
Отсюда
или
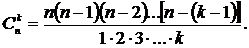(5)
Пример. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов.
.
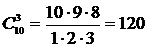Умножим числитель и знаменатель правой части формулы (5) на произведение 
. Тогда получим
или
или
(6)
Первое свойство сочетаний:
.
Доказательство:
и 
.
Отсюда
.
Второе свойство сочетаний:
Доказательство:
4. Бином Ньютона.
Очевидно, что
, так как 
;
, так как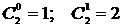 
; 
Пусть верна формула
(7)
Умножим обе части этого равенства на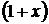 
.
Тогда получим:
=
,
т.е.
Пользуясь формулой
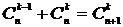
и приняв во внимание, что
и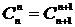 
получим окончательно
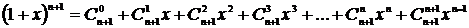
Из предположения, что формула верна при n, пришли к выводу, что формула верна при n+1.
Возьмем
или
(8)
Свойства биномиальных коэффициентов.
1.Биномиальные коэффициенты, равноудаленные от начала и конца разложения равны между собой.
.
2. 
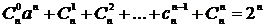
полагая в равенстве (8) a=b=1, получаем искомое равенство
3. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Полагая в равенстве (8) a=b= -1, получаем искомый результат
Биномиальные коэффициенты можно получить из треугольника Паскаля
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
……………………………………………….
…………………………………………………….
- я строка этой таблицы дает биномиальные коэффициенты разложения n-ой степени бинома.
Контрольные вопросы по теме занятия:
1. Что называется размещениями?
2. Что называется перестановками?
3. Дайте пример применения бинома Ньютона.
Заключение.
Представим содержание лекции в виде следующей схемы.
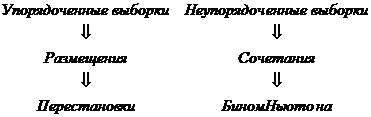
Важнейшей формулой математики является бином Ньютона, для закрепления которой необходимо самостоятельно проверить его для нескольких невысоких показателей.