ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ЭЛЕМЕНТЫКОМБИНАТОРИКИ
Во многих задачах классической теории вероятностей используется комбинаторика, т. е. раздел математики, в котором изучаются различные соединения (комбинации) элементов конечных множеств.
Многие комбинаторные задачи могут быть решены с помощью двух правил – правила умножения и правила сложения
Теорема 1. Правило умножения: если из некоторого конечного множества первый объект (элемент а) можно выбрать n1 способами, а второй объект (элемент b) – n2 способами, то оба объекта (a и b)в указанном порядке можно выбрать n1 * n2 способами.
Этот принцип распространяется на случай трех и более объектов.
Теорема 2. Правило сложения: еслинекоторый объект а можно выбрать n1 способами, а объект b можно выбрать n2 способами, причем первые и вторые способы не пересекаются, то любой из объектов (а и b) можно выбрать n1 + n2 способами.
Это правило распространяется на любое конечное число объектов.
Существуют две схемы выбора элементов из заданного множества: без возвращения, когда выбранные элементы не возвращаются в исходное множество, и с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.
Схема выбора без возвращений
Пусть дано множество, состоящее из n различных элементов.
Размещением из п элементов по k элементов (0<= k <= п) называется любое
упорядоченное подмножество данного множества, содержащее k элементов
Два размещения различны, если они отличаются друг от друга либо составом элементов, либо порядком их расположения.
Число размещений из п элементов по k обозначаются символом и вычисляется по формуле

Перестановкой из п элементов называется размещение из п элементов по п элементов.
Таким образом, указать ту или иную перестановку данного множества из п элементов значит выбрать определенный порядок этих элементов. Поэтому любые две перестановки отличаются друг от друга только порядком следования элементов.
Число перестановок из п элементов обозначается символом и вычисляется по формуле
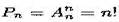
Сочетанием из п элементов по k элементов (0<= k <= п) называется любое подмножество данного множества которое содержит k элементов.
Любые два сочетания отличаются друг от друга хотя бы одним элементом
(т. е. отличаются только составом элементов).
Число сочетаний из п элементов по k обозначается символом и вычисляется по формуле

Для чисел С (они называются биномиальными коэффициентами) справедливы следующие тождества:

Схема выбора с возвращением
Если при упорядоченной выборке k элементов из п элементы возвращаются обратно, то полученные выборки представляют собой размещения с повторениями. Число всех размещений с повторениями из п элементов по k обозначается символом и вычисляется по формуле

Если при выборке k элементов из п элементы возвращаются обратно без последующего упорядочивания (таким образом, одни и те же элементы могут выниматься по нескольку раз, т. е. повторяться) то полученные выборки есть сочетания с повторениями. Число всех сочетаний с повторениями из п элементов по k обозначается символом и вычисляется по формуле

Пусть в множестве из п элементов есть k различных типов элементов, при
этом 1-й тип элементов повторяется п1 раз, 2-й – п2 раз, … k -й – пk раз, причем п1 + п2 + … + пk = п. Тогда перестановки элементов данного множества представляют собой перестановки с повторениями.
Число перестановок с повторениями (иногда говорит о числе разбиений
множества) из п элементов обозначается символом Рn(п1 , п2, … пk) и вычисляется по формуле

Итоговая сводка формул приведена в следующей таблице.
(1- строка - без повторений 2-я строка — с повторениями)

1.1. Сколько различных трехзначных чисел можно составить из
цифр 0, 2, 3, 5, 7если: а) цифры не повторяются; б) цифрымогут повторятся?
О а)Первую цифру можно выбрать четырьмя способами (числа вида
025, 073,.. не считаем трехзначными). Выбрав первую цифру (например, цифру 5),вторую цифру можно также выбрать четырьмя способами (второй цифрой может быть любая из оставшихся 0 2, 3, 7). Третью цифру, очевидно, можно выбрать тремя способами. Следовательно, согласно правилу умножения имеется 4 * 4* 3 = 48 способов расстановки цифр, т е. искомых трехзначных чисел будет 48 (вот некоторые из них: 500, 237, 530, 702, 523, …).
б) Понятно, что если цифры могут повторяться, то трехзначные числа можно составить 4*5*5 = 100 способами (вот некоторые из них: 222, 200, 332,..).
1.2. Сколько чисел, содержащих не менее трех попарноразличных цифр можно составить из цифр 2, 4, 6, 8, 9?
О По правилу умножения трехзначных чисел можно составить 5*4*3 = 60 способами, а четырехзначных — 5*4*3*2 = 120 способами, столько же пятизначных чисел (5*4*3*2*1). По правилу сложения всего можно составить 60 + 120 + 120 = 300 чисел, состоящих не менее чем из трех попарно различных цифр.
1.3. Сколькими способами могут быть распределены три призовых места среди 16 соревнующихся?
1.4. В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать двух студентов одного пола?
1.5. Если подбросить одновременно три игральные кости то сколько имеется различных возможных комбинаций выброшенных очков?
1.6. В цветочном киоске 7 видов цветов. Сколькими разными способами можно составить букет, содержащий 3 цветка?
1.7. Из пункта А в пункт В можно добраться самолетом, поездом, автобусом а из него в пункт С — пешком, на тракторе, на лошади, на лодке. Сколькимиспособами можно выбрать дорог от пункта А до пункта С через В?
1.8. Сколькимиспособами можно выбрать один цветок из корзины, в которой имеется 12 гвоздик, 15 роз и 7 хризантем?
1.9. Составить различные размещения по два элемента из элементовмножества А (3, 4, 5) и подсчитать их число.
О Из трех элементов можно образовать следующие размещения по два элемента: (3, 4); (4, 3); (3, 5); (5, 3); (4, 5); (5, 4).Таким образом, всех их 6. Однако число размещений можно подсчитать и по формуле (1):

1.10. Сколькими способами 3 награды (за I, II, III места) могут быть
распределены между 10 участниками соревнований?
О Будем считать, что каждый участник соревнований может получить
не более одной награды. Выбрать 3-х участников соревнований из 10 можно
 способами, так как призовые тройки отличаются друг от друга либо составом участников, либо порядком их следования.
способами, так как призовые тройки отличаются друг от друга либо составом участников, либо порядком их следования.
Этот же результат можно получить, применяя правило умножения: претендентов на главную награду (за 1 место) 9; на вторую — 8; на третью 7; число различных способов распределения наград равно 10*9*8 = 720.
1.11. Сколько имеется пятизначных чисел, все цифры у которых
различны?
1.12. Сколькими способами можно составить трехцветный полосатый флаг (три горизонтальных полосы), если имеется материя 5различных цветов?
1.13. Из группы в 15человек выбирают 4-х участников эстафеты
800 х 400 х 200 х 100. Сколькими способами можно расставить спортсменов на этих этапах?
1.14. Составить различныеперестановки из элементов множества
А {5; 8; 9}.
О По формуле (2)число перестановок из 3-х элементов равно Р3 = 3! = 1*2*3 = 6, Составляем их: (5, 8, 9); (5, 9, 8); (8, 9, 5); (8, 5, 9); (9, 5, 8);(9, 8, 5).
1.15. Сколькими способами можно расставить на книжной полке десятитомникпроизведений Д. Лондона, располагая их: а) в произвольном порядке; б) так чтобы I, V и IХ тома стояли рядом (в любом порядке); в) так, чтобы I, II, III тома не стояли рядом (в любом порядке).
О а) Число способов расстановки 10 книг равно числу перестановок из
элементов: Р10 = 10! = 3 628 800.
б) Мысленно связав I, V и IХ тома или положив в один пакет, получим 8 книг, т. е, 7 книг и 1 связку (или пакет) книг. Их можно расставить на полке = 8! способами. Каждому из этих способов расстановки соответствуют Рз = 3! способов расстановки книг, находящихся в связке (I, V и IХ тома по-прежнему стоят рядом, но в ином порядке). Согласно правилу умножения, число возможных расстановок 10 книг на полке так, чтобы 3 определенные книги (I, V и IХ тома) стояли рядом равно Р8 * Р3 =8! * 3! = 40320 * 6 = 241920.
в) Искомое число способов расстановки книг, с учетом пунктов а) и 5), равно Р10 — Р8 * P3 = 3 628 800 - 241 920 = 3 386 880.
1.16. В комнате имеется 7 стульев. Сколькими способами можно разместить па них 7гостей? 3 гостя?
1.17. Студенты дают 5 экзаменов, в том числе 2 экзамена по математике. Сколькими способами можно распределить экзамены но так, чтобыэкзамены по математике следовали один за другим? Не следовали один за другим?
1.18. Сколько различных слов можно получить, переставляя буквы в слове:
а) СОЛНЦЕ; б) ТЕАТР; в) ЛИЛИ; г) SOS?
1.19. Сколькими способами можно упорядочить множество А = {8, 9, 10, 11,..., 15} так, чтобы каждое четное число имело четный номер?
1.20. Составить различные сочетания по два из элементов множества А {3, 4, 5} и подсчитать их число
О Из трех элементов можно составить следующие три сочетания по два
элемента: {3, 4}; {3, 5}; {4, 5}.Их число можно подсчитать к по формуле (3):

6.1.21. Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькимиспособами онможет выб рать приглашенных?
О Так как для Владимира важен только состав гостей (порядок роли не играет), то число способов выбора троих гостей из 7 можно найти по формуле сочетаний (3) 
1.22. В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее а) 3 гвоздики; б) б гвоздик одного цвета; в) 4 красных и 3 розовых гвоздики?
О а) Так как порядок выбора цветов не имеет значения то выбрать гвоздики из вазы, в которой стоят 16 гвоздик можно С способами по формуле (3) находим: 
б) Выбрать б гвоздик красного цвета можно 84 способами а 6
гвоздик розового цвета = 7 способами. По правилу сложения выбрать б гвоздик одного цвета (красных или розовых) можно  = 84 + 7 = 91 способом.
= 84 + 7 = 91 способом.
в) Выбрать 4 красных гвоздики из 9 имеющихся можно С способами, а 3 розовых из имеющихся 7 можно С способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения  способами
способами
1.23. Сколькими способами можно разбить 8 предметов на две равные (по количеству предметов) группы?
1.24. Группа шахматистов сыграла между собой 28 партий. Каждые два из них встречались между собой один раз. Сколько шахматистов участвовало в соревновании?
1.25. Группа туристов из 12 юношей и 7 девушек выбирает по жребию 5 человек для приготовления ужина. Сколько существует способов, при которых в эту «пятерку» попадут:
а) одни девушки; б) 3 юноши и 2 девушки; в) 1 юноша и 4 девушки; г) 5 юношей?
1.26. Сколькими способами можно разбить 9 предметов на 2 группы (выбор одной группы однозначно определяет вторую)?
1.27. Пять авторов должны написать задачник по математике, состоящий из 14 глав. Два автора напишут по 2 главы два других по 3 и еще один 4 главы книги. Сколькими способами может быть распределен материал между авторами?
1.28. В ящике 15 деталей среди которых 6 бракованных. Наудачу
выбирается комплект из 5 деталей. Сколько всего комплектов, в каждом из которых 2 детали бракованные?
1.29. Из элементов (цифр) 2, 4, 5 составить все размещения и сочетания с повторениями по два элемента,
О Размещения с повторениями по два элемента таковы (2, 2); (2, 4); (2, 5); (4, 4); (4, 5); (4, 2); (5, 5); (5,2); (5,4). Их число можно вычислить и по формуле (4): 
Сочетания с повторениями по два элемента таковы (в отличие от размещений здесь порядок элементов в выборке не имеет значения, т е. например пары (2, 4) и (4, 2) не различаются): (2,2); (2, 4); (2, 5); (4, 4); (4, 5); (5, 5).. Их число можно вычислить и по формуле (5): 
1.30. В магазине имеется 7 видов тортов. Сколькимиспособами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?
О Поскольку порядок расположения торгов в наборе не играет роли, то искомое число наборов равно числу сочетаний с повторениями из 7 элементов по 3 в каждом. По формуле (5) имеем  (см. также задачу 6.1.6).
(см. также задачу 6.1.6).
Если имеется 3 вида тортов, а нужен набор из 7тортов, то число возможных наборов равно 
1.31. Пять человек вошли в лифт 1-м этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
О Каждый из 5 пассажиров может выйтина любом из восьми этажей со 2-го по 9-й включительно. Возможными вариантами их выхода являются, например 2—3—5—5—5 (это значит что на 2-м этаже вышел один пассажир, на 3-м — один, а трое вышли на 5-м этаже) или 9—9—9—9—9 или 4—5—6—7—9, и т.д. Общее число выходовпассажиров, по формуле (4) равно 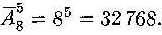
Этот же результат можно получить, используя правило умножения: для 1-го пассажира имеется 8 вариантов выхода на этаже, для 2-го тоже 8 и для 8-го — 8, и для 4-го – 8 и для 5-го — 8. Всего получается 8*8*8*8*8 = 85 вариантов выхода 5-ти пассажиров.
1.32. Сколько различных слов (под «словом» понимается любая комбинация букв) можно составить, переставляя буквы в слове АГА? MISSISSIPPI?
О Вообще из трех букв можно составить Рз = 3! = 6 различных трехбуквенных слов. Вслове АГА буква А повторяется,аперестановка одинаковых букв не меняет «слова». Поэтому число перестановок с повторениями меньше числа перестановок без повторений во столько раз, сколько можно переставлять повторяющиеся буквы. В данном слове две буквы (1-я и 3-я) повторяются; поэтому различных трехбуквенных «слов»