Значит, в данном случае вместо полинома

следует использовать полином При x₁=x₂=…=x_n=1 производящая функция имеет вид:

Задача. Даны элементы

х₁; х₁, х₂, х₂, х₃

n₁=2, n₂=2, n₃=1

Подсчитаем количество перестановок длины 3 из этих элементов. k = 3.

=[выпишем коэффициенты только при t³, т.к. к=3]=

=

Для подсчета числа перестановок длины k из n элементов, среди которых есть повторяющиеся, используем производящую функцию:

Чтобы найти требуемое число перестановок длины вычисляем коэффициент при t^k, положив х_j=1, j=1,l

В формуле:

х_j, j= - элементы n- элементного множества, которые могут повторяться, образуя при этом l групп.

n_j – количество элементов вида х_j, j=

n₁+n₂+…+n_l=n

Например, имеем набор элементов (5 штук):

x₁x₁x₂x₂x₃ n₁=2, n₂=2, n₃=1

Чтобы подсчитать количество перестановок длины 3 из этих элементов, воспользуемся производящей функцией:

=[выпишем коэффициенты только при t³, т.к. к=3]=

означает, что элемент каждого вида входит в перестановку длины 3 по 1 разу

означает, сто х1 входит в перестановку 2 раза, х2 – 1 раз, а х3 – не входит в перестановку длины 3

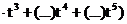=[т.к. нас интересует количество таких перестановок, то полагается x_j, j= ]= =[выпишем только коэффициент при t³]=

= - количество постановок длины 3 из элементов заданного множества.

Действительно, выпишем возможные варианты:

х₁х₁х₂ х₁х₂х₁ х₂х₁х₁ } получить все перестановки из х₁, х₁ и х₂ - способов, т.к. 2 элемента одинаковы

х₁х₂х₂ х₂х₁х₂ х₁х₂х₂ } способов

х₁х₂х₃ х₁х₃х₂ х₂х₁х₃ х₂х₃х₁ х₃х₁х₂ х₃х₂х₁ } 3! способа

х₃х₁х₁ х₁х₃х₁ х₁х₁х₃ } способа

х₃х₂х₂ х₂х₃х₂ х₂х₂х₃ } способа

Всего – 18 перестановок.

 

Метод включения и исключения.

Рассмотрим задачу: В результате опроса: 67 человек выяснилось, что 47 из них знают английский язык, 35 - немецкий язык и 23 оба языка. Сколько человек из опрошенных не знают ни английского, ни немецкого?

Решение. Разобьем множество опрошенных людей на части, не имеющие общих элементов, следующим образом:

1 - ая часть: те, кто знает только английский: 47 - 23 = 24

2 - ая часть: те, кто знает только немецкий: 25 - 23 = 12

3 - ая часть: те, кто знает оба языка: 23.

4 - ая часть: те, кто не знает ни одного из этих языков: 67 - (4 + 12 + 23) = 8.

Полученный ответ запишем в виде: 8 = 67 - (24 + 12 + 23).

Перепишем равенство, используя в первой части только числа, данные в задаче:

8 = 67 - 23 - (47 - 23) - (35 - 23) = 67 - 47 - 35 + 23.

Теперь видна закономерность: из общего числа сотрудников вычитается число знающих английский и число знающих немецкий. При этом некоторые сотрудники попадают в оба списка и оказываются “вычтенными” дважды (те: кто знает оба языка). Прибавляя их число, мы получаем число опрошенных, не знающих ни одного из этих языков.

 

Усложним задачу, добавив еще один язык. Чтобы выявить число лиц, не владеющих ни одним из указанных иностранных языков, сначала из общего числа опрошенных лиц, знающих одни языки и может быть, другие. При этом некоторые лица оказываются вычтенными дважды, поскольку знают два языка. Поэтому прибавляют числа, показывающие, сколько человек владеют двумя языками и, может быть, еще третьим. Но лица, владеющие тремя языками, оказываются сначала трижды вычтенными, а потом трижды прибавленными. Так как их все-таки надо вычесть из общего числа опрошенных, то приходится еще отнять число лиц, владеющих одновременно тремя языками.

 

Сформулируем общий закон.

Пусть имеется N и n свойств α_1, α₂,…, α_n. Каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими свойствами. Обозначим через

N(α_i α_j…α_k) количество предметов, обладающих свойствами α_i, α_j,…,α_k (и, может быть, еще некоторыми из других свойств).

 

Если необходимо подчеркнуть, что берутся элементы, заведомо не обладающие некоторым свойством, то это свойство пишем с чертой. Например, через N(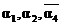) обозначено количество элементов, обладающих свойствами , но не обладающих свойствами (вопрос о наличии других свойств остается открытым).

 

Число элементов, не обладающих ни одним из указанных свойств, обозначается через N().

Общий закон состоит в том, что

.

 

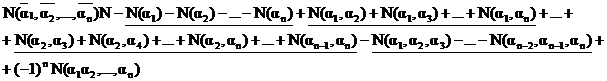2 Здесь алгебраическая сумма распространена на все сочетания свойств из множества {α₁, α₂,…, α_n}, причем знак + ставится, если число учитываемых свойств четно, и знак -, если это число нечетно. Например: N(α₃ α₄ α₁₀) входит со знаком -, N(α₁ α₃ α₆ α₈) - со знаком +.

Формула (*) называют формулой включений и исключений: сначала исключаются все предметы, обладающие хотя бы одним из свойств α₁, α₂,…, α_n, потом включаются предметы, обладающие по крайней мере двумя из этих свойств, исключаются имеющие по крайней мере три и так далее.

Пример (задача решается по формуле включений и исключений)

Сколько чисел в первой сотне не делится ни на одно из чисел 2, 3, 5?.

Решение. Обозначим через α₁ свойство числа делится на 2, через α₂ - свойство делимости на 3 и через α₃ - свойство делимости на 5. Тогда α₁ α₂ означает, что число делится на 6, α₁ α₃ означает, что оно делится на 10, α₂ α₃ - что оно делится на 15. α₁ α₂ α₃ означает, что число делится на 30. Надо найти, сколько чисел не обладают ни одним из свойств α₁, α₂, α₃. По формуле (*) имеет:

Но чтобы найти, сколько чисел от 1 до N делится на n, надо разделить N на n и взять целую часть получившегося частного.

Поэтому N(α₁)=50, N(α₂)=33, N(α₃)=20, N(α₁ α₂)=16, N(α₁ α₃)=10, N(α₂ α₃)=6, N(α₁ α₂ α₃)=3.

Значит, , от 1 до 100 не делится ни на 2, ни на 3 ни на 5.

 

 

В 92 - процессорной ЭВ системе 19 микропроцессоров обрабатывает текстовую информацию, 17 - графическую, 11 - символьную, 12 - микропроцессоров одновременно обрабатывает графическую и текстовую, 7 - текстовую и символьную, 5- графическую и символьную, а часть микропроцессоров одновременно обрабатывает графическую, текстовую и символьную информацию. Сколько микропроцессоров является универсальными, если при решении задач не задействовали 67 микропроцессоров.

 

Экстремальные комбинаторные задачи.

Существуют 3 типа комбинаторных задач:

1) задачи, в которых подсчитывают число решений;

2) задачи, в которых решается вопрос о существовании решения;

3) задачи, которые из некоторой совокупности выделяют элемент, обладающий определенным свойством в максимальной или минимальной степени - экстремальные задачи.

В экстремальных комбинаторных задачах ищется экстремум некоторой целочисленной функции, заданной на конечном дискретном множестве, или элементы этого множества, в которых функция принимает экстремальные значения.

 

Операции применяемые для решения экстремальных комбинаторных задач, - это получение значений функции F, их перебор, сравнение и выделение из них min и max.

Для решения ЭКЗ разработано много методов.

Общая идея этих методов состоит в замене полного перебора всех вариантов частичными переборами меньших объемов.

Для этого отбрасываются некоторые подмножества, заведомо не содержащие искомого экстремума.

Один из таких методов – метод ветвей и границ.

Идея метода:

- множество разбиваем на подмножество;

- на каждом из полученных подмножеств оцениваем значение целевой функции, то есть той величины, чей экстремум (min, max) нужно найти;

- подмножество, на котором оценка наилучшая, в свою очередь тоже разбивается на подмножество. Оценивая каждое из этих подмножеств, опять выбираем наилучшее.

Сделанные для каждого подмножество оценки и найденные экстремальные значения позволяют отбросить те подмножества, где заведомо экстремума нет.

 

Примеры экстремальных комбинаторных задач.

К ЭКЗ относятся задача о рюкзаке и задача о назначениях.

1. Задача о рюкзаке.

Имеется n предметов, веса которых равны p₁, p₂,…, p_n, а ценность – c₁, c₂,…, c_n.

Требуется заполнить рюкзак, обладающий заданной вместимости R, таким набором предметов, который обладал бы наибольшей ценностью.

Составляется вектор X=(x₁, x₂,…,x_n), где x_i=1, если i-й предмет должен быть помещён в рюкзак, и x_i=0 в противном случае,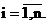

Задача: Найти max 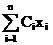(максимальную ценность вложенных предметов), при условии, что .

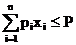Пример: С=5х₁+4х₂+6х₃+2х₄+3х₅ х_iÎ{0,1} (1)

2х₁+2х₂+х₃+2х₄+х₅£5

Всевозможных наборов (х₁, х₂, х₃, х₄, х₅), на которых функция С может принимать значения без учета ограничений – 2⁵ (это векторы из 0 и 1 размерности 5).

Найти решение такой задачи достаточно тяжело. Легче найти решение задачи, где х_i не просто принимает значение 0 или 1, а находиться в промежутке 0 £ х_i £ 1. Но при этом максимум может увеличиться.

Для того, чтобы оценить максимальное значение функции С, решим аналогичную задачу, в которой вместо условия х_iÎ{0,1} будет условие х_iÎ[0,1].

С=5х₁+4х₂+6х₃+2х₄+3х₅ 0 £ х_i £ 1 (2)

2х₁+2х₂+х₃+2х₄+х₅£5

Поскольку множество, на котором ищется max, увеличилось, то максимальное значение С в новой задаче будет ³ max, значения С в исходной задаче. Таким образом, решив вторую задачу, мы сможем оценить максимум значений С в первой задаче.

 

Составим таблицу:

i	Сi	pi	Сi/pi
			2,5
5

ценность вес ценность на единицу веса

 

 

1. Считаем ценность на единицу веса для каждого предмета: С_i/p_i.

2. Устанавливаем очередность укладывания предметов в рюкзак – начиная с наибольшей С_i/p_i.

3. Укладываем в рюкзак предметы в порядке убывания С_i/p_i до тех пор, пока после укладывания очередного предмета (с номером i) вес рюкзака не превысит допустимую величину.

Если вес рюкзака стал больше допустимой величины, то отрезаем от последнего взятого предмета лишнюю часть.

То есть, полагаем х_i=1, если мы берем i-й предмет, х_i=0, если не берем i-й предмет, и х_iÎ[0,1], если берем часть предмета.

 

i	хi	Сi	pi
	1/2		4/2

 

 

значит решение (максимальное значение целевой функции С£16)

4. Вычисляем значение функции С на полученном наборе х_i и записываем его как оценку решения: 6 + 3 + 5 + 2 = 16, следовательно, самое лучшее решение будет £16.

5. Разбиваем множество всех наборов х_i на два подмножества:

Первое подмножество содержит только те наборы, в которых х₃=1, второе – наборы, в которых х₃=0.

При разбиении х_i будем брать для рассмотрения в порядке убывания С_i/p_i.

6. Переходим к пункту 3 с учетом особенности подмножеств:

 

Переходим к пункту 3 с учетом особенностей подмножеств.

х₃=0

i	хi	Сi	pi
			=12

точное значение (равенство), т.к. х_iÎ{0,1}

 

х₃=1

i	хi	Сi	pi
	1/2
			£16

точное значение (равенство), т.к. х_iÎ[0,1]

 

 

 

 

 

На таких наборах мы сможем получить значения ЦФ, больше 12.

х3=1	i	хi	Сi	pi
х5=0
				=12

точное значение (равенство), т.к. х_iÎ{0,1}

 

х3=1	i	хi	Сi	pi
х5=1
х1=0
		1/2
				£14

оценка

 

х3=1	i	хi	Сi	pi
х5=1
х1=1
х2=1
			2?
			>5

нет решений

 

На таких наборах мы сможем получить значения ЦФ, больше 12.

х3=1	i	хi	Сi	pi
х5=1
		1/2
				£16

оценка

 

х3=1	i	хi	Сi	pi
х5=1
х1=1
		1/2
				£16

оценка

 

х3=1	i	хi	Сi	pi
х5=1
х1=1
х2=0
		1/2	1/2
				£15

оценка

 

Мы получим, что максимум целевой функции при заданном ограничении не может быть больше 15 ни на каком наборе.

В процессе решения мы нашли один набор предметов, ценность которого равна 15 и вес равен 5. Все наборы искать не требуется. Поэтому задача считается решенной.