Сочетаниями из n элементов по k элементов с повторениями называются кортежи,
содержащие k элементов, причём каждый элемент принадлежит к одному из n типов. Число таких сочетаний обозначается 
Например, из трёх элементов a,b,c можно составить такие сочетания по два с повтореними(n =3, k =2):
aa,ac,bc,ab,bb,cc.
Поставим в соответствие каждому приведённому кортежу (сочетанию) последовательность
из нулей и единиц, придерживаясь такого правила: пишется подряд столько единиц,сколько элементов первого типа входит в данный кортеж, далее ставим нуль и после него записываем столько единиц, сколько элементов второго типа содержит этот кортеж и т.д. Таким образом нулями отделяем единицы, соответствующие элементам одного типа, а также нули означают отсутствие в кортеже элементов других типов. Сумма единиц равна k. Записанным выше кортежам соответствуют такие последовательности:
1100,1001,0101,1010,0110,0011.
Таким образом, каждому сочетанию из n по k соответствует последовательность из k единиц и n -1 нулей. По полученным последовательностям также можно однозначно восстановить сочетания. Число перестановок из k единиц и n -1 нулей, а это и есть число сочетаний с повторениями, равно:
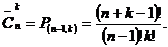
Эту же формулу, пользуясь свойствами сочетаний, можно записать в виде:
Сочетания без повторений
Сочетаниями без повторений из n различныхэлементов по k являются кортежи длиной k, содержащие k элементов, рассматриваемые без учёта их порядка. Так как имеем дело с неповторяющимися элементами, то проще использовать язык множеств. Сочетанием из n элементов по k называется произвольное неупорядочное k- элементное подмножество множества, состоящего n различныхэлементов. Все эти образованные подмножества должны отличаться друг от друга хотя бы одним новым элементом. Общее число таких сочетаний обозначается через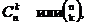 
причём обязательно k≤n.
Для вывода формулы, определяющей число сочетаний, воспользуемся примером. Из множества (a,b,c,d) образуем трёхэлементные подмножества, отличающиеся друг от друга составом элементов и запишем их в левой части таблицы, а в правой части все перестановки каждого сочетания:
| Сочетания | Перестановки |
| abc | abc, acb, bac, bca, cab, cba |
| abd | abd, adb, bad, bda, dab, dba |
| acd | acd, adc, cad, cda, dac, dca |
| bcd | bcd, bdc, cbd, cdb, dbc, dcb |
Видно, что каждому сочетанию соответствует шесть перестановок. Действительно, Р3 =3!=6, т.е. любое трёхэлементное подмножество можно переставить 3! способами. В результате получаем 24 размещения. Отсюда можно для данного примера записать соотношение: 
или
 |
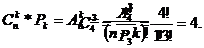Обобщая данное рассуждение, можно найти общую формулу числа сочетаний из n различныхэлементов по k:
 |
Разделив обе части равенства на Pk,получим:
Свойства сочетаний
1. 
2. 
3. 
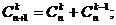(Правило Паскаля)
4. 
;
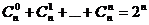5. 
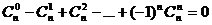
Бином Ньютона
Эти равенства образуют биномиальную теорему. Выражения 
называют биномиальными коэффициентами. Разложение двучлена (a +b)n называют биномом Ньютона, хотя это не является справедливым, так как это разложение было уже известно среднеазиатским математикам ещё в ХI веке. Но заслугой Ньютона является то, что он обобщил эту формулу для нецелого показателя n.
Разложение двучлена (a +b)n можно записать в свёрнутом виде:
 |
Если │ nb │мало, то (1+ b) n ≈1+ nb. (Биномиальное приближение).
Принцип сложения
Каждое действие допустимо отдельно, они не могут быть выполнены одновременно. Дело обстоит так: или это действие или то действие. Такие действия взаимно исключают одно другое. Их нельзя выполнить вместе. Каждое действие образует свою отдельную задачу, и окончательный результат получается сложением, а не умножением.
Принцип сложения
Каждое действие допустимо отдельно, они не могут быть выполнены одновременно. Дело обстоит так: или это действие или то действие. Такие действия взаимно исключают одно другое. Их нельзя выполнить вместе. Каждое действие образует свою отдельную задачу, и окончательный результат получается сложением, а не умножением.