Кодовые слова заданной длины
Пусть алфавит 
, тогда множество различных двухбуквенных кодовых слов
,
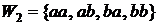а множество трехбуквенных кодов
.
Количество кодовых слов длины r в алфавите численностью n обозначается 
(читается «а из эн по эр»). Очевидно, что это количество зависит от численности алфавита и от длины слова.
Теорема. Количество кодовых слов длины r в алфавите V численностью n=n(V) равно r-степени числа n:
(5) 
.
Слово образуется за r действий: 1) выбрать из алфавита букву на 1-е место в слове, 2) выбрать букву на 2-е место и т. д. Каждое действие независимо от варианта исполнения предыдущих действий выполняется n способами — всякий раз выбирается одна из n букв. Тогда по правилу умножения количество различных слов равно
.
#. Найдем количество кодовых слов в алфавите VB= {0; 1} длиной r= 8 символов. Это количество равно 
.
Кодовые слова данного типа называются, как известно, байтами.
Численность булеана
Теорема. Численность булеана 
множества X равна двойке, возведенной в степень, равную численности множества X:
(6) 
.
Каждое подмножество можно выразить индексным кодом — кодовым словом длины n (X), в котором k -й символ является индексом вхождения элемента xk в данное подмножество. Индекс 1, если xk принадлежит подмножеству; индекс 0, если нет. Так коду 000…0 соответствует пустое подмножество, коду 01010…0 — подмножество 
.
Очевидно взаимно однозначное соответствие подмножеств и индексных кодов, значит количество подмножеств равно количеству кодов длины n из алфавита {0; 1}. Таких кодов 
. Значит .
Перестановки
Df. Перестановками называются различные кортежи, составляемые из всех элементов множества.
Расположить предметы в ряд можно по-разному. Поменяв местами любые два предмета в «очереди», мы получим новую перестановку. Так из множества { a; b } можно получить перестановки {(a; b);(b; a)}; из множества {a; b; g} — множество перестановок
{(a; b; g), (a; g; b), (b; a; g), (b; g; a), (g; a; b), (g; b; a)}.
Количество различных перестановок зависит от числа переставляемых предметов. Количество перестановок n предметов обозначают Pn (читается: число перестановок n предметов).
Теорема. Число перестановок элементов множества равно факториалу его численности.
(7) 
Напомним, что факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n: n! = 1×2×3×…× n.
#. Составляется расписание уроков на понедельник в 8-а классе. Необходимо включить на этот день математику, литературу, географию, историю и физкультуру. Расписания суть перестановки этих пяти предметов. Число различных расписаний равно 
.
Опишем алгоритм образования перестановки:
| 1) | выбор элемента из множества V на первое место | n |
| 2) | выбор элемента из оставшихся на второе место | n –1 |
| 3) | выбор элемента из оставшихся на третье место | n –2 |
| ... | ... | ... |
| n) | выбор элемента последнего оставшегося на n -е место |
В правое поле записывается для каждого действия количество способов выполнения. На каждое место выбирается элемент из оставшихся после отбора на предшествующие места. Ясно, что число способов заполнения каждого места в перестановке на единицу меньше, чем предыдущего. Последнее место может быть занято только одним способом.
Число способов заполнения каждого места не зависит от вариантов выбора предшествующих элементов. Поэтому, к подсчету перестановок применимо правило умножения:
.
Записав произведение в обратном порядке, получим формулу (7).
Замечани е. Пустое множество считается упорядоченным: нуль элементов можно упорядочить одним способом. Чтобы распространить формулу (7) на пустое множество принято считать 0!=1.
Df. Перестановками с повторениями называются различные кортежи элементов множества, содержащего классы тожественных элементов.
К этому понятию приводит задача составления анаграмм — перестановок букв в слове или предложении. Очевидно, что количество анаграмм слова «молоко» меньше P 6. В самом деле: поменяв местами две буквы «о», мы не получим новую анаграмму. Обозначим неизвестное пока число анаграмм этого слова 
(шесть букв, из которых три повторяются). Пронумеруем теперь буквы «о» о1, о2, о3, чтобы они различались хотя бы номером. Переставляя в каждой анаграмме эти буквы, мы получим 
обычных перестановок шести элементов. Отсюда видно, что 
.
Можно сформулировать теорему о числе перестановок с повторениями.
Теорема. Число перестановок элементов множества с повторениями равно факториалу его численности, деленному на числа перестановок элементов в каждом классе.
(8) 
.
Df. Циклической перестановкой называется упорядоченное расположение элементов в замкнутую цепь (по кругу).
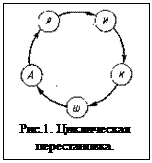
# Пять девочек танцуют в хороводе (см. рис. 1.).
В циклической перестановке определён порядок следования элементов, но неизвестен первый элемент. Так, если Аня и Катя поменяются местами, получается новая циклическая перестановка. Однако когда все девочки делают шаг в сторону, и каждая занимает место предшествующей девочки, новой циклической перестановки не образуется. Порядок следования девочек не изменяется.
Теорема. Число циклических перестановок элементов множества равно факториалу числа элементов без одного.
(9) 
Цепь из n звеньев можно разорвать n способами и получить n различных кортежей из каждой циклической перестановки (в этом можно убедиться на примере, показанном на рисунке 1 для n= 5). Следовательно, численности циклических и обычных перестановок связаны соотношением: 
. Отсюда получаем формулу (9).
Выборки без повторений (подмножества)
Df. Сочетаниями называются различные подмножества заданной численности некоторого исходного множества. Численность выбираемого подмножества r называется размером (или объемом) выборки.
# Пусть множество 
. Образуем из него различные подмножества выбирая по два элемента. Получим множество сочетаний
.
Пусть V — первичное множество, содержащее n=n (V) элементов, а r — численность каждого из образуемых подмножеств. Число r будем называть размером выборки. Очевидно, что r — целое число: 0£ r £ n.
Количество сочетаний обозначают 
(читают «цэ из эн по эр»)[1].
Теорема. Число сочетаний равно факториалу численности множества, деленному факториал размера одной выборки и на факториал размера ее дополнения.
(10) 
.
Для упрощения рассуждений используем множество V = {1; 2; …; n } в качестве первичного. Каждое сочетание взаимно однозначно можно зашифровать двоичным индексным кодом длиной n символов (см. доказательство теоремы о численности булеана). Например: код 11100…0 соответствует сочетанию {1; 2; 3}, код 10110…0 — {1; 3; 4}.
Количество сочетаний равно количеству соответствующих кодов.
Все используемые коды содержат r единиц и n–r нулей, а количество таких кодов равно искомому числу сочетаний. Данные коды различаются только последовательностью единиц и нулей. Значит, они могут быть сосчитаны как перестановки с повторениями. Тогда
.
Пример. Назначение трех дежурных из 24 учащихся класса.
Пусть учитель назначил Иванова, Петрова и Сидорова. Переставляя эти три фамилии, мы получим шесть различных размещений. Однако в данной задаче нам безразлично, в каком порядке дежурные перечислены. В любом из этих вариантов дежурят те же трое.
Обозначим количество сочетаний из n элементов по k символом 
. Из примера видно, что каждой неупорядоченной выборке k элементов отвечает Pk различныхразмещений:
.
Отсюда искомое число сочетаний равно
. (7)
В приведенном примере дежурных можно назначить
способами.
Df. Размещениями называют упорядоченные подмножества, содержащие заданное число r элементов некоторого первичного множества.
Очевидно, что размер выборки r — целое число, не превосходящее численность первичного множества n: 0£ r £ n. Количество размещений обозначают 
(читают «а из эн по эр»)[2].
# Пусть множество 
. Образуем из него различные упорядоченные выборки по два элемента. Получим множество размещений
.
Теорема. Число размещений равно факториалу численности множества, деленному на факториал числа элементов, не включенных в выборку.
(11) 
.
Размещение образуется в два действия:
| 1) | образуется подмножество (выборка) размера r |
|
| 2) | упорядочиваются элементы выборки | 
|
В правом поле записано число способов выполнения каждого действия. По правилу умножения:
.
Пример. Сколько трехбуквенных слов можно составить из 26 различных карточек разрезной азбуки? Заметим, что в математике под словом понимается любая цепочка символов, необязательно осмысленная.
Нетрудно видеть, что образуемые слова суть размещения. В самом деле: эти слова являются упорядоченными выборками, а буквы (карточки) в слове не повторяются. Искомое число трехбуквенных слов равно:
26×25×24=15600.
ВЫБОРКИ С ПОВТОРЕНИЯМИ
К выборкам с повторениями можно прийти, выбирая r элементов из генеральной совокупности, содержащей n классов, при достижении соглашения считать элементы внутри класса неразличимыми. Предполагается, что каждый класс содержит не менее r элементов.
Df. Сочетаниями с повторениями называются выборки заданного числа элементов из некоторого множества, в которых допускаются повторения элементов.
#. Выбор четырёх открыток, если в продаже имеются открытки пяти видов. Здесь возможен выбор нескольких одинаковых открыток.
Теорема. Число сочетаний с повторениями из n элементов по r элементов равно числу сочетаний без повторений по столько же элементов из n+r –1 элементов.
(12) 
.
#. Найдем количество различных покупок по четыре открытки, если в продаже имеются открытки 5 видов. Это количество равно
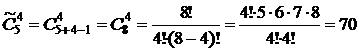
Размещения с повторениями можно определить по аналогии с сочетаниями с повторениями. Видно, что данному определению удовлетворяют рассмотренные ранее кодовые слова заданной длины (в них буквы могут повторяться). Алфавитом может служить любое множество, если всякий раз выбираемый элемент копируется в выборку, затем возвращается в первичное множество. Численность размещений с повторениями, как мы это уже установили, равна
(13) .
Размещениями с повторениями являются также упорядоченные выборки заданного размера из генеральной совокупности, содержащей n классов, при достижении соглашения считать элементы внутри класса неразличимыми. Предполагается, что каждый класс содержит не менее r элементов.
Пример. Располагая латинским алфавитом VL, можно составить 263=17576 различных трехбуквенных слов (предполагается n (VL)=26, k= 3).
Задания:
Законспектировать определения и формулы соединений в тетрадь.
Разобраться с таблицей и привести свой пример на каждый вид соединений.
Решить задачи:
1. Сколькими способами можно надеть по одному кольцу на 4 пальца руки, выбирая из 5 различных колец?
2. Научное общество состоит из 25 человек. Нужно выбрать президента, вице-президента, секретаря и казначея. Сколькими способами можно осуществить выбор, если каждый член общества может занимать не более одной выборной должности?
3. Из 9 солдат старшина произвольно отбирает двух для дежурства. Одного из них он назначает старшим. Сколькими способами он может это сделать?
4. Подсчитайте число возможных анаграмм (перестановок букв) из слова:
а) ананас; б) Миссисипи.
5. Сколько существует способов рассадить 7 человек на семи стульях?
6. Сколькими способами 9 человек могут встать в очередь в театральную кассу?
7. Сколько существует способов выбрать троих ребят из семерых желающих дежурить в столовой?
8. Из лаборатории, в которой работают 10 сотрудников, надо отправить четверых в командировку. Сколькими способами это можно сделать?
9. Сколько различных трехзначных чисел можно записать из цифр 1и 2?
10. В буфете имеется 4 вида пирожных. Сколькими способами можно купить 6 пирожных?
[1] От франц. combination — сочетание.
[2] От франц. arrangement — размещение.