Реализация лестничного фильтра

Методы реализации низкочастотной эквивалентной схемы из элементов и неоднородностей линий передачи могут быть самыми разнообразными. Например, в качестве индуктивного элемента можно использовать индуктивную диафрагму, а можно и индуктивный штырь. Индуктивное входное сопротивление имеет также короткозамкнутый отрезок линии короче четверти длины волны. Емкостные элементы в фильтре реализуются в виде емкостных диафрагм, емкостных штырей, короткозамкнутых отрезков линий короче полуволны, но длиннее четверти длины волны, и др.

Выбор той или иной конструкции элемента в фильтре зависит от множества разнообразных факторов, основными из которых являются: простота конструкции фильтра, малые потери в его элементах, простота настройки фильтра и др.

Ограничимся рассмотрением одного достаточно широко применяемого на практике варианта фильтра: полосового фильтра, выполненного из отрезков прямоугольного волновода. Эквивалентная схема такого фильтра изображена на рис. 20.2.1 в. Основным элементом полосового фильтра, выполненного из отрезков прямоугольных волноводов, является проходной резонатор, эквивалентный параллельному контуру, включенному в линию параллельно.

В качестве последовательного контура, включенного в линию последовательно, также используется проходной резонатор, ко входу и выходу которого подключены отрезки линии, имеющие длину в четверть волны на центральной частоте полосы пропускания фильтра (рис. 20.3.1). Действительно, нормированное входное сопротивление четвертьволнового отрезка, нагруженного на сопротивление 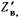равно 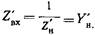(20.3.1)

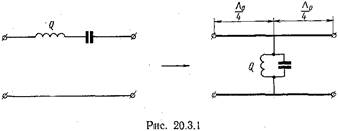
Нагрузкой четвертьволнового отрезка в данном случае является параллельный контур, нормированная входная проводимость которого, как известно, равна 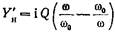(20.3.2) где 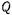- нагруженная добротность контура.

Нормированное входное сопротивление последовательного контура описывается выражением 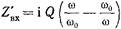(20.3.3)

Сравнивая равенства (20.3.2) и (20.3.3), убеждаемся в их полной тождественности. Следовательно, проходной резонатор, ко входу и выходу которого подключены четвертьволновые отрезки линии, эквивалентен последовательному контуру, включенному в линию последовательно. Отметим, что равенство (20.3.1) выполняется только при длине трансформирующего отрезка линии, равной четверти волны, т. е. на одной определенной частоте. Однако, как уже отмечалось в разд. 20.2, синтез фильтра по низкочастотной эквивалентной схеме вообще применим лишь для относительно узкополосных фильтров. Поэтому в первом приближении изменением электрической длины четвертьволнового отрезка можно пренебречь.

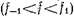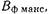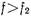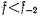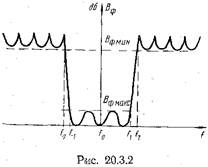
Коэффициент передачи и (соответственно величина вносимого фильтром затухания зависят от числа резонаторов и их нагруженной добротности. При расчете полосового фильтра число резонаторов и их нагруженные добротности определяются из условия, чтобы затухание в полосе пропускания фильтра не превышало заданной величины а в полосе заграждения ( и ) было не меньше заданной величины 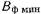(рис. 20.3.2). Иногда предъявляются требования к линейности фазовой характеристики фильтра в полосе пропускания. Удовлетворить указанным требованиям можно различными способами.

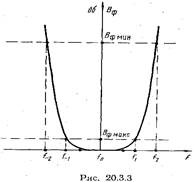
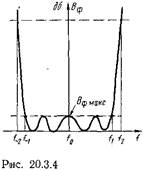
В технике сверхвысоких частот наибольшее распространение получили два вида полосовых фильтров: фильтры с максимально плоской характеристикой, у которых потери возрастают монотонно по мере отклонения частоты от средней частоты 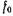полосы пропускания (рис. 20.3.3), и фильтры с чебышевской характеристикой, у которых зависимость величины потерь от частоты в полосе пропускания носит осциллирующий характер (рис. 20.3.4). Аналогичные характеристики уже рассматривались в предыдущей главе. Так же, как и в случае ступенчатого перехода, фильтр с чебышевской характеристикой содержит меньшее число элементов, чем фильтр с максимально плоской характеристикой при тех же электрических параметрах.

Уменьшение числа элементов в фильтре c чебышевской характеристикой, по существу, является следствием отказа от монотонного изменения функции 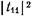и перехода к колебательному характеру изменения 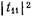в полосе пропускания фильтра. Дальнейшее уменьшение числа элементов может быть достигнуто путем отказа от монотонного увеличения затухания в полосе заграждения и перехода к колебательному как в полосе пропускания, так и в полосе заграждения (рис. 20.3.2). Однако, как показывает анализ, уменьшение числа элементов в фильтре с такой характеристикой по сравнению с чебышевским фильтром получается весьма небольшим, в то время как синтез и практическая реализация фильтра с подобной характеристикой существенно усложняются. Величина затухания, вносимого фильтром с максимально плоской характеристикой, описывается выражением: 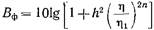(20.3.4) где , ,

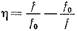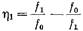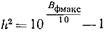
Число резонаторов определяется из равенства 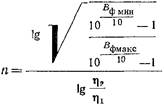(20.3.5) где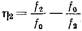

B случае фильтра с чебышевской характеристикой: 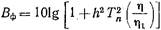(20.3.6) 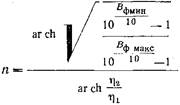(20.3.7) где 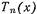-полином Чебышева первого рода n-го порядка.

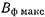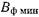Отметим, что в ф-лах (20.3.5) и (20.3.7) и - величины затухания в децибелах.

Необходимые нагруженные добротности резонаторов в фильтре с максимально плоской характеристикой определяются из равенства 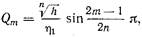(20.3.8) где m -порядковый номер резонатора (m= l, 2, 3, n). Формулы для расчета нагруженной добротности (фильтра с чебышевской характеристикой существенно сложнее. В настоящее время опубликованы обширные таблицы, из которых можно определить величины 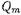при различных значениях пик.

Как следует из выражения (18.7.1-5), нагруженные добротности проходных резонаторов в фильтре определяются величиной модуля коэффициента отражения 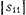от неоднородностей, включенных на входе и выходе резонатора. Находим величину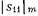 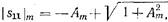(20.3.9) где 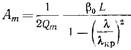(20.3.10)

Чем выше необходимая нагруженная добротность 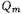резонатора, тем ближе согласно (20,3.9) величина 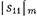к единице. При расчете модуля коэффициента отражения обычно пренебрегают тем, что длина резонатора L на резонансной частоте несколько отличается от полуволновой. Поэтому в (20,3.10) можно положить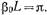

Требуемые значения коэффициента отражения могут быть реализованы с помощью различных неоднородностей: диафрагм, штырей и др. B волноводных фильтрах чаще всего применяют резонаторы, на входе и выходе которых включены решетки из индуктивных штырей (см. рис.. 18.7.4). Диаметр штырей в решетке можно определить либо по экспериментально снятым зависимостям величины 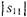от числа штырей и их диаметра, либо используя результаты теоретического анализа. При величине нагруженной добротности резонатора до 25-35 решетку целесообразно выполнить из двух штырей. В резонаторах с нагруженной добротностью от 40 до 80 решетка обычно выполняется из трех стержней. При более высоких добротностях число стержней в решетках соответственно увеличивается.

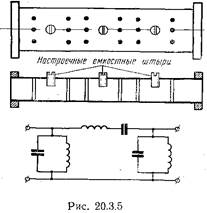
Общий вид трехзвенного волноводного полосового фильтра с четвертьволновыми отрезками и его эквивалентная схема показаны на рис. 20.3.6. Фильтр выполняется в виде отрезка волновода, в котором на определенных расстояниях друг от друга впаиваются решетки из индуктивных штырей. Внутренняя поверхность волновода часто покрывается тонким слоем серебра. Из-за неизбежных ори изготовлении (погрешностей резонансные частоты резонаторов в фильтре могут отличаться от требуемой. Поэтому для настройки в каждый резонатор вводится настроечный емкостный штырь, ввинчиваемый через широкую стенку волновода (рис. 20.3.5). Особое внимание при изготовлении резонаторов следует обращать на идентичность решеток из штырей на входе и выходе резонатора. Даже небольшое различие в коэффициентах отражения от каждой из решеток (Приводит к тому, что коэффициент передачи проходного резонатора на резонансной частоте становится меньше единицы. Это может привести к существенному увеличению потерь в фильтре. Радиусы штырей в обеих решетках должны отличаться не более чем на 2-3%, а расстояния между штырями в решетках должны выдерживаться с точностью до 0,4%. При тщательном изготовлении фильтра расхождение между экспериментальными и расчетными данными оказывается весьма незначительным.

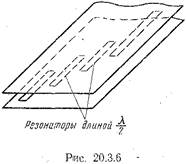
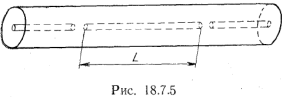
В коаксиальных и полосковых линиях в качестве проходного резонатора используется резонатор, изображенный на рис. 18.7.5. Нагруженная добротность подобного резонатора зависит от (величины зазора между отрезками внутренних проводников линий. Чем меньше этот зазор, тем больше торцевая емкость между проводниками и тем сильнее связь линии с резонатором, т. е. с уменьшением зазора нагруженная добротность падает. Так как площадь торцевой поверхности мала, то часто для получения (необходимой емкости требуются весьма малые зазоры. Но при этом существенно усложняется процесс производства и настройки фильтра, поскольку при малом зазоре даже небольшие погрешности в его величине сильно влияют на торцевую емкость, а следовательно, и на нагруженную добротность резонатора. Поэтому чаще применяют полосковые фильтры, в которых проходные резонаторы расположены параллельно друг другу и основной линии (рис. 20.3.6).

На рис. 20.3.6 не показаны диэлектрические (пластины, поддерживающие внутренние полоски. Область связи в таких конструкциях существенно длиннее, что позволяет оставлять достаточно большой зазор между проводниками.

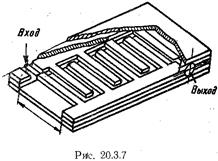
(В фильтре, изображенном на рис. 20.3.6, (резонаторами являются разомкнутые на обоих концах полуволновые отрезки линии. В фильтре на встречных штырях, изображенном на рис. 20.3.7, применены резонаторы, нагруженные на одном конце на емкость и замкнутые накоротко на другом конце. Как было показано в гл. 18, длина таких резонаторов зависит от величины торцевой емкости и не превышает четверти длины волны.

В качестве основного элемента волноводных режекторных фильтров широко применяют объемный резонатор, подключенный к основному волноводу, как показано на рис. 20.3.8а. Из рисунка видно, что (в резонаторе (параллельно индуктивной стержневой диафрагме включен коротко замкнутый отрезок линии длиной .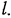

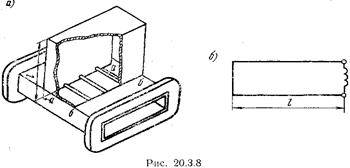
Эквивалентная схема резонатора имеет вид, изображенный «а рис. 20.3.86. Резонанс имеет место, когда входное сопротивление короткозамкнутого отрезка линии противоположно по знаку и равно по величине реактивному сопротивлению индуктивной диафрагмы. Поэтому короткозамкнутый отрезок должен обладать емкостным входным сопротивлением и (соответственно его длина больше четверти, но меньше (полуволны в волноводе. Если на входе резонатора включено емкостное реактивное сопротивление (например, емкостная диафрагма), длина короткозамкнутого отрезка не превышает четверти волны в волноводе.

На резонансной частоте, если пренебречь потерями (в резонаторе, входное сопротивление резонатора как параллельного контура равно бесконечности, что соответствует разрыву цепи между сечениями аа и бб основного волновода (рис. 20.3.8а).

В результате происходит практически полное отражение энергии. Путем включения подобных резонаторов на расстоянии, равном - 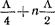'(n=0, 1, 2, 3,...), можно получить многозвенный режекторный фильтр, эквивалентная схема которого изображена на рис. 20.2.1г.