ФИЛЬТРЫ20.1. Классификация фильтров
Идеальным фильтром называется четырехполюсник, модуль коэффициента затухания которого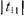 
равен единице в заданной полосе частот (полоса пропускания) и (бесконечно велик на всех частотах вне этой полосы (полоса заграждения). Напомним, что коэффициент затухания - величина, обратная коэффициенту передачи 
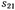четырехполюсника, и поэтому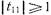 
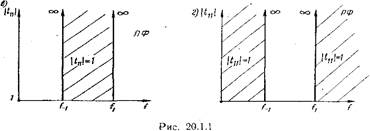
По взаимному расположению полос пропускания и заграждения фильтры делятся на фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ) и режекторные фильтры (РФ). Характеристики идеальных фильтров каждого типа приведены на рис. 20.1.1. Полосы пропускания на этих рисунках заштрихованы.
В полосе заграждения энергия электромагнитной волны либо отражается от входа фильтра (фильтр отражающего типа), либо поглощается в элементах фильтра (фильтр поглощающего типа).
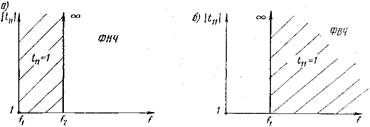
Реализация фильтров с идеально прямоугольными частотными характеристиками, изображенными на рис. 20.1.1, невозможна, поэтому частотные характеристики фильтров всегда имеют вид плавных кривых. В зависимости от выполнения фильтров форма этих кривых в большей или меньшей степени приближается к прямоугольной. Затухание фильтров обычно выражают в децибелах: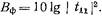 
(20.1.1). Полная величина потерь, вносимых фильтром, складывается из тепловых потерь и потерь, вызванных отражением от входа фильтра.
Эквивалентная схема фильтра отражающего типа
Фильтры отражающего типа состоят из реактивных элементов, сопротивление которых подбирается таким образом, чтобы на частотах полосы пропускания волны, отраженные от этих элементов, компенсировали друг друга на входе фильтра. Входное сопротивление фильтра в полосе пропускания близко к волновому сопротивлению линии. В пределах полосы заграждения компенсация отсутствует. Ослабление сигнала на выходе фильтра определяется почти полным отражением энергии от входа фильтра. Входное сопротивление фильтра в полосе заграждения близко к чисто реактивному.
Широкое применение в технике сверхвысоких частот получили так называемые лестничные отражающие фильтры. Эквивалентная схема таких фильтров совпадает со схемой лестничных фильтров, выполненных из реактивных элементов с сосредоточенными постоянными (рис. 20.2.1). Для реализации лестничных фильтров необходимы элементы линий передачи, эквивалентные по своим параметрам сосредоточенным индуктивностям, емкостям, последовательным и параллельным контурам. Элементом, соответствующим параллельному контуру, может служить проходной резонатор. Элементами, соответствующими сосредоточенным индуктивностям и емкостям, являются диафрагмы, штыри (см. разд. 17.2 и 17.3) и др. В связи с этим синтез лестничного фильтра сводится к решению двух задач:
- синтезу низкочастотной эквивалентной схемы фильтра, обладающей требуемыми характеристиками;
- реализации полученной эквивалентной схемы, т. е. замене сосредоточенных индуктивностей и емкостей эквивалентной схемы отрезками линий передачи, резонаторами, штырями, диафрагмами и другими неоднородностями.
Синтез фильтров по низкочастотной эквивалентной схеме дает хорошие результаты только для сравнительно узкополосных систем, так как близкая аналогия между неоднородностями и эквивалентными схемами из сосредоточенных постоянных сохраняется в относительно узкой полосе частот.
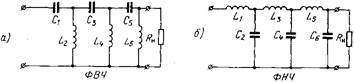
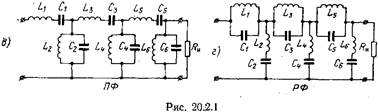
Методы синтеза низкочастотной эквивалентной схемы по заданным характеристикам фильтра подробно рассматриваются в курсе теории цепей. Поэтому ниже основное внимание обращено на реализацию эквивалентной схемы.