Решить систему уравнений 
.
I. Обозначив матрицу коэффициентов при неизвестных через 
, правую часть системы 
, а вектор неизвестных 
, эту систему уравнений можно записать в матричном виде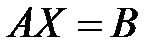 
. Это уравнение имеет единственное решение, если матрица 
– невырожденная, т.е. если ее определитель 
отличен от нуля. Тогда решение матричного уравнения запишется в виде 
, где 
– матрица, обратная к .
Вычислим 
по правилу треугольников:
или разложением по 2-й строке:
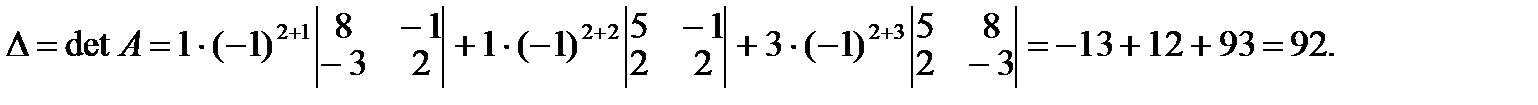
– невырожденная, и система имеет единственное решение. Найдем его.
1. Метод Гаусса.
Матрица системы уравнений 
. Запишем и приведем расширенную матрицу системы к диагональному виду с помощью эквивалентных преобразований:
~ 
~
(переставили для удобства первую и вторую строки матрицы). Теперь первую строку полученной матрицы последовательно умножим на (-5) и на (-2) и прибавим соответственно ко второй и третьей строкам:
~ 
~
далее умножим элементы 2ой строки на 5, а 3ей – на 3, затем вторую строку прибавим к третьей строке:
~ 
~ 
~
Теперь в полученной матрице разделим вторую строку на 15, а третью – на (-92). Получим матрицу, эквивалентную исходной:
~ 
Теперь можно получить решение системы. Третья строка матрицы равносильна уравнению 
. Вторая строка этой расширенной матрицы соответствует уравнению 
т.е.
Первая строка соответствует уравнению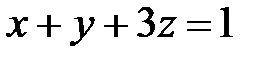 
, т.е.
.
Получаем следующий ответ:
.
2. По правилу Крамера.
Если главный определитель системы из 
уравнений с 
неизвестными отличен от 0, то система имеет единственное решение, которое ищется по формулам:
.
Посчитаем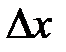 
, 
и 
. Каждый из них получается из главного определителя 
системы заменой столбца коэффициентов при неизвестном 
столбцом свободных членов уравнений, стоящих в правой части системы:
|
|
,
,
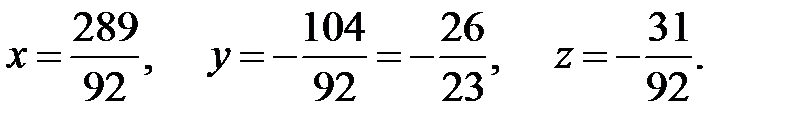
3. Решим систему матричным способом.
Решением матричного уравнения 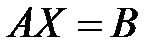находится как , где – обратная к матрица. Найдем её.
,
где 
– алгебраическое дополнение элемента 
матрицы .
 ,
|  ,
|  ,
|
 ,
|  ,
|  ,
|
 ,
|  ,
|  .
|
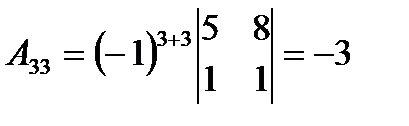Запишем обратную матрицу:
Теперь найдем X:
.
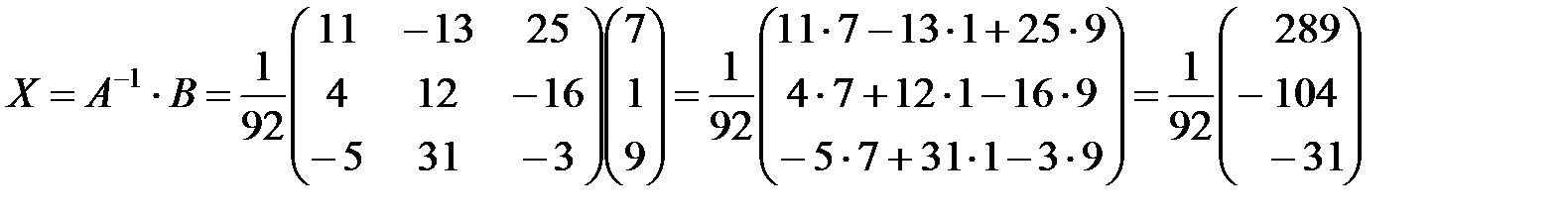Итак,
.
Таким образом, получили, что все три способа (метода) дали один и тот же ответ, т.е. задача решена верно.
Ответ: 
II. Разложим вектор 
по базису, составленному из векторов
, 
, 
.
Эти вектора образуют базис, т.к. определитель, составленный из них, есть 
из первой части задачи, а 
, 
эти вектора линейно независимы, 
они образуют базис.
Разложить вектор 
по векторам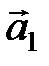 
, 
, 
значит представить его в виде линейной комбинации этих векторов, т.е.:
где 
– коэффициенты разложения, которые и нужно найти.
Это векторное уравнение в матричном виде запишется следующим образом:
, где
, 
,
и, чтобы найти 
, нужно найти 
: 
.
Заметим, что составленная из координат векторов матрица совпадает с матрицей заданной системы уравнений, а вектор 
есть вектор, стоящий в правой части системы. Эту систему мы уже решали, и 
находили. Таким образом, получим, что
.
Тем самым, разложение вектора 
по базису из векторов 
, , будет следующим:
.
II. МаТЕМАТИЧЕСКИЙ АНАЛИЗ
Задачи № 21-30
Вычислить передел последовательности.