
Для того чтобы определить в какой момент времени производительность максимальна исследуем функцию y (t), на экстремум. Найдём производную и приравняем её к нулю:
 при
при 
Так как при  , а при
, а при 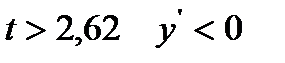 , то в точке
, то в точке 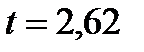 функция достигает максимума, т.е. производительность максимальна в момент времени
функция достигает максимума, т.е. производительность максимальна в момент времени 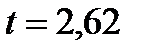 .
.
Производительность труда есть производная от функции объёма выпуска по времени. Следовательно, чтобы найти объём выпущенной продукции, нужно проинтегрировать y (t):
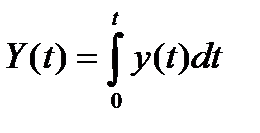 ,
,
 .
.
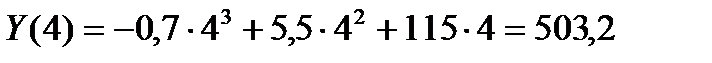 .
.
Объём выпущенной продукции за 4 часа составит 503,2.
Задачи № 61-70
Вычислить неопределённый интеграл
61. 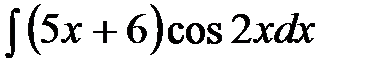
| 62. 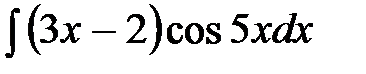
|
63. 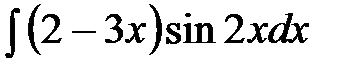
| 64. 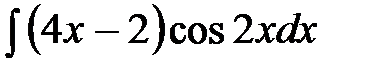
|
65. 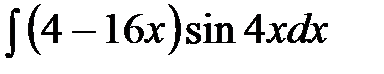
| 66. 
|
67. 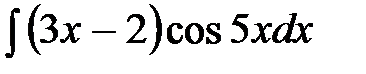
| 68. 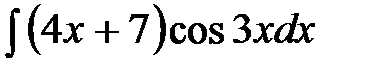
|
69. 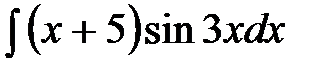
| 70. 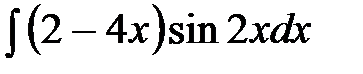
|
Пример решения задачи из заданий 61-70
Вычислить неопределённый интеграл 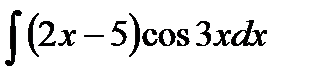 .
.
Воспользуемся формулой интегрирования по частям:
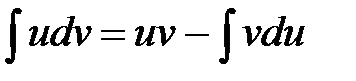
в качестве u возьмем u=2x - 5, а dv=cos3xdx. Тогда du=2dx, 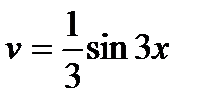 .
.
Получаем:

Задачи № 71-80
Найти общий интеграл дифференциального уравнения.
71.  72.
72. 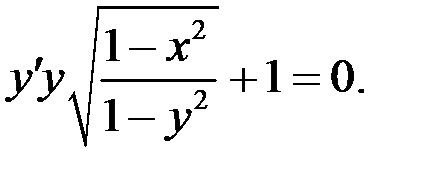
73. 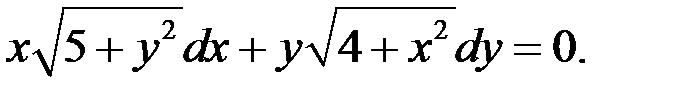 74.
74. 
75. 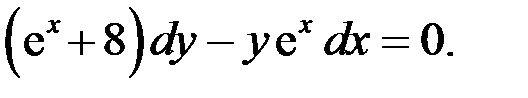 76.
76. 
77. 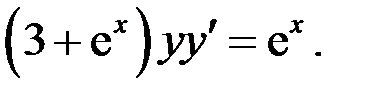 78.
78. 

79. 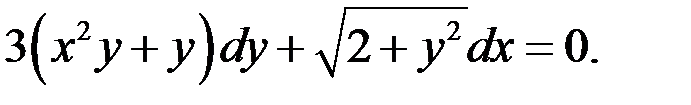 80.
80. 
Пример решения задачи из заданий 71-80
В некоторых ситуациях обыкновенные дифференциальные уравнения первого порядка легко решаются с помощью приема, который мы будем называть методом разделения переменных. Поясним суть приема на примере. Пусть дано уравнение:
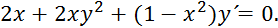
Постараемся преобразовать уравнение так, чтобы в левой его части было выражение, содержащее только переменную x, а в правой неизвестную функцию y.

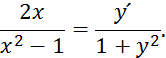
Если мы умножим формально обе части равенства на dx, то получим выражения, которые можно трактовать как дифференциалы некоторых функций, зависящих только от x и от y:

Равенство дифференциалов предполагает, что сами функции отличаются друг от друга на некоторую константу С, т.е.

Окончательно получаем 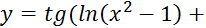 С.
С.
Задачи № 81-90
Найти область сходимости функционального ряда.
81. 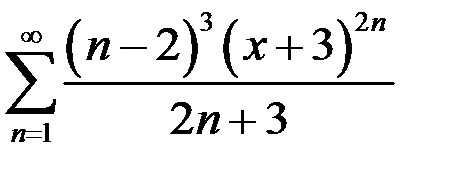 . 82.
. 82.  .
.
83. 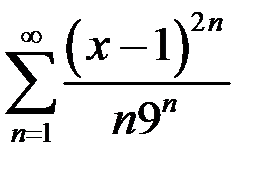 . 84.
. 84. 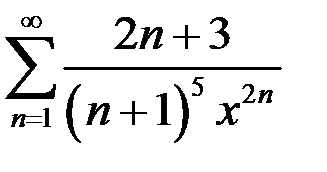 .
.
85.  . 86.
. 86.  .
.
87.  . 88.
. 88. 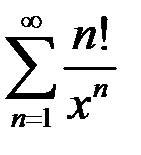 .
.
89.  . 90.
. 90. 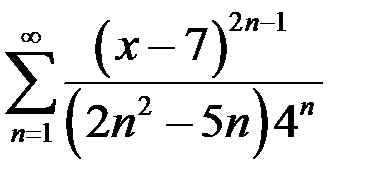 .
.
Пример решения задачи из заданий 81-90
Для решения задач этого раздела можно использовать признаки сходимости Даламбера или Коши. Согласно признаку Даламбера, для абсолютной сходимости ряда  достаточно, чтобы
достаточно, чтобы  .
.
Рассмотрим пример: пусть имеется функциональный ряд

Найдем предел дроби
 :
:
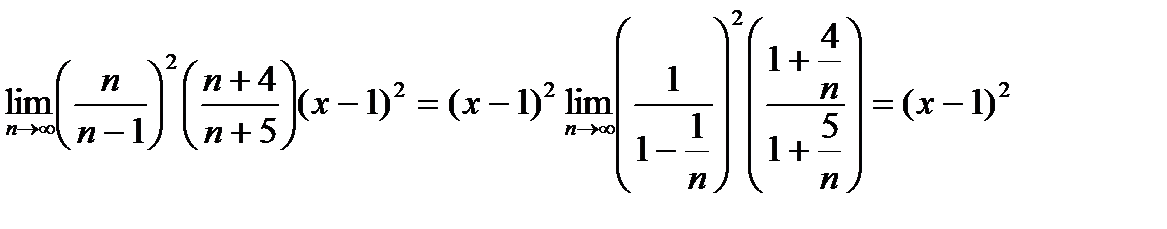 .
.
Если  , то ряд будет сходящимся. Откуда следует
, то ряд будет сходящимся. Откуда следует 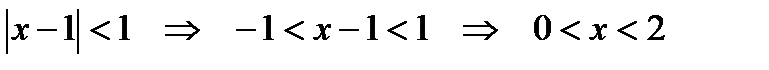 . Таким образом, область сходимости ряда включает интервал (0, 2). Проведем дополнительное исследование для случая, когда x = 0 или x = 2, т.е.
. Таким образом, область сходимости ряда включает интервал (0, 2). Проведем дополнительное исследование для случая, когда x = 0 или x = 2, т.е. 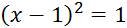 . В этих случаях получаем числовой ряд
. В этих случаях получаем числовой ряд
 .
.
Этот ряд, очевидно, расходится, т.к. не выполняется необходимый признак сходимости

Поэтому окончательный ответ – исходный ряд сходится для  .
.
III. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Задачи № 91-100
91. Имеются две одинаковые урны. В первой – семь белых шаров и три черных, а во второй – шесть белых и четыре черных. Наудачу выбирается урна и из нее наугад извлекается один шар.
а) Какова вероятность того, что шар оказался белым?
б) Шар оказался белым. Какова вероятность того, что его извлекли из 1-й урны?
92. В сборной по гимнастике 25% мастеров спорта, 42% кандидатов в мастера и 33% перворазрядников. Вероятность того, что мастер спорта или кандидат в мастера выполнит упражнения на «отлично», равна 0,92. Для перворазрядника эта вероятность равна 0,71.
а) Определить вероятность того, что член сборной, подошедший к снаряду, выполнит упражнение на «отлично».
б) Член сборной выполнил упражнение на «отлично». Какова вероятность того, что он преворазрядник?
93. Первый цех изготовил 45 лампочек, второй – 30, третий – 25. Вероятность того, что лампочка стандартная, для первого цеха равна 0,8, для второго – 0,7 и для третьего – 0,9. Из партии наугад взята одна лампочка.
а) Определить вероятность того, что она стандартная.
б) Лампочка оказалась стандартной. С какой вероятностью она изготовлена первым цехом?
94. В тире имеется три ружья, вероятности попадания из которых соответственно равны 0,6; 0,75; 0,8. Стреляющий берет наугад одно из ружей.
а) Определить вероятность попадания при одном выстреле?
б) Стреляющий попал по цели. С какой вероятностью он стрелял из 2-го ружья?
95. Приборы одного наименования изготавливаются двумя заводами. Первый завод поставляет 2/3 всех приборов, поступающих на производство, а второй – 1/3. Вероятность безотказной работы (надежность) прибора, изготовленного первым заводом, равна 0,95; второго – 0,85.
а) Определить надежность прибора, поступающего на производство.
б) Прибор, поступивший на производство, работает безотказно. С какой вероятностью он изготовлен первым заводом?
96. В первой коробке из 20 карандашей – 13 красных; во второй из 30 карандашей – 22 красных, а в третьей из 10 карандашей – 5 красных. Из наудачу выбранной коробки наудачу извлекают карандаш.
а) Найти вероятность того, что он красный.
б) Карандаш оказался красный. С какой вероятностью он принадлежал второй коробке?
97. В телеателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,85; 0,75; 0,9; 0,95.
а) Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок.
б) Взятый наудачу кинескоп выдержал гарантийный срок. С какой вероятностью это был четвёртый кинескоп?
98. В студенческой группе из 30 человек 20 занимаются лыжным спортом, 6 – легкой атлетикой и 4 – гимнастикой. Вероятность выполнить норму первого разряда такова: для лыжников – 0,85; для легкоатлетов – 0,9; для гимнастов – 0,75. Наудачу выбирают одного студента.
а) Найти вероятность того, что он выполнит норму первого разряда по своему виду спорта.
б) Студент выполнил норму. Какова вероятность того, что он гимнаст?
99. Для контроля за качеством продукции из трех партий деталей для проверки взята одна деталь. В одной партии 2/3 деталей бракованные, а в двух других – все детали стандартные.
а) Как велика вероятность обнаружить брак?
б) Деталь оказалась бракованной. С какой вероятностью она из первой партии?
100. В ящике содержится 13 деталей, изготовленных заводом №1, 19 деталей – заводом №2 и 18 – заводом №3. Вероятность того, что деталь отличного качества соответственно равна 0,8; 0,7; 0,9. Наудачу извлекают из ящика одну деталь.
а) Найти вероятность того, что отличного качества.
б) Деталь оказалась отличного качества. С какой вероятностью она принадлежит заводу №2?