Введение
В термодинамике для описания состояния систем, состоящих из большого числа атомов и молекул, используются макроскопические величины, например давление, температура, объем, внутренняя энергия и др. Эти понятия вводятся на основе физического эксперимента, он же является основой всех закономерностей, обуславливающих их связь между собой для конкретных макроскопических систем - газов, жидкостей или твердых тел.
Одна из важнейших задач теории и эксперимента - нахождение уравнения состояния вещества. В школьном курсе физики хорошо известно уравнение состояния идеального газа:
,(1)
связывающее его давление р и объем V с массой m, молярной массой М, абсолютной температурой Т и универсальной газовой постоянной R. Важно подчеркнуть, что это уравнение справедливо для газа, находящегося в состоянии термодинамического равновесия, когда давление и температура по всему объему одинаковы. Для смеси разных газов, содержащихся в некотором объеме, давление определяется суммой парциальных давлений газов - закон Дальтона. Этот закон выполняется при условии не только равенства температур газов, но и однородности смеси по всему объему. С известными ограничениями - не очень большая плотность, не очень низкие или высокие, по сравнению с «нормальными», температуры - уравнение состояния идеального газа используется для описания реальных газов, в том числе многоатомных. Часто оно же применяется и для типично неравновесных систем - таких, например, как земная атмосфера. Хотя в реальной атмосфере с высотой сложным образом изменяются давление, температура и химический состав газов, уравнение состояния достаточно точно описывает ее поведение на какой-то высоте или в небольшом объеме - например, в пределах одной комнаты.
Отметим, наконец, что уравнение состояния идеального газа используют для описания поведения паров, в том числе и насыщенных. При этом необходимо отчетливо понимать, чем ограничены возможности такого описания. Так, для насыщенного пара, если он таковым остается в течение всего процесса, давление определяется только температурой, причем для разных жидкостей величины давлений при одних и тех же температурах могут сильно отличаться. Однако с помощью уравнения состояния можно найти, например, массу пара в данном объеме, если известны давление и температура. Важное значение в термодинамике имеет понятие квазистатического, или обратимого процесса изменения состояния макроскопической системы. В ходе такого процесса состояние системы должно изменяться так медленно, чтобы каждое промежуточное состояние было равновесным. Обратимый процесс допускает возможность возвращения системы в первоначальное состояние через ту же последовательность промежуточных состояний, что и в прямом процессе.
Основным законом, описывающим обратимые процессы, является закон сохранения энергии - первое начало термодинамики:
Q = ∆U + A,(2)
Здесь Q - подведенное в процессе количество теплоты. ∆U - изменение внутренней энергии системы и А - работа системы против внешнего давления.
Внутренняя энергия системы - функция состояния, так что если начальное и конечное состояния системы равновесны, то изменение внутренней энергии не зависит от процесса перехода системы между ними. Для идеального газа внутренняя энергия зависит только от температуры:
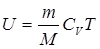.(3)
Коэффициент СV называют молярной теплоемкостью при постоянном объеме. Для одноатомного газа он равен ЗR/2, а для двухатомного 5R/2.
Работа и подведенное количество теплоты существенно зависят от способов перевода системы из начального состояния в конечное. Более того, изобразить процесс наглядно, например, в виде графика зависимости давления от объема системы, и вычислить работу по известным формулам возможно только для обратимых процессов.
Ввиду важности адиабатического процесса приведем вывод его уравнения для идеального газа.
Закон сохранения энергии в адиабатическом процессе, записанный для двух Близких состояний, отличающихся по температуре и объему на малые величины dTи dV, имеет вид
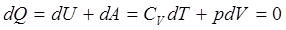(4)
Используя уравнение состояния для моля газа pV = RT, имеем:
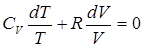(5)
Вспомним формулу для производной логарифмической функции:
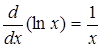(6)
и проинтегрируем наше равенство:
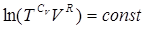(7)
Отсюда получаем
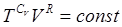(8)
или
(9)
Коэффициент γ = (СV + R)/CV называется показателем адиабаты. Для одноатомного газа γ = 5/3, а для двухатомного γ = 7/5.[1]
Обратимые и необратимые процессы
Обратимый процесс (то есть равновесный) - термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.
Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.
Обратимые процессы дают наибольшую работу. Большую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.
Следует отметить, что термодинамическая обратимость процесса отличается от химической обратимости. Химическая обратимость характеризует направление процесса, а термодинамическая - способ его проведения.
Понятия равновесного состояния и обратимого процесса играют большую роль в термодинамике. Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам.
Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, термодиффузия, теплопроводность, вязкое течение и др. Переход кинетической энергии макроскопического движения через трение в теплоту, то есть во внутреннюю энергию системы, является необратимым процессом.
Все происходящие в природе физические процессы делятся на два типа - обратимые и необратимые.
Пусть изолированная система в результате некоторого процесса переходит из состояния А в состояние В и затем возвращается в начальное состояние. Процесс называется обратимым, если возможно осуществить обратный переход из В в А через те же промежуточные состояния так, чтобы при этом не осталось никаких изменений в окружающих телах. Если такой обратный переход осуществить нельзя, если по окончании процесса в самой системе или окружающих телах остались какие-то изменения, то процесс является необратимым.
Любой процесс, сопровождаемый трением, является необратимым, ибо при трении часть работы всегда превращается в тепло, тепло рассеивается, в окружающих телах остается след процесса - нагревание, что делает процесс с участием трения необратимым. Идеальный механический процесс, происходящий в консервативной системе (без участия сил трения), был бы обратимым. Примером такого процесса является колебание тяжелого маятника на длинном подвесе. Из-за малого сопротивления среды амплитуда колебаний маятника практически не изменяется в течение продолжительного времени, при этом кинетическая энергия колеблющегося маятника полностью переходит в его потенциальную энергию и обратно.
Важнейшей принципиальной особенностью всех тепловых явлений, в которых участвует громадное число молекул, является их необратимый характер. Примером необратимого процесса является расширение газа, даже идеального, в пустоту. Предположим, что нам дан закрытый сосуд, разделенный на две равные части заслонкой (рисунок. 1). Пусть в части I находится некоторое количество газа, а в части II - вакуум. Опыт показывает, что если убрать заслонку, то газ равномерно распределится по всему объему сосуда (расширится в пустоту). Это явление происходит как бы "само собой" без внешнего вмешательства. Сколько бы мы не следили в дальнейшем за газом, он будет всегда оставаться распределенным с одинаковой плотностью по всему сосуду; сколько бы мы ни ждали, нам не удастся наблюдать того, чтобы газ, распределенный по всему сосуду I + II сам собой, то есть без вмешательства извне, ушел из части II и сконцентрировался весь в части I, что дало бы нам возможность вновь вдвинуть заслонку и тем самым возвратиться к исходному состоянию. Таким образом, очевидно, что процесс расширения газа в пустоту является необратимым.
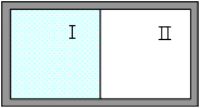
Рис 1. Закрытый сосуд, содержащий газ и вакуум и разделённый перегородкой[2]
Опыт показывает, что тепловые явления почти всегда обладают свойством необратимости. Так, например, если рядом находятся два тела, из которых одно теплее другого, то их температуры постепенно выравниваются, то есть тепло "само собой" перетекает от более теплого тела к более холодному. Однако обратный переход теплоты от более холодного тела к нагретому, который может быть осуществлен в холодильной машине, не идет "сам собой". Для осуществления такого процесса требуется затрата работы еще какого-либо тела, что приводит к изменению состояния этого тела. Следовательно, условия обратимости не выполняются.[2]
Кусочек сахара, помещенный в горячий чай, растворяется в нем, но никогда не бывает, чтобы из горячего чая, в котором уже растворен кусочек сахара, этот последний выделился и вновь собрался в виде кусочка. Конечно, получить сахар, выпарив его из раствора, можно. Но этот процесс сопровождается изменениями в окружающих телах, что свидетельствует о необратимости процесса растворения. Необратимым является и процесс диффузии. И вообще примеров необратимых процессов можно привести сколь угодно много. По сути, любой процесс, протекающий в природе в реальных условиях, является необратимым.
Итак, в природе существуют два вида принципиально различных процессов - обратимые и необратимые. М. Планк сказал однажды, что различие между обратимыми и необратимыми процессами лежит гораздо глубже, чем, например, между процессами механическими и электрическими, поэтому его с большим основанием, чем любой другой признак, следовало бы выбрать в качестве первейшего принципа при рассмотрении физических явлений.
Диссипативные системы
Диссипативные системы - динамические системы, у которых энергия упорядоченного процесса переходит в энергию неупорядоченного процесса, в конечном счёте - в тепловую. В механических диссипативных системах полная энергия (сумма кинетической и потенциальной) при движении непрерывно уменьшается (рассеивается), переходя в другие, немеханические формы энергии (например, в теплоту). Примеры диссипативных систем: твёрдые тела, между которыми действуют силы сухого или жидкостного трения, вязкая (или упруговязкая) среда, в которой напряжения зависят от скоростей деформаций, колебания электрического тока в системе контуров, затухающие при наличии омического сопротивления из-за перехода энергии в джоулеву теплоту, и т. д. Практически все системы, с которыми приходится реально сталкиваться в земных условиях, являются диссипативные системы. Рассматривать их как консервативные, т. е. как системы, в которых механическая энергия сохраняется, можно лишь в отдельных случаях, приближённо отвлекаясь от ряда реальных свойств системы. Диссипативные системы изучаются с макроскопической точки зрения термодинамикой неравновесных процессов, с микроскопической - статистической механикой неравновесных процессов или физической кинетикой.
Движение механических диссипативных систем исследуют с помощью обычных уравнений динамики для систем материальных точек, твёрдых тел или сплошных сред, включая в число действующих сил, так называемые диссипативные силы или силы сопротивления. Однако интегрирование получающихся уравнений бывает в большинстве случаев связано со значительными трудностями, особенно когда зависимость диссипативных сил от характеристик движения (например, от скоростей) не выражается в простой аналитической форме или когда точное решение задачи связано с необходимостью одновременно интегрировать уравнения движения среды и тела, движущегося в этой среде (задачи о движении тел в воде или воздухе, о пробивании брони и т.п.).
Изучение движения диссипативных систем значительно упрощается, когда скорости механических перемещений настолько малы, что диссипативные силы можно считать линейными функциями обобщённых скоростей. В этих случаях диссипация энергии может быть охарактеризована, так называемой, диссипативной функцией, численно равной половине полной механической энергии системы, рассеивающейся в единицу времени, и диссипативные силы могут быть просто выражены через эту функцию.[3]
Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем - несохранение объёма в фазовом пространстве, то есть невыполнение Теоремы Лиувилля.
Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, реакция Белоусова - Жаботинского и биологическая жизнь.
Термин «диссипативная структура» введен Ильёй Пригожиным.
Последние исследования в области «диссипативных структур» позволяют делать вывод о том, что процесс «самоорганизации» происходит гораздо быстрее при наличии в системе внешних и внутренних «шумов». Таким образом, шумовые эффекты приводят к ускорению процесса «самоорганизации».
Энтропия
Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы.
Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего количества тепла ∆Q к величине абсолютной температуры T:
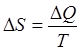(10)
Например, при температуре 0 °C, вода может находиться в жидком состоянии и при незначительном внешнем воздействии начинает быстро превращаться в лед, выделяя при этом некоторое количество теплоты. При этом температура вещества так и остается 0 °C. Изменяется состояние вещества, сопровождающееся выделением тепла, вследствие изменения структуры.
Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.
Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:
(11)
где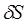 
- приращение (дифференциал) энтропии некоторой системы, а 
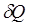- бесконечно малое количество теплоты, полученное этой системой.
Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).
Величина dS является полным дифференциалом, т.е. ее интегрирование по любому произвольно выбранному пути дает разность между значениями энтропии в начальном (А) и конечном (В) состояниях:
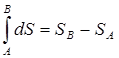(12)
Теплота не является функцией состояния, поэтому интеграл от δQ зависит от выбранного пути перехода между состояниями А и В. Энтропия измеряется в Дж/(моль·град).
Понятие энтропии как функции состояния системы постулируется вторым началом термодинамики, которое выражает через энтропию различие между необратимыми и обратимыми процессами. Для первых dS>δQ/T для вторых dS=δQ/T.
Поскольку энтропия является функцией состояния <https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D1%82%D0%B5%D1%80%D0%BC%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D1%81%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D1%8F>, в левой части равенства (11) стоит её полный дифференциал <https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BB%D0%BD%D1%8B%D0%B9_%D0%B4%D0%B8%D1%84%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB>. Напротив, количество теплоты является функцией процесса <https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D1%80%D0%BC%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%B2%D0%B5%D0%BB%D0%B8%D1%87%D0%B8%D0%BD%D1%8B>, в котором эта теплота была передана, поэтому 
считать полным дифференциалом нельзя.
Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики <https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D1%82%D1%8C%D0%B5_%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%BE_%D1%82%D0%B5%D1%80%D0%BC%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D0%BA%D0%B8> позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.
В силу второго начала термодинамики <https://ru.wikipedia.org/wiki/%D0%92%D1%82%D0%BE%D1%80%D0%BE%D0%B5_%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%BE_%D1%82%D0%B5%D1%80%D0%BC%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D0%BA%D0%B8>, энтропия Si замкнутой системы не может уменьшаться" (закон неубывания энтропии). Математически это можно записать так: dSi ≥0, индекс i обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла, как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла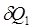 
при температуре T1 и уходит количество тепла 
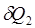при температуре T2. Приращение энтропии, связанное с данными тепловыми потоками, равно:
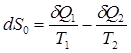(13)
В стационарных системах обычно 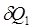= 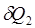, T1 > T2, так что 
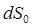< 0. Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется, таким образом, как "отрицательная энтропия".
Суммарное изменение энтропии открытой системы будет равно:
dS = dSi + dS0 (14)
Если всё время dS > 0, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если dS = 0, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру T1 внешнего потока тепла в температуру T2 уходящего из системы потока тепла.
В реальных экспериментах <https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D0%BF%D0%B5%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D1%82> очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии <https://ru.wikipedia.org/wiki/%D0%9A%D0%B0%D0%BB%D0%BE%D1%80%D0%B8%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F>.
Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость <https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BF%D0%BB%D0%BE%D1%91%D0%BC%D0%BA%D0%BE%D1%81%D1%82%D1%8C> при постоянных объёме и давлении (обозначенную CV и CP соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:
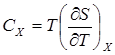,(15)
где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:
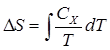(16)
Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P0,V0). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то
(17)
В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.
Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.[4]
Флуктуации и корреляции