Флуктуация (от лат. fluctuatio - колебание) - термин, характеризующий любое колебание или любое периодическое изменение. В квантовой механике - случайные отклонения от среднего значения физических величин, характеризующих систему из большого числа частиц; вызываются тепловым движением частиц или квантовомеханическими эффектами.
Примером термодинамических флуктуаций являются флуктуации плотности вещества в окрестностях критических точек, приводящих, в частности, к сильному рассеиванию света веществом и потере прозрачности (опалесценция).
Корреляция (от лат. correlatio - соотношение, взаимосвязь), корреляционная зависимость - статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Для таких величин, как энергия, объем и т. п., имеющих наряду с термодинамическим также и чисто механический смысл, понятие флуктуации само собой очевидно. Оно нуждается, однако, в уточнении для таких величин, как энтропия и температура, определение которых неизбежно связано с рассмотрением тела в течение конечных интервалов времени. Пусть, например, S(E,V) есть равновесная энтропия тела как функция его (средних) энергии и объема. Мы будем понимать под флуктуацией энтропии изменение функции S(E,V), рассматриваемой формально как функция от точных (флуктуирующих) значений энергии и объема.
Вероятность 
флуктуации пропорциональна 
, где Sn - полная энтропия замкнутой системы, т. е. всего тела в целом. С тем же успехом можно написать, что пропорциональна ~ exp ∆Sn, где ∆Sn - изменение энтропии при флуктуации.
Согласно формуле
(18)
имеем:
(19)
где 
- минимальная работа, необходимая для того, чтобы обратимым образом произвести заданное изменение термодинамических величин данной малой части тела (по отношению к которой остальные части тела играют роль среды). Таким образом,
(20)
Подставим сюда для Rmin выражение Rmin = ∆E - T0∆S + P0∆V, где ∆E, ∆S, ∆V - изменения энергии, энтропии и объема данной малой части тела при флуктуации, а T0 и P0 - температура и давление «среды», т. е. равновесные (средние) значения температуры и давления тела.
Таким образом, имеем
(21)
Заметим, что в таком виде эта формула применима к любым флуктуациям - как небольшим, так и значительным; под значительными здесь подразумеваются такие флуктуации, при которых, например, 
сравнимо с энергией самой малой части тела, но, конечно, по-прежнему мало по сравнению с энергией тела в целом. В применении к малым флуктуациям (какими они, вообще говоря, являются) формула (21) дает следующее. Разлагая в ряд, получим
(22)
Это выражение можно написать в виде
.(23)
Таким образом, получаем вероятность (21) флуктуации в виде
.(24)
Из этой общей формулы можно найти флуктуации различных термодинамических величин. Выберем сначала в качестве независимых переменных V и T. Тогда
(25)
Подставляя эти выражения в показатель формулы (24), найдем, что члены с ∆V ∆T сокращаются, и остается
.(26)
Это выражение распадается на два множителя, зависящих только от ∆T или ∆V. Другими словами, флуктуации температуры и объема статистически независимы, а потому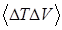 
= 0.
Сравнивая поочередно каждый из двух множителей, на которые распадается (26), с общей формулой
(27)
распределения Гаусса, найдем следующие выражения для средних квадратов флуктуации температуры и объема:
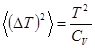,(28)
.(29)
Положительность этих величин обеспечивается термодинамическими неравенствами CV > 0 и 
.
Выберем теперь в качестве независимых переменных в (24) P и S. Тогда
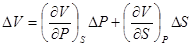, (30)
. (31)
Но согласно формуле dW = TdS + VdP имеем
, (32)
и поэтому
.(33)
Подставляя 
∆V и ∆T в (24), находим
.(34)
Как и (26) это выражение распадается на множители, зависящие соответственно от ∆V и ∆T. Другими словами, флуктуации энтропии и давления статистически независимы, и потому 
= 0.
Для средних квадратов флуктуации энтропии и давления находим
,(35)
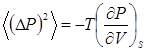.(36)
Из полученных формул видно, что средние квадраты флуктуации аддитивных термодинамических величин - объёма и энтропии-пропорциональны размерам (объему) тех частей тела, к которым они относятся. Соответственно средняя квадратичная флуктуация этих величин пропорциональна квадратному корню из объема, а относительная флуктуация - обратно пропорциональна этому корню. Для таких же величин, как температура и давление, обратно пропорциональны корню из объема уже сами их средние квадратичные флуктуации.
Формула (29) определяет флуктуацию объема некоторой части тела, содержащей определенное число N частиц. Деля обе стороны равенства на N2, находим флуктуацию объема, приходящегося на одну частицу:
(37)
Эта величина, очевидно, не может зависеть от того, рассматриваем ли мы флуктуацию в постоянном объеме или для постоянного числа частиц. Поэтому из последней формулы можно найти флуктуацию числа частиц, находящихся в определенном выделенном в теле объеме. Поскольку при этом V есть заданная величина, то надо положить
.(38)
Подставляя это в (37), находим
.(39)
Для некоторых вычислений удобно представить эту формулу в ином виде. Замечая, что производная 
подразумевается взятой при постоянном N, пишем
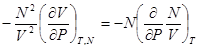.(40)
Но число частиц N как функция от P, T, V в силу соображений аддитивности должно иметь вид N = Vf(P,T); другими словами, N/V есть функция только от P и T, и потому безразлично, производится ли дифференцирование N/V при постоянном N или V,так что можно написать:
(41)
(мы воспользовались равенством 
). Таким образом, получаем следующую формулу для флуктуации числа частиц:
(42)
Наряду с рассмотренными термодинамическими величинами, тело характеризуется также импульсом P своего макроскопического движения относительно среды. В состоянии равновесия никакого макроскопического движения нет, т. е. P = 0. Движение, однако, может появиться в результате флуктуации; определим вероятность такой флуктуации. Минимальная работа Rmin в этом случае равна просто кинетической энергии тела
(43)
где M - его масса, ν = P/M - скорость макроскопического движения.
Таким образом, имеем для искомой вероятности
.(44)
Отметим, что флуктуации скорости статистически независимы от флуктуации других термодинамических величин. Средний квадрат флуктуации каждой из декартовых компонент скорости равен
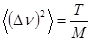(45)
он обратно пропорционален массе тела.
Из выведенных формул видно, что средние квадраты флуктуации таких величин, как энергия, объем, давление, скорость, обращаются при абсолютном нуле в нуль (пропорционально первой степени температуры). Это является общим свойством всех термодинамических величин, имеющих также и чисто механический смысл, но, вообще говоря, не относится к таким чисто термодинамическим величинам, как энтропия и температура.
Формула (28) для флуктуации температуры может быть истолкована еще и с другой точки зрения. Как мы знаем, понятие температуры может быть введено через посредство распределения Гиббса; при этом температура рассматривается как параметр, определяющий это распределение. В применении к изолированному телу распределение Гиббса полностью описывает его статистические свойства с той лишь неточностью, что оно дает весьма малые, но все же отличные от нуля флуктуации полной энергии тела, которых в действительности не должно быть. Напротив, если считать энергию величиной заданной, то нельзя приписывать телу вполне определенную температуру, и надо считать, что последняя испытывает флуктуации, определяющиеся формулой (28), в которой CV будет теплоемкостью тела в целом. Эта величина, очевидно, характеризует точность, с которой может быть дано определение температуры изолированного тела.[5]
Корреляция флуктуации
термодинамический диссипативный адиабатический флуктуация
Утверждение, что в однородном изотропном теле (газ или жидкость) все положения частиц в пространстве равновероятны, относится к каждой данной частице при условии, что все остальные частицы могут занимать произвольные положения. Это утверждение, конечно, не находится в противоречии с тем, что между взаимным расположением различных частиц должна существовать в силу их взаимодействия некоторая корреляция; последняя означает, что если рассматривать, скажем, одновременно две частицы, то при заданном положении первой частицы различные положения второй будут не равновероятными.
Для упрощения записи дальнейших формул мы ограничимся рассмотрением одноатомного вещества, у которого положение каждой частицы полностью определяется ее тремя координатами.
Обозначим посредством ndV вероятность частице находиться в элементе объема dV при условии, что одна частица находится в элементе dV. В силу бесконечной малости объема dV в нем может находиться одновременно не более одной частицы; вероятность нахождения в нем сразу двух частиц есть бесконечно малая величина более высокого порядка. Поэтому среднее число частиц ndV есть в то же время вероятность частице находиться в элементе dV.
Рассмотрим среднее значение
,(46)
где n1, n2 - значения плотности числа частиц n(r) в двух различных точках пространства, а посредством 
обозначено среднее значение плотности, одинаковое в силу однородности тела во всех, его точках (
). Если бы между положениями различных частиц никакой корреляции не было, то мы имели бы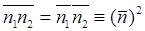 
и среднее значение (46) обратилось бы в нуль. Таким образом эта величина может служить мерой корреляции.
Обозначим посредством n12dV2 вероятность частице находиться в элементе объема dV2 при условии, что одна частица находится в элементе dV1; n12 есть функция абсолютной величины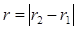 
относительного расстояния обоих элементов.
Поскольку, как уже было отмечено, число ndV есть 0 или 1, то очевидно, что среднее значение
(47)
В этом соотношении, справедливом при r1 ≠ r2, нельзя, однако, перейти к пределу r2 → r1, так как при выводе не учтено, что если точки 1 и 2 совпадают, то частица, находящаяся в dV1, тем самым находится и в dV2. Легко видеть, что соотношение, учитывающее это обстоятельство, имеет вид
.(48)
Действительно, выделим некоторый малый объем ∆V и, умножив (48) на в dV1dV2, проинтегрируем по этому объему. Член 
даст при этом малую величину второго порядка (пропорциональную (∆V)2); член же с δ-функцией даст ∆V, т. е. величину первого порядка. Мы получим, следовательно,
(49)
Как и должно быть, принимая во внимание, что с точностью, до величин первого порядка в малом объеме может находиться лишь 0 или 1 частица. Подставляя (48) в (46), найдем:
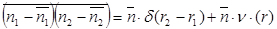,(50)
где мы ввели функцию
,(51)
которую будем называть Функцией корреляции. Ясно, что корреляция должна исчезать при неограниченном возрастании расстояния r, т. е.
n(¥) = 0.(52)
Выделим в рассматриваемом теле некоторый конечный объем V и, умножив равенство (49) на dV1dV2, проинтегрируем по dV1 и dV2. Имея в виду, что
(53)
где N - полное число частиц в объеме V (так что 
), найдем:
(54)
Переходя от интегрирования по dV1 и dV2 к интегрированию, скажем, по dV1 и по относительным координатам r = r2 - r1, (произведение дифференциалов которых обозначим dV) и имея в виду, что n зависит только от r, получим окончательно следующее выражение для интеграла от функции корреляции:
.(55)
Таким образом, интеграл от функции корреляции по некоторому объему связан со средним квадратом флуктуации полного числа частиц в этом объеме. Воспользовавшись для последнего термодинамической формулой
, (56)
можно выразить этот интеграл через термодинамические величины:
(57)
В обычном (классическом) идеальном газе получается:
(58)
как и должно быть. Ясно, что в идеальном газе, рассматриваемом с точки зрения классической механики, никакой корреляции между положениями различных частиц вообще нет, поскольку частицы идеального газа предполагаются невзаимодействующими друг с другом.
Напротив, в жидкости (при температурах, не близких к критической точке) первый член в выражении (57) мал по сравнению с единицей в силу малой сжимаемости жидкости. В этом случае можем написать:
(59)
Это значение интеграла от функции корреляции в некотором смысле соответствует взаимной непроницаемости частиц жидкости, рассматриваемых как плотно упакованные твердые шарики.
Далее, умножим равенство (50) с обеих сторон на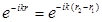 
и снова проинтегрируем по dV1 dV2. Мы получим:
(60)
или окончательно:
.(61)
Это соотношение определяет компоненты Фурье функции корреляции через средние квадраты компонент Фурье плотности n.[5]
Список литературы
1. Шеронов А., Обратимые и необратимые процессы в термодинамике.
Научно-популярный физико-математический журнал "Квант".
. Караваева В.В., Александров Н.А. Молекулярная физика. Учебное пособие. Томск, 2007. Электронный ресурс, режим доступа: https://ido.tsu.ru/schools/physmat/data/res/molek/uchpos/.
Осипов А.И. Термодинамика вчера, сегодня, завтра. Часть 2. Неравновесная термодинамика // Соросовский Образовательный Журнал. 1999. № 4. С. 79-85.
. Волькенштейн М. В. Энтропия и информация. - М.: Наука, 1986. - 192 с.)
. Fermi, E., Thermodynamics, Prentice Hall (1937). - Русский перевод: Ферми, Энрико, Термодинамика, Харьков: Изд-во Харьковского ун-та, 1969. - 140 с.