Точки устранимого разрыва.

Точки разрыва I рода.

Точки разрыва II рода.

ОПР3: Точка А – точка устранимого разрыва, если предел функции в этой точке существует, но функция в этой точке неопределена; либо предел функции в этой точке не равен значению функции в этой точке.

ОПР4: Точка А – точка разрыва I рода, если в этой точке функция имеет конечный правый предел, конечный левый предел, но они не равны между собой.

ОПР5: Точка А – точка разрыва II рода, если в этой точке функция не имеет по крайней мере одного из пределов (правого или левого) или хотя бы один из односторонних пределов бесконечен.

25. Теорема об устойчивости знака непрерывной функции.

ТЕОР1: Пусть функция f(x) задана на множестве Х непрерывна в точке Х0ÎХ и f(x)¹0. Тогда существует положительное число d такое, что для всех хÎ(Х0 - d, Х0+d)ÇХ функция имеет тот же знак, что и f(X0).

Док-во: Пусть f(X0)>0. Так как функция непрерывна, то для ("e>0) ($d>0) такое, что для ("хÎХ: |X0-x|<d) выполняется неравенство |f(x) – f(X0)|<e. Последнее неравенство в виде f(X0) - e<f(x)<f(X0)+e, оно выполняется для "хÎ(Х0 - d, Х0 + d). Возьмем e=f(X0)>0, тогда для "хÎ(Х0 - d, Х0 + d) f(x)>0.

Если f(X0)<0, то рассмотрим функцию –f(x). Тогда –f(X0)>0 и существует d - окрестность точки Х0, в которой –f(x)>0. Þ f(x)<0.

26. I теорема Больцано – Коши.

ТЕОР1: Пусть функция f(x) непрерывна на сегменте [A, B] и на концах сегмента имеет значения разных знаков. Тогда существует точка СÎ(А, В) в которой f(C)=0.

Док-во: Пусть f(A)<0 и f(B)>0. Разделим сегмент [A, B] пополам. Если значение функции в середине сегмента равно 0, то теорема доказана. В противном случае выберем тот из двух полученных сегментов, на концах которого функция имеет значение разных знаков. Обозначим его [A1, B1]. Повторим деление. Если продолжать этот процесс неограниченно, то либо на к-ом шаге значение функции в середине сегмента [Aк, Bк] окажется равным 0. Либо получим последовательность [A, B] É [A1, B1] É [A2, B2] É…É [An, Bn]… вложенных сегментов, причем Bn – An = (В – А)/ ®0 при n®¥ и на концах каждого сегмента [An, Bn] функция имеет значения разных знаков. Þ Существует точка С принадлежащая всем сегментам. Докажем, что f(C)=0.

ПП: Пусть f(C)>0, тогда существует окрестность точки С (по Т об устойчивости знака непрерыв Ф), в которой f(C)>0. В эту окрестность при большом n попадает сегмент [An, Bn]. Þ На [An, Bn] будет выполняться неравенство f(x)>0, это противоречит тому, что на концах [An, Bn] функция имеет значения разных знаков (если f(C)<0 аналогично).

27. II теорема Больцано – Коши.

ТЕОР: Пусть функция f(x) непрерывна на сегменте [a, b], причем f(a)=A, f(b)=B. Пусть далее С – любое число, заключенное между А и В. Тогда на сегменте [a, b] найдется точка X0 такая, что f(X0)=C.

Док-во: Пусть A<B и A<C<B. Рассмотрим функцию j(x) = f(x) – C. Эта функция непрерывна на [a, b] как разность непрерывных функций и принимает на концах сегмента значения разных знаков: j(a)=f(a) – C=A – C<0 и j(b)=f(b) – C=B – C>0. Тогда (по1 Т Б-К) существует точка Х0Î(a, b) такая, что j(Х0)=f(X0) – C=0Þ f(X0)=C.

28. I теорема Вейерштрасса.

ТЕОР: Если функция f(x) определена и непрерывна на сегменте [a, b], то она ограничена на этом сегменте.

Док-во:ПП: пусть f(x) не ограничена на [a, b]. Разделим сегмент пополам, тогда, по крайней мере, на одном из сегментов функция не ограничена. Обозначим этот сегмент [a1, b1]. Продолжим процесс деления неограниченно получим последовательность [a, b] É [a1, b1] É [a2, b2] É…É [an, bn]… Это последовательность вложенных отрезков, на каждом из них функция не ограничена (по предположению). По построению bn - an =(b – a)/ ®0 при n®¥. Тогда существует единственная точка С принадлежащая всем этим отрезкам. Функция f(x) определена и непрерывна на [a, b]. Þ Она непрерывна в точке С, но тогда (лемма) существует окрестность точки С, в которой f(x) ограничена. При большом n в эту окрестность попадает сегмент [an, bn], на котором функция также ограничена. Противоречие. Þ Она ограничена на этом сегменте.

ЗАМ: теорема неверна, если сегмент заменить на интервал.

29. II теорема Вейерштрасса.

ТЕОР: Если функция f(x) непрерывна на сегменте [a, b], то она достигает на этом сегменте своих точных граней, т. е. существуют точки X1, X2Î[a, b] такие, что f(X1)=M=sup f(X2)=m=inf f(x) на сегменте [a, b].

Док-во: Так как f(x) непрерывна на [a, b], то она ограничена на этом отрезке (1 Т В). Þ Существует точная верхняя М и точная нижняя m грани функции f(x) на отрезке [a, b]. Докажем, что функция достигает М, т. е. существует точка Х1Î[a, b], что f(X1)=M. Тогда для "хÎ[a, b] выполняется неравенство f(x)<M. Построим вспомогательную функцию F(x)= >0 для "хÎ[a, b]. Функция F(x) непрерывна (как частное непрерывных функций). Но тогда (по 1 Т В) F(x) ограничена, т. е. найдется число m>0 такое, что "хÎ[a, b] £m или f(x)£M – 1/m.. Т. о. число М – 1/m является верхней гранью f(x) на отрезке [a, b]. Но это противоречит тому, что М – точная верхняя грань f(x) на отрезке [a, b]. Þ Существует точка X1Î[a, b], в которой f(x)=M. (Нижняя грань аналогично)

ЗАМ: после доказательства факта, что непрерывная на [a, b] функция достигает своих точной нижней и верхней граней, точную верхнюю грань принято называть максимальным значением, а точную нижнюю грань – минимальным значением. Теорема формулируется:

Непрерывная на [a, b] функция принимает на нем свое min и max значение.

30. Теорема о непрерывной сложной функции.

ТЕОР: Пусть функции Z=j(x) непрерывна в точке X0, а функция Y=f(z) непрерывна в точке Z0. Тогда сложная функция Y=f(j(x)) непрерывна в точке X0.

Док-во: Пусть Х1, Х2, Х3,…, Хn,… - " последовательность из множества Х, сходится к точке Х0. Тогда в силу непрерывности функции Z=j(x) в точке Х0 имеем lim Zn = lim j(Xn) = j(X0) = Z0 при n®¥, то есть соответствующая последовательность точек Z1, Z2, Z3,…, Zn,… сходится к точке Z0. В силу непрерывности функции f(z) в точке Z0 имеем lim f(Zn) = f(Z0), т. е. lim f[j(Xn)] = f[j(X0)]. Получаем, что предел функции f(j(x)) в точке Х0 равен значению функции в точке Х0. Þ Функция непрерывна.

31. Теорема о непрерывной обратной функции.

ТЕОР: Пусть функция Y=f(x) определена, строго монотонна и непрерывна на некотором промежутке Х и пусть У – множество ее значений. Тогда на множестве У обратная функция X=j(y) однозначна, строго монотонна и непрерывна.

ЗАМ: если обратная функция X=j(y) однозначна, то, очевидно, что f – обратная функция для функции j, говорят, что f и j – взаимообратные.

 

32. Понятие производной.

ОПР1:Приращением функции Y=f(x) в точке X0, отвечающим приращению аргумента DX, будем называть число DY=f(X0+DX) – f(X0).

ОПР2:Производной функции Y=f(x) в данной точке X0 называется предел при DX®0 отношения приращения функции к приращению аргумента. При условии, что он существует – конечная производная. Если он равен бесконечности, то функция имеет бесконечную производную. Если функция имеет конечную производную в каждой точке множества Х, то можно рассматривать производную как функцию определенную на множестве Х.

33. Геометрический смысл производной.

Пусть функция Y=f(x) определена на интервале (a, b) и пусть точка А на графике функции соответствует значению аргумента Х0, а точка В – значению (Х0+DХ). Проведем через А и В прямую и назовем ее секущей. Обозначим через j(DХ) угол между секущей и осью ОХ.

ОПР1: Если при DХ®0 существует lim j(DX)= j 0, то прямую с угловым коэффициентом К=tg j 0, проходящим через точку А(Х0, f(X0)), называют предельным положением секущей АВ при DХ®0 (или В®А).

ОПР2: Касательной S к графику функции Y=f(x) в точке А будем называть предельное положение секущей АВ при DХ®0 (или при В®А).

ТЕОР1: Если функция Y=f(x) имеет в точке Х0 производную, то существует касательная к графику Y=f(x) в точке М(X0, f(X0)), угловой коэффициент касательной K=tg j 0 = f ’(X0).

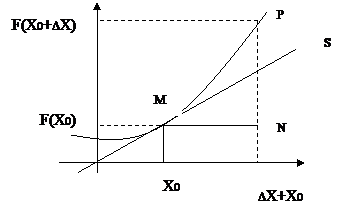Док-во: Проведем прямую MN || OX, тогда PN || OY, MN=DX, PN=DY, ÐPMN=j Þ tg j(DX) = DY/DX = Þ j(DX) =arctg DY/DX. Перейдем к пределу при DX®0. Так как существует производная f ’(X0), то существует и предел lim DY/DX=f ’(X0) и так как функция arctg DY/DX непрерывна Þ существует предел правой части равенства:

lim arctg DY/DX= arctg (lim DY/DX)=arctg f ’(X0). Þ Существует предел и левой части равенства. Получаем lim j(DX) = arctg f ’(X0). Þ Существует предельное положение секущей РМ, т. е. существует касательная к графику функции Y=f(x) в точке А(X0, f(X0)), причем угол наклона этой касательной к оси ОХ равен arctg f ’(X0) и, значит, угловой коэффициент касательной tg j 0= f ’(X0).

ОПР3: Составим уравнение касательной к графику функции Y=f(x) в точке A(X0, f(X0)). Уравнение прямой, проходящей через точку C(a, b) с угловым коэффициентом k имеет вид Y=b+k(x –a). Но в точке А значение функции равно f(X0), поэтому в уравнении а=Х0, b= f(X0), k= f ’(X0). Получаем уравнение касательной Y= f(X0)+ f ’(X0)(X - X0).

ОПР4:Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной в этой точке.

 

 

34. Понятие дифференцируемости функции.

ОПР1: Функция Y=f(x) называется дифференцируемой в точке X0, если ее приращение DY в этой точке можно представить в виде DY=A·DX+a(DX)·DX, где А – некоторое число, не зависящее от DX, а a(DX) – функция аргумента DX, являющаяся бесконечно малой при DX®0, т. е. lim a(DX)=0.

ТЕОР1: Для того, чтобы функция Y=f(x) была дифференцируема в точке X0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Док-во:Необходимость: Пусть функция Y=f(x) дифференцируема в точке X0, т. е. ее приращение представимо в виде DY=A·DX+a(DX)·DX. Поделим это равенство на DX, получим DY/DX=А+a(DX). Переходя к пределу при DX®0, имеем lim (DY/DX)=lim (А+a(DX))=A. Þ Производная в точке X0 существует и f ’(X0)=А.

Достаточность: Пусть существует конечная производная f ’(X0), т. е. lim (DY/DX)= f ’(X0). Обозначим f ’(X0)=А, тогда функция a(DX)=DY/DX - А является бесконечно малой при DX®0. Из последнего равенства имеем DY=A·DX+a(DX) ·DX, где lim a(DX)=0. Получено представление DY=A·DX+a(DX)·DX. Þ Функция Y=f(x) дифференцируема в точке X0.

35. Непрерывность и дифференцируемость функции.

ТЕОР2: Если функция Y=f(x) дифференцируема в данной точке X0, то она и непрерывна в этой точке.

Док-во: Так как функция Y=f(x) дифференцируема в точке X0, то ее приращение в этой точке можно представить в виде DY=A·DX+a(DX)·DX. Тогда, переходя к пределу при DX®0 получаем limDY=A·limDX+lim a(DX)·limDX=0, что означает непрерывность функции Y=f(x) в точке X0 согласно определению.

36. Понятие дифференциала. Геометрический смысл.

Пусть функция Y=f(x) дифференцируема в точке X0, т. е. ее приращение DY в этой точке представимо в виде: DY=A·DX+a(DX)·DX, где lim a(DX)=0. Слагаемое A·DX является при DX®0 бесконечно малой одного порядка с DX (при А¹0), оно линейно относительно DX. Слагаемое a(DX) при DX®0 бесконечно малая более высокого порядка, чем DX, так как lim (a(DX) ·DX)/DX = lim a(DX)=0. Т. о. первое слагаемое является главной частью приращения функции.

ОПР1:Дифференциалом функции Y=f(x) в точке X0 называется главная, линейная относительно DX, часть приращения функции в этой точке. Обозначается dY= A·DX.

Если А=0, то A·DX не является главной частью приращения DY. Однако и в этом случае по определению дифференциал функции в точке X0 равен A·DX, т. е. dY=0. Можно записать дифференциал в виде dY= f ’(X0) ·DX.

Дифференциалом независимой переменной называют приращение этой переменной dX=DX. Соотношение имеет вид dY= f ’(X0) ·dX. Можно вычислить f ’(X0): f ’(X0)=dY/dX.

Пусть точка М на графике соответствует значению аргумента X0, а точка Р – значению аргумента Х0+DХ. Проведем касательную MS к графику в точке М. Обозначим через a угол, образованный касательной с осью ОХ. Пусть MN || OX, PN || OY и Q – точка пересечения касательной с PN. Тогда приращение функции равно величине отрезка PN. Из треугольника MQN имеем: QN= tg a·DX= f ’(X0) ·DX= dY Þ Дифференциал функции равен величине отрезка QN. Видно, что PN и QN различны. Т. о. дифференциал dY функции f(x) в точке X0 равен приращению ординаты касательной MS к графику в точке М.

 

37. Правила дифференцирования суммы, разности, произведения, частного двух функций.

ТЕОР1: Если функции u=U(x), v=V(x) дифференцируемы в точке х, то сумма, разность, произведение и частное этих функций также дифференцируемы в этой точке и имеют место следующие формулы: (u±v)’=u’±v’; (u·v)’=u’·v+v’·u; ’= .

Док-во: Воспользуемся определением производной, равенством f(x+DX)=f(x)+ DY и теоремой о пределах суммы, разности, произведения и частного.

(u±v)’=lim [u(x+DX) ± v(x+DX)] – [u(x) ± v(x)] = lim u(x+DX) –u(x) ± v(x+DX) – v(x) =

DX DX DX

= lim u(x+DX) –u(x) ± lim v(x+DX) – v(x) = lim (Du /DX) ± lim (Dv /DX) = u’ ± v’

DX DX

(u·v)’= lim u(x+DX) ·v(x+DX) – u(x) ·v(x) = lim (u(x)+ Du) · (v(x)+Dv) - u(x) ·v(x) =

DX DX

lim u(x) ·v(x) + Du ·v(x) + Dv ·u(x) + Du ·Dv - u(x) ·v(x) =lim [v(x) ·(Du /DX) +u(x) ·(Dv /DX) +Dv·(Du/DX)]

DX

= v ·lim (Du /DX) + u ·lim (Dv /DX) + lim Dv · lim (Du/DX) = v · u’ + u · v’ + 0 · u’ = u’ · v+ u · v’

(u / v)’=lim [u(x) + Du] / [v(x)+Dv] – [u(x) / v(x)] =lim u(x+DX) · v(x) – u(x) · v(x+DX) =

DX DX· v(x+DX) · v(x)

=lim [u(x)+ Du] ·v(x) – u(x) ·[v(x)+Dv] = lim u · v + Du · v – u · v – u · Dv =lim v ·(Du /DX) - u ·(Du /DX)

DX·[v(x)+Dv] · v(x) DX·[v + Dv] · v v · v + v ·Dv

= u’ · v – u · v’

v·v

Так как lim Dv =0 (в силу дифференцируемости, а Þ и непрерывности v(x)), а множители u и v не зависят от Dv.

 

38. Производные элементарных функций.

ТЕОР1: Производная функции f(x)=C выражается формулой Y’=0.

Док-во: Для "х и DX имеем: Df = f (х +DX) – f(x) = C – C = 0. Отсюда Df /DХ = 0/DХ = 0 при "DХ¹0. Þ Y’= lim Df /DX = 0.

ТЕОР2: Производная функции Y=X , где n - целое число, выражается формулой Y’=n ·X .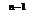

Док-во: Используя формулу бинома Ньютона, имеем

DY= (X+DX) - Х =(Х +n · X 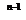· DX +((n(n – 2))/2!) · X ·(DX) +K ·(DX) ) - X = n ·X 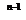· DX + +((n(n – 1))/2!) · X ·(DX) +K·(DX) . Т. о., при DХ¹0

DY/DX = n · X 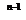+((n(n – 2))/2!) · X ·(DX) + K· (DX) 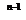. Так как lim DX=0, lim (DX) 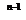=0, то Y’= lim DY/DX = n · X .

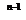ТЕОР3: Производная функции Y=sin X выражается формулой Y’=cos X.

Док-во: Имеем DY= sin(X+DX) – sinX = 2sin(DX/2) · cos(X+DX/2). Т. о., при DХ¹0

DY/DX = 2sin(DX/2) · cos(X+DX/2) = sin(DX/2) · cos(X+DX/2).

DX DX/2

Так как lim sin(DX/2) =1, а lim cos(X+DX/2) = cos X, то Y’= lim DY/DX =cos X.

DX/2

ТЕОР4: Производная функции Y=cos X выражается формулой Y’= -sin X.

Док-во: Имеем DY= cos(X+DX) – cos X = -2sin(DX/2) · sin(X+DX/2). Т. о., при DХ¹0

DY/DX = -2sin(DX/2) · sin(X+DX/2) = - sin(DX/2) · sin(X+DX/2).

DX DX/2

Так как lim sin(DX/2) =1, а lim -sin(X+DX/2) = -sin X, то Y’= lim DY/DX =-sin X.

DX/2

ТЕОР5: Производная функции Y=tg X выражается формулой Y’=1/cos X (X¹p/2+pn, nÎZ).

Док-во: Y’=(tg X)’=(sin X/cos X)’=(sinX)’ ·cosX – sinX· (cosX)’ = cos X + sin X = 1

cos X cos X cos X

ТЕОР6: Производная функции Y=ctg X выражается формулой Y’= -1/sin X (X¹pn, nÎZ).

Док-во: Y’=(ctg X)’=(cos X/sin X)’=(cosX)’ ·sinX – cosX· (sinX)’ = - (sin X + cos X) = -1

sin X sin X sin X

ТЕОР7: Производная функции Y=log X (0<a¹1) выражается формулой Y’=(1/X)·log e=1/(x·ln a).

Док-во: Имеем DY=log (X+DX) - log X = log ((X+DX)/X) = log (1+DX/X). Т. о., при DХ¹0

DY/DX = (1/DX) · log (1+DX/X) = (1/X) · (Х/DX) · log (1+DX/X) = (1/X) · log (1+DX/X) .

Полагая Х/DX=h, имеем: lim (1+DX/X) = lim (1+1/h) =e. Так как логарифмическая функция является непрерывной, то Y’=lim DY/DX =(1/X) · log [lim(1+DX/X) ]= (1/X) · log e = 1/(X·ln a).

СЛЕД: Если Y=log 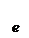X =ln X, то Y’=(1/X).

39. Теорема о производной обратной функции.

ТЕОР1: Если функция Y=f(x) имеет в точке X0 производную f ’(X0) ¹0, то обратная функция X= j(y) также имеет в соответствующей точке Y0 = f(X0) производную, причем j’(Y0) = 1/ f ’(X0).

Док-во: Дадим аргументу Y обратной функции X= j(y) некоторое приращение DY¹0. Функция X=j(y) получит некоторое приращение DX, причем в силу возрастания (или убывания) обратной функции DX¹0. Þ DX /DY=1/(DY/DХ) Перейдем в этом равенстве к пределу при DY®0. Так как обратная функция X= j(y) непрерывна в точке Y, то DX®0 при DY®0. Но при DX®0 предел правой части равенства существует и равен 1/f ’(X0). Þ Существует предел и левой части, который по определению равен j’(Y0). Т. о. получаем j’(Y0) = 1/ f ’(X0).

40. Производные обратных функций.

ТЕОР1: Производная функции Y=a (0<a¹1) выражается формулой Y’ = a ·ln a.

Док-во: Показательная функция Y=a является обратной для логарифмической функции X=log Y. Так как X’(y) = (1/y)· log e, то (по Т о производной обрат Ф) из соотношения log b=1/log a получим Y’(x)=1/X’(Y)=Y/ log e= a ·ln a.

СЛЕД: Если Y=е , то Y’ = е .

ТЕОР2: Производная функции Y=arcsin X выражается формулой Y’=1/ (|X|<1).

Док-во: Так как функция Y=arcsin X определена на интервале –1<X<1, является обратной для функции X=sin Y, определенной в интервале -p/2<Y<p/2 и для функции X=sin Y выполнены все условия теоремы, то по этой теореме функция Y=arcsin X дифференцируема в любой точке X=sin Y и для ее производной в этой точке справедлива формула Y’=(arcsin X)’=1/(sinY)’=1/cosY=1/ . Перед корнем поставим знак “+” в силу того, что cosY положителен на интервале -p/2<Y<p/2. Учитывая, что X=sin Y, окончательно получаем (arcsin X)’=1/ .

ТЕОР3: Производная функции Y=arccos X выражается формулой Y’= -1/ .

Док-во: Так как функция Y=arccos X определена на интервале –1<X<1, является обратной для функции X=cos Y, определенной в интервале 0<Y<p и для функции X=cos Y выполнены все условия теоремы, то по этой теореме функция Y=arccos X дифференцируема в любой точке X=cos Y и для ее производной в этой точке справедлива формула Y’=(arccos X)’=1/(cosY)’= -1/sinY= -1/ . Перед корнем поставим знак “ - ” в силу того, что cosY положителен на интервале 0<Y<p. Учитывая, что X=cos Y, окончательно получаем (arccos X)’= - 1/ .

ТЕОР4: Производная функции Y=arctg X выражается формулой Y’=1/(1+x ).

Док-во: Так как функция Y=arctg X, определена на бесконечной прямой, является обратной для функции X=tg Y определенной на интервале -p/2<Y<p/2, и для функции X=tg Y в окрестности каждой точки интервала -p/2<Y<p/2 выполнены все условия теоремы, то функция Y=arctg X по этой теореме дифференцируема в каждой точке X=tg Y и для ее производной справедлива следующая формула (arctg X)’=1/(tg Y)’=1/(1/cos Y)= cos Y=1/(1+tg Y)= 1/(1+x ).

ТЕОР5: Производная функции Y=arcctg X выражается формулой Y’= -1/(1+x ).

Док-во: Так как функция Y=arcctg X, определена на бесконечной прямой, является обратной для функции Y=ctg X определенной на интервале 0<Y<p, и для функции Y=ctg X в окрестности каждой точки интервала 0<Y<p выполнены все условия теоремы, то функция Y=arcctg X по этой теореме дифференцируема в каждой точке и для ее производной справедлива следующая формула

(arcctg X)’=1/(ctg Y)’=1/(-1/sin Y)= -sin Y= -1/(1+ctg Y)= -1/(1+x ).

 

41. Теорема о производной сложной функции.

ТЕОР: Если функция X= j(t) имеет производную в точке T0, а функция Y=f(x) имеет производную в соответствующей точке X0=j (T0), то сложная функция f[j(t)] имеет производную в точке T0 и справедлива следующая формула: Y’(T0)=f ’(X0) ·j’ (T0).

Док–во: Так как функция Y=f(x) дифференцируема в точке X0, то приращение этой функции в точке X0 может быть записано в виде DY=f ’(X0) ·DX+a(DX)·DX, где lim a(DX)=0. Поделив это равенство на DT (DT¹0), получим DX/DY=f ’(X0) ·DX/DT+a(DX) ·DX/DT. Это равенство справедливо для любых достаточно малых. Возьмем DX равным приращению функции X= j(t), соответствующему приращению DT аргумента t в точке T0, и устремим в этом равенстве DT к 0. Так как по условию X= j(t) имеем в точке T0 производную, то она непрерывна в этой точке. Þ По определению непрерывности функции в точке, DX®0 при DT®0. Но тогда a(DX) ®0, т. е. имеем

lim(a(DX) ·DX/DT)=lim a(DX) ·lim(DX/DT)=0·j’ (T0)=0. В силу этого соотношения существует предел правой части равенства DX/DY=f ’(X0) ·DX/DT+a(DX) ·DX/DT при DT®0, равный f ’(X0) ·j’ (T0). Þ Существует предел при DT®0 и левой части этого равенства, который по определению производной равен производной сложной функции Y=f[j(t)] в точке T0. Т. о., дифференцируемость сложной функции доказана и установлена формула Y’(T0)=f ’(X0) ·j’ (T0).

ЗАМ: теорема справедлива для суперпозиции 3 и более функций.

42. Прием логарифмического дифференцирования. Производная функции Y= , aÎR.

ОПР: Пусть Y=f(x), где X= j(u), U=f(v), V=c(t). Производную Y’(t) следует вычислять по формуле: Y’(t)= f ’(x) ·j’(u) ·f’(v) ·c’(t).

ТЕОР: Производная функции Y=x , где aÎR выражается формулой Y’= a·x .

Док-во: Так как Y=x , то ln Y=a·ln x. Дифференцируя обе части этого равенства по х и используя теорему имеем, Y’/Y=(a·ln x)= a/x. Отсюда, учитывая, что Y=x , получаем Y’=(x )’= a·x .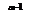

43. Производные высших порядков.

ОПР1: Если производная функции Y=f(x) существует для "xÎX, то можно говорить о существовании производной функции Y’.

ОПР2: Производная от производной I порядка функции Y=f(x) – производная II порядка Y’’=f ’’(x).

ОПР3: Производная от производной II порядка функции Y=f(x) – производная III порядка

Y’’’=f ’’’(x).

ОПР4:Производная n – го порядка функции Y=f(x) – производная от производной n –1 – го порядка Y = (f 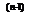(x))’.

44. Дифференциалы высших порядков.

ОПР1: Дифференциал d, взятый от дифференциала dy в точке x в предположении, что dx = dx – дифференциал II порядка функции Y=f(x) в точке x и обозначается d y = f ’’(x)·(dx) .

ОПР2:Дифференциал n-го порядка – дифференциал d, взятый от дифференциала n – 1 -го порядка в предположении, что dx = dx и обозначается d y=f (x)(dx) .

 

45. Возрастание, убывание функции в точке. Достаточное условие возрастания, убывания функции в точке.

ОПР1: Говорят, что функция f(x) возрастает (убывает) в точке C, если найдется такая окрестность точки C, в пределах которой f(x)>f(c) при x>c и f(x)<f(c) при x<c (f(x)<f(c) при x>c и f(x)>f(c) при x<c).

ТЕОР: Если функция f(x) дифференцируема в точке C и f ’(c)>0 (f ’(c)<0), то эта функция возрастает (убывает) в точке C.

Док-во: Докажем для f ’(c)>0. Так как f ’(c) = lim(f(x) – f(c))/(x – c), то по определению предела функции в точке, для ("e>0) ($d>0) такое, что |(f(x) – f(c))/(x – c)|< e при 0<|x – c|<d;

f ’(c) - e< (f(x) – f(c))/(x – c) < f ’(c) + e. Возьмем 0 < e< f ’(c). Тогда f ’(c) - e < 0 и (f(x) – f(c))/(x – c) < 0 при 0<|x – c|<d, а это означает, что всюду в d – окрестности точки C f(x)>f(c) при x>c и f(x)<f(c) при x<c. Возрастание функции f(x) в точке C доказано. (Случай f ’(c)<0 аналогично)

ЗАМ: Это условие является достаточным для возрастания в точке, но не является необходимым.

46. Понятие локального экстремума. Необходимое условие локального экстремума.

ОПР1: Точка X0 – называется точкой строгого локального максимума (минимума) функции f(x), если для всех x из некоторой d окрестности точки X0 выполняется неравенство f(x)<f(X0) (f(x)>f(X0)).

ОПР2: Функция f(x) имеет в точке X0 локальный экстремум, если она имеет в этой точке либо локальный максимум, либо локальный минимум.

ОПР3: Функция f(x) имеет в точке С локальный максимум (минимум), если найдется такая окрестность точки С, в пределах которой значение f(C) является наибольшим (наименьшим) среди всех значений этой функции.

ТЕОР1: Если функция f(x) имеет в точке X0 локальный экстремум и дифференцируема в этой точке, то f(X0)=0.

Док-во: Пусть функция f(x) в точке X0 имеет наибольшее значение, т. е. f(x) £f(X0) для "хÎ(a, b). Это значит, что DY =f(X0+DX) – f(X0) £ 0 для " точки X0+DX Î(a, b). Поэтому, если DX>0 (т. е. x>X0), то DY/DХ£0 и Þ lim DY/DХ£0, т. е. f ’(X0)£0, если же DX<0 (т. е. x<X0), DY/DХ ³0 и Þ lim DY/DХ ³0, т. е. f ’(X0)£0. Получили, что правая производная в точке X0 неположительная, а левая – неотрицательная. По условию f ’(X0), существует и значит, f ’(X0) = f ’(X0) = f ’(X0). Это возможно только в случае, когда f ’(X0) = f ’(X0) = 0. Но тогда f ’(X0) = 0. (Для наименьшего значения аналогично)

Геометрический смысл теоремы Ферма: Если функция f(x)

Поделиться:

Поиск по сайту

©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-11-19 Нарушение авторских прав и Нарушение персональных данных