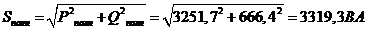Соединение «звезда» с нейтральным проводом.
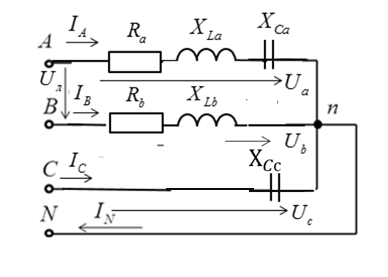
Рис.1
ДАНО
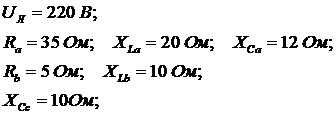
РЕШЕНИЕ
Символический метод
1. Определим напряжения в каждой фазе:
, 
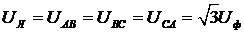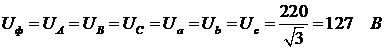
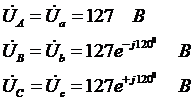
2.Определим комплексные сопротивления фаз:
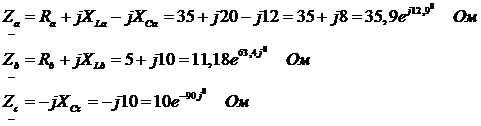
3. Определим фазные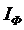 
и линейные токи 
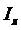(при соединении «звезда» 
)
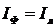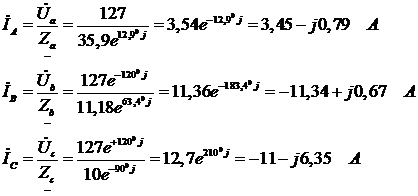
Действующиезначениятоков:
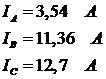
4.Рассчитаем активные мощности каждой линии и всей цепи в целом:
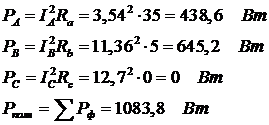
5. Рассчитаем реактивные мощности каждой фазы и всей цепи в целом:
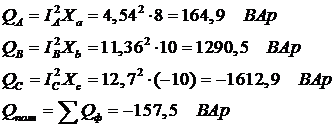
Полная мощность, потребляемая цепью:
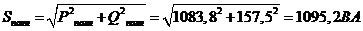
6. Ток в нейтральном проводе:
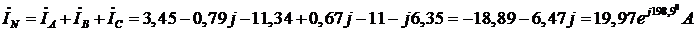
Графоаналитический метод
Определим напряжения в каждой фазе нагрузки (при наличии нейтрального провода с нулевым сопротивлением они равны фазным напряжениям генератора):
,
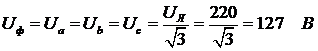Сопротивления фаз нагрузок:
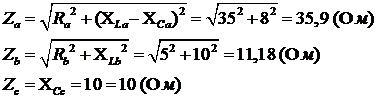
Линейные (фазные) токи:
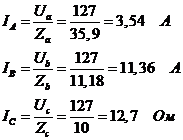
Для определениятока в нулевомпроводенеобходимопостроить векторную диаграмму токов и напряжений
Выбираем масштаб по току: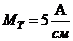 
и масштабом по напряжению: 
.
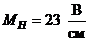Длины векторов:
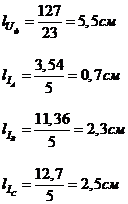
Порядок построения:
Из точки О проводим три вектора фазных напряжений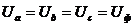 
, углы между которыми 1200
Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений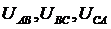 
На диаграмме
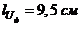
что соответствует условию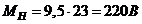 
Откладываем вектора фазных токов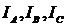 
относительно фазных напряжений на соответственно углы 
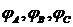, т.е. на углы сдвига фаз между токами и напряжениями соответствующих фаз
где
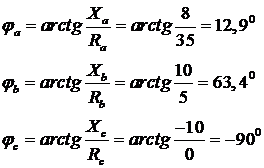
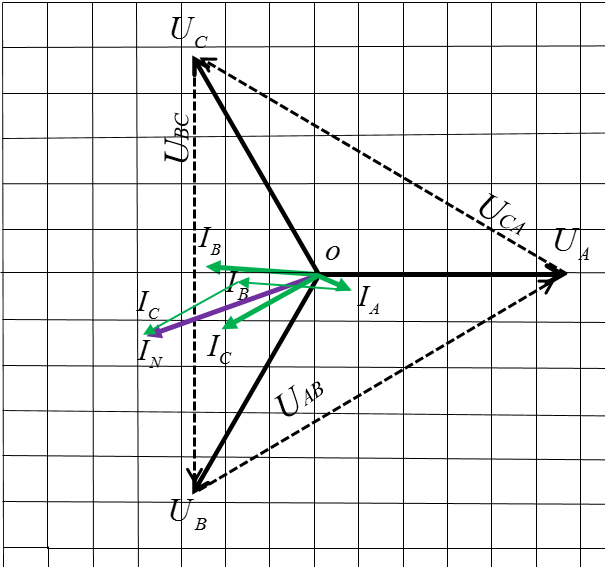
Геометрически складываем фазные токи и получаем ток в нейтральном проводе: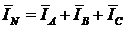 
При геометрическом сложении векторов токов к концу вектора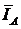 
путем параллельного переноса пристроен вектор 
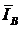К концу вектора 
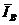пристроен путем параллельного переноса вектор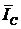 
Точка О соединена с концом вектора 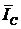-это и есть ток в нулевом проводе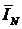 
|
|
Величина тока в нулевом проводе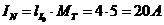 
4Рассчитаем активные мощности каждой линии и всей цепи в целом:
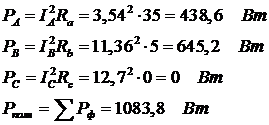
5. Рассчитаем реактивные мощности каждой фазы и всей цепи в целом:
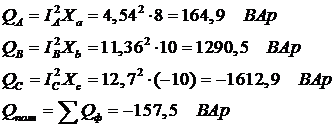
Полная мощность, потребляемая цепью:
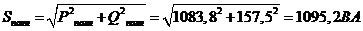
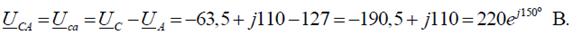
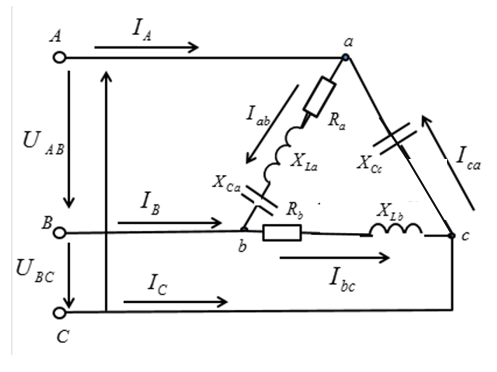
Рис.3
Определим комплексные сопротивления фаз:
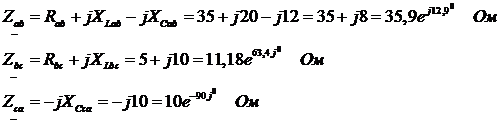
3.Определим фазные токи по закону Ома:
;
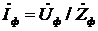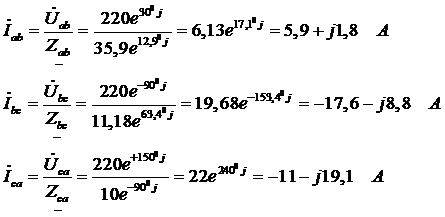
Действующие значения фазных токов:
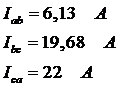
4. Определим линейные токи по первому закону Кирхгофа:
(*)
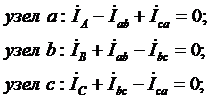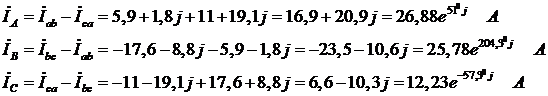
Действующие значения линейных токов:
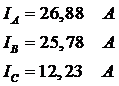
4. Рассчитаем активные мощности каждой линии и всей цепи в целом:
5. Рассчитаем реактивные мощности каждой фазы и всей цепи в целом:
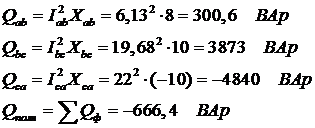
Полная мощность, потребляемая цепью:
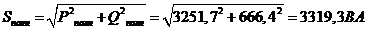
Графоаналитический метод
1. О п р е д е л я е м ф а з н ы е н а п р я ж е н и я.
В данной задаче представлена схема соединения треугольником, значит линейные и фазные напряжения будет равны.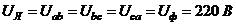 
2. Сопротивления фаз нагрузок:
Сопротивления фаз нагрузок:
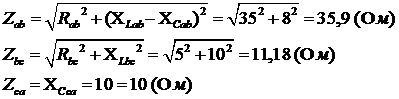
фазныетоки:
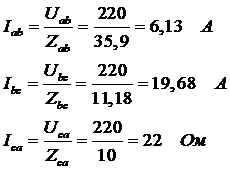
Определяем сдвиг фаз:
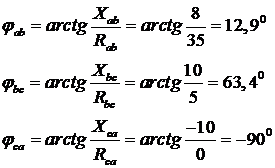
Строим векторную диаграмму в масштабе. Начинаем с построения векторов фазных напряжений, откладывая их друг относительно друга под углом 1200.
Масштаб по напряжению 40 В/ 1см
Зададим масштаб по току 4 А/1 см
Учитывая сдвиг фаз (определен ранее) между током и напряжением в фазах, строим фазные токи.
Учитывая векторную связь между фазными и линейными токами:
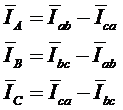
Строим вектора линейных токов.
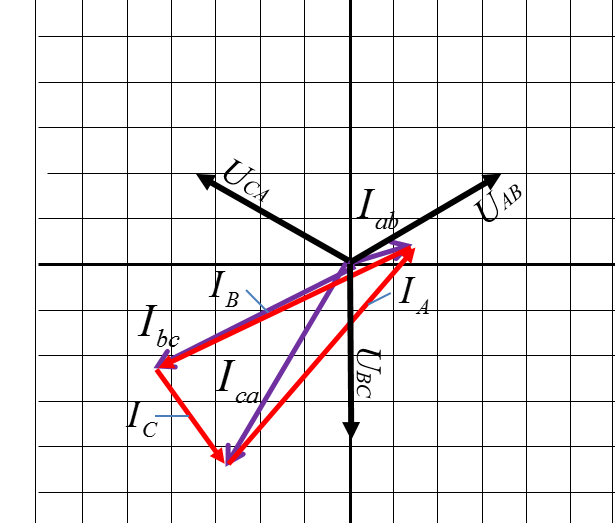
1. По векторной диаграмме, пользуясь масштабом, определяем линейные токи:
IА = 6,7см ∙ 4 A/см = 26,9 А,
IB = 6,45см ∙ 4 A/см =25,8 А,
IC = 3,1 см∙ 4 A/см = 12.2 А
. Рассчитаем активные мощности каждой линии и всей цепи в целом:
|
|
5. Рассчитаем реактивные мощности каждой фазы и всей цепи в целом:
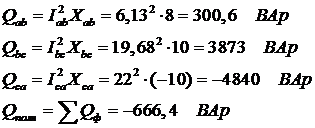
Полная мощность, потребляемая цепью: