Тема: ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Введение
Вращательное движение точек твердого тела характеризуется угловым перемещением φ, угловой скоростью ω = d φ/ dt и угловым ускорением β = d ω/ dt. При вращательном движении все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Перемещение любой точки вращающегося тела за промежуток времени Δ t можно измерить дугой окружности Δ S, пройденной точкой за это время. Выразим угловое перемещение точки тела Δφ в радианах и обозначим r - радиус окружности, описываемой данной точкой вокруг оси вращения, тогда
|
При очень малом угловом перемещении точки тела d φможно заменить малую дугу, пройденную точкой, прямолинейны отрезком dS, тогда
| (1) |
Это равенство устанавливает связь между линейным и угловым перемещением точек вращающегося тела. Линейная и угловая скорости, линейное и угловое ускорения точек вращающегося тела связаны между собой соотношениями:
| (2) |
При поступательном движении перемещение, скорость и ускорение являются векторными величинами (полярные векторы). Во вращательном движении угловое перемещение, угловая скорость и угловое ускорение однозначно определяются лишь тогда, когда известно положение оси вращения в пространстве и указано направление поворота вокруг этой оси. Поэтому эти величины определяются тоже как векторы, направление которых связано с направлением вращения (аксиальные векторы).
Соотношение (2) в векторной форме имеет вид
| (3) |
Для определения направления вектора угловой скорости 
удобно пользоваться правилом буравчика. Вектор угловой скорости направлен по оси вращения в сторону поступательного движения острия буравчика, когда рукоятку его вращают в направлении вращения тела. Направление вектора углового перемещения совпадает с направлением вектора угловой скорости. Если направление оси вращения остается неизменным, вектор углового ускорения 
при увеличении угловой скорости совпадает с ней по направлению, а при уменьшении - направлен в противоположную сторону. При изменении направления оси вращения тела вектор не будет совпадать по направлению с вектором . Поступательное движение твердого тела подчиняется второму закону Ньютона 
, т.е. ускорение 
зависит как от действия силы, так и от массы тела.
|
|
| Рис. 1 |
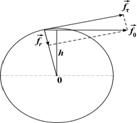
Изменение скорости вращательного движения твердого тела, имеющего закрепленную ось вращения, обуславливается лежащей в плоскости, перпендикулярной к оси вращения, тангенциальной составляющей f τсилы, действующей на тело (рис. 1). При этом угловое ускорение зависит не только от величины этой составляющей силы, но и от плеча. Плечом силы называют кратчайшее расстояние h от оси вращения до линии, вдоль которой действует сила. Поэтому в динамике вращательного движения вместо силы рассматривается момент силы относительно оси вращения.
Моментом силы 
относительно оси вращения называется вектор, модуль которого численно равен произведению силы на плечо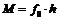 
. Направление вектора момента определяется по правилу буравчика. Если вместо плеча силы воспользоваться радиус-вектором точки приложения силы относительно оси вращения (рис. 1), то момент силы можно представить в виде векторного произведения:
| (4) |
Угловое ускорение вращающегося тела зависит не только от его массы, но и от распределения этой массы относительно оси вращения. Поэтому в динамике вращательного движения вместо массы рассматривают момент инерции тела относительно оси вращения.
Твердое тело можно представить как систему материальных точек. Скалярную величину 
, равную произведению массы материальной точки на квадрат расстояния её от оси вращения, называют моментом инерции материальной точки относительно данной оси. Сумму моментов инерции всех точек тела относительно оси вращения называют моментом инерции относительно оси:
| (5) |
Зависимость углового ускорения тела от момента действующей на тело силы и момента инерции тела относительно неподвижной оси, вокруг которой происходит вращение, определяется основным законом динамики вращательного движения:
| (6) |
Лабораторная работа 3
ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ДЛЯ ВРАЩАЮЩИХСЯ ТЕЛ
Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: «Закон динамики вращательного движения твердого тела»
Цель работы. Второй закон Ньютона для вращающегося тела записывается формулой (6). В работе требуется экспериментально подтвердить:
1) при неизменном моменте инерции системы J угловое ускорение пропорционально моменту действующей силы β ~ M ;
2) при постоянном моменте силы действующей на тело M угловое ускорение обратно пропорционально моменту инерции тела β ~ 1/ J
В работе также требуется определить моменты инерции маятника для трех положений грузов.
Физическое обоснование эксперимента и описание экспериментальной установки
|
| Рис. 3.1 |
Лабораторная работа выполняется на крестообразном маятнике Обербека (рис. 3.1). Установка «Маятник Обербека» ФМ – 14М вместе с цифровым измерителем временных интервалов ФМ – 1/1 обеспечивает возможность определения собственного момента инерции маятника Обербека и установление зависимости углового ускорения от момента инерции тела.
Вращающаяся часть установки состоит из четырех спиц, закрепленных во втулке под прямым углом друг к другу. На ось втулки насажены два легких шкива различных радиусов (R 1 и R 2). Вращение происходит вокруг горизонтальной оси.
Момент инерции системы относительно оси вращения можно изменять либо меняя массы грузов, закрепленных на спицах, либо перемещая грузы вдоль спиц. Каждый раз, закрепляя грузы на спицах на определенном расстоянии от оси вращения, необходимо проверить, правильно ли сбалансирована система, т.е. находится ли она в положении безразличного равновесия.
Момент силы, вызывающий вращение маятника, создается натяжением нити, навитой на один из шкивов установки, под действием груза Р.
Момент силы можно изменить, подвешивая к нити грузы различного веса или изменяя плечо силы, для чего нить закрепляется на шкивах разного диаметра.
Под действием груза P нить разматывается и приводит во вращение крестовину маятника. Измеряя время t, в течение которого груз P из состояния покоя опустился на расстояние H, можно определить линейное ускорение груза
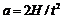
| (3.1) |
Измерив радиус шкива R и пользуясь соотношением (2), можно найти угловое ускорение маятника
| (3.2) |
Если f н - сила натяжения нити, а P = mg - вес груза, то справедливо соотношение ma = P - f н
Следовательно, вращающий момент M равен
| (3.3) |
где R – радиус шкива, m – масса груза.
Это выражение справедливо, если можно пренебречь силами трения, т.е. если можно считать, что момент сил трения M тр << M н. В действительности это не выполняется, и момент сил трения играет заметную роль, в этом случае следует рассматривать вращающий момент как разность моментов создаваемых силой натяжения и силами трения M = M н - M тр.
Порядок выполнения работы
1. Закрепить грузы на спицах у самой оси вращения. Измерить высоту Н. Измерить радиусы шкивов, на которые наматывается нить R 1 и R 2 с помощью штангенциркуля. Намотать нить на шкив с радиусом R 1 Измерить время прохождения расстояния Н для изначально закрепленного на нити груза с добавляемым грузом, используя, прилагаемый к установке цифровой измеритель временных интервалов ФМ – 1/1. Цифровой измеритель должен быть предварительно включен в сеть 220 В.
Провести измерения времени падения 5-10 грузов.
Чтобы момент сил трения был постоянным, масса груза вместе с первоначальным грузом, на котором он лежит, не должна быть больше 120 ÷ 130 г.
Результаты измерений и результаты их последующей обработки поместить в таблицу.
Таблица 3.1
| m i | t 1 | t 2 | … | t i | t ср | a | β | M н | M тр | M |
| m 1 | ||||||||||
| … | ||||||||||
| m 5 |
2. Вычислить величины a, β и M н по формулам (3.1), (3.2) и (3.3) соответственно для всех грузов.
Построить график зависимости углового ускорения β от действующего момента силы M н. Эта зависимость должна быть линейной. Отрезок, отсекаемый прямой на оси абсцисс, должен быть равен моменту сил трения. Определив из графика M тр, вычислить истинный момент M = M н - M тр. Зависимость β = f (M) при J 1 = const обработать по методу наименьших квадратов, определив тангенс угла наклона прямой к оси абсцисс. Величина, обратная тангенсу угла наклона, равна моменту инерции маятника J 1.
3. Сместить грузы на спицах маятника на концы спиц. Повторить такие же измерения, изменяя момент силы, действующей на маятник.
Результаты поместить в таблицу аналогичную таблице 3.1. Полученные результаты нанести в таком же масштабе на предыдущий график. Вычислить момент инерции маятника J 2.
4. Грузы передвинуть и закрепить в середине спиц таким образом, чтобы маятник находился в положении безразличного равновесия. Все измерения и расчеты повторить, построить график и вычислить момент инерции маятника J 3.
5. На построенных графиках зависимости, β = f (M) взять три значения момента силы M. Для каждого выбранного значения M найти из графиков величины β1, β2, β3, соответствующие трем моментам инерции. Построить графики зависимости β = f (1/J) при M = const. Зависимости должны быть линейными.
Аналогичным образом выполнить задания по пунктам 1 – 5, намотав нить на шкив с радиусом R 2, т.е. тем самым изменить момент силы, изменяя плечо силы.
Выбор объема выполняемых студентом заданий в данной лабораторной работе определяет преподаватель.