1. Укажите правильное утверждение:
1. Случайное событие, это событие которое может не произойти, если изменятся условия опыта.
2. Случайное событие, это такое событие, которое зависит от случая.
3. Событие, которое в данных условиях может произойти или не произойти называется случайным. *
2. Укажите правильное утверждение:
1. Случайное событие называется достоверным, если в результате данного испытания оно обязательно происходит. *
2. Случайное событие называется достоверным, если оно может произойти или не произойти в данных условиях.
3. Случайное событие называется достоверным, если в результате данного испытания оно обязательно не происходит.
3. Укажите правильное утверждение:
1. Случайное событие называется невозможным, если в данных условиях оно может произойти или не произойти.
2. Случайное событие называется невозможным, если оно не происходит при изменении условий опыта.
3. Случайное событие, которое в данных условиях произойти не может, называется невозможным.*
4. Укажите правильное утверждение:
1. Два события называются совместными, если вероятность появления одного из них зависит от того, произошло или не произошло второе.
2. Два события называются совместными, если появление одного из них не исключает появление другого. *
3. Примером совместных событий может служить: одновременное выпадение герба и решки при бросании двух монет.
5. Укажите правильное утверждение:
1. События А и В называются противоположными, если появление события А исключает появление события В ( ).
).
2. Событие В, происходящее тогда и только тогда, когда не происходит событие А, называется противоположным событию А ( ).*
).*
3. Событие В, происходящее тогда и только тогда, когда может не произойти событие А, называется противоположным последнему ( ).
).
6. Укажите правильное утверждение:
1. Два события А и В называются несовместными, если при появлении одного из них не всегда происходит другое.*
2. Два события А и В называются несовместными, если появление одного из них исключает появление другого.
3. Два события А и В называются совместными, если при появлении одного из них всегда происходит другое.
7. Укажите правильное утверждение:
1. Классической вероятностью события А называется отношение общего числа элементарных событий к числу случаев, в которых произошло событие А.
2. Классической вероятностью события А называется отношение числа m элементарных событий, благоприятствующих появлению события А, к общему числу всех возможных элементарных исходов n. *
3. Классической вероятностью события А называется отношение числа появившихся в испытании событий m к общему числу всех возможных элементарных исходов n.
8. Относительной частотой появления события А называется:
1. Отношение общего числа элементарных событий к числу случаев, в которых произошло событие А.
2. Отношение числа m элементарных событий, благоприятствующих появлению события А, к общему числу всех возможных элементарных исходов n.
3. Отношение числа случаев, в которых произошло событие А, к общему числу проведенных опытов. *
9. Укажите правильное утверждение:
1. Под вероятностью события А, в статистическом смысле, понимают почти достоверный предел, к которому стремится относительная частота появления событие А при увеличении числа проведенных опытов n.*
2. Под вероятностью события А, в статистическом смысле, понимают почти достоверный предел, к которому стремится относительная частота появления события А при неограниченном числе появлений события А.
3. Под вероятностью события А, в статистическом смысле, понимают почти относительную частоту появления событие А при проведении опытов.
10. Укажите правильное утверждение:
1. События А и В называются зависимыми, если при проведении испытаний вероятности их изменяются.
2. Событие А называется зависимым от события В, если вероятность наступления события В зависит от того наступило или нет событие А.
3. Событие В называется зависимым от события А, если вероятность наступления события В зависит от того наступило или нет событие А.*
11. Укажите правильное утверждение:
1. Суммой событий А и В называют событие С, заключающееся в том, что в результате испытаний наступит или событие А, или событие В, или они наступят оба. *
2. Суммой событий А и В называют событие С, заключающееся в том, что в результате испытаний может наступить одно из этих событий.
3. Суммой событий А и В называют событие С, заключающееся в том, что наступят и событие А, и событие В одновременно.
12. Укажите правильное утверждение:
1. Вероятность наступления двух несовместных событий А и В равна сумме вероятностей этих событий: Р(АВ) = Р(А) + Р(В).
2. Вероятность наступления хотя бы одного из двух несовместных событий, безразлично которого, равна сумме их вероятностей: Р(А или В) = Р(А) + Р(В).*
3. Вероятность появления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий, без вероятности их совместного появления: Р(А+В) = Р(А) + Р(В) - Р(АВ).
13. Укажите правильное утверждение:
1. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий, умноженной на вероятность их совместного появления: Р(А или В) = (Р(А) + Р(В)) * Р(АВ).
2. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий, без вероятности их совместного появления: Р(А+В) = Р(А) + Р(В) - Р(АВ).*
3. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий и вероятности их совместного появления:
Р(А+В) = Р(А) + Р(В) + Р(АВ).
14. Укажите правильное утверждение:
1. Условная вероятность - это вероятность зависимого события.
2. Условная вероятность - это вероятность события В при условии, что произошло событие А: РА(В) или Р(В/А). *
3. Условная вероятность - это вероятность события, А заключающееся в том, что событие В может произойти или не произойти.
15. Укажите правильное утверждение:
1. Вероятность совместного появления двух зависимых событий или А, или В равна сумме вероятностей этих событий: Р(А или В) = Р(А) + Р(В).
2. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого: Р(АВ) = Р(А) * РА(В). *
3. Вероятность совместного появления двух зависимых событий А и В равна поизведению вероятностей этих событий: Р(А и В) = Р(А)·Р(В).
16. Укажите правильное утверждение:
1. Вероятность совместного появления двух и более независимых случайных событий А и В определяется произведением вероятностей этих событий: Р(А и В) = Р(А) * Р(В). *
2. Вероятность появления двух и более независимых случайных событий А или В определяется произведением вероятностей этих событий:
Р(А или В) = Р(А) * Р(В).
3. Вероятность произведения двух или более независимых событий равна произведению вероятностей этих событий на их условную вероятность.
17. Укажите правильное утверждение:
1. Для произведения вероятностей зависимых событий справедливо выражение: Р(АВ) = Р(А) * Р(В) - Р(АВ).
2. Для произведения вероятностей зависимых событий справедливо выражение: Р(А) * РА(В) = Р(В) * РВ(А). *
3. Для произведения вероятностей зависимых событий справедливо выражение: (АВ) = Р(А) · Р(В).
18. Укажите правильное утверждение:
1. Формула Бернулли позволяет найти вероятность того, что при n независимых испытаниях событие А может наступить m раз.
2. Формула Бернулли позволяет найти вероятность того, что при n независимых испытаниях по схеме Бернулли событие А наступит m раз. *
3. Формула Бернулли позволяет найти вероятность того, что при любых n независимых испытаниях событие А наступит n раз.
19. Формула Бернулли имеет вид:
1. 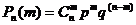 *
*
2. 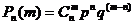
3. 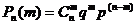
20. При большом числе проведенных опытов и малой вероятности появления события в отдельном опыте пользоваться формулой Бернулли затруднительно, поэтому:
1. Приближенно пользуются статистической вероятностью.
2. Приближенно пользуются формулой Байеса.
3. Приближенно пользуются формулой Пуассона.*
21. Случайной величиной называют такую величину, которая:
1. В результате испытания может принять различные значения, при этом заранее неизвестно какие именно. *
2. В результате испытания примет одно и только одно возможное значение, при этом заранее неизвестно, какое именно.
3. В результате испытания примет одно и только одно возможное значение, при этом заранее неизвестно, какое именно.
22. Дискретной (прерывной) называют случайную величину,
1. Которая принимает отдельные возможные значения с определенными вероятностями, которые можно пронумеровать.*
2. Вероятность которой принимает любые значения из интервала от 0 до 1, называют непрерывной.
3. Для которой все ее возможные значения целиком заполняют некоторый конечный или бесконечный промежуток.
23. Непрерывной называют случайную величину,
1. Которая принимает отдельные возможные значения с определенными вероятностями, которые можно пронумеровать.
2. Вероятность которой принимает любые значения из интервала от 0 до 1, называют непрерывной.
3. Для которой все ее возможные значения целиком заполняют некоторый конечный или бесконечный промежуток. *
24. Выбрать правильный пример:
1. В качестве примера дискретной случайной величины можно использовать результаты измерения роста студентов в группе или на курсе.
2. В качестве примера дискретной случайной величины можно использовать результаты большого числа бросаний игральной кости. *
3. В качестве примера дискретной случайной величины можно использовать результаты большого числа бросаний игральной кости.
25. Выбрать правильный пример:
1. В качестве примера непрерывной случайной величины можно использовать результаты измерения роста студентов в группе или на курсе*
2. В качестве примера непрерывной случайной величины можно использовать результаты большого числа бросаний игральной кости.
3. В качестве примера непрерывной случайной величины можно использовать результаты большого числа бросаний игральной кости.
26. Законом распределения дискретной случайной величины называют:
1. Соответствие между ее возможными значениями и их вероятностями. *
2. Функциональную зависимость между ее значениями и плотностью вероятности случайной величины.
3. Соответствие между значениями случайной величины и соответствующими математическими ожиданиями.
27. К числовым характеристикам дискретной случайной величины относят:
1. Среднее арифметическое и доверительный интервал.
2. Математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану. *
3. Математическое ожидание, вероятность появления случайной величины, закон распределения, моду, медиану.
28. Математическим ожиданием М(Х) дискретной случайной величины Х называется:
1. Сумма произведений всех возможных значений случайной величины на соответствующие вероятности. *
2. Произведение значения случайной величины на ее вероятность.
3. Сумма всех возможных значений случайной величины.
29. Математическое ожидание дискретной случайной величины может быть представлено выражением:
1. М(Х) = m = х1р1 - х2р2 -... - хnрn.
2. М(Х) = m = х1р1 + х2р2 +... + хnрn.*
3. М(Х) = m = х1р1 * х2р2 *... * хnрn.
30. Модой М0 дискретного распределения называют такое значение хm дискретной случайной величины,:
1. Что предшествующее и следующее за ним значения имеют вероятность меньше Р(хm).*
2. Которое больше других по абсолютной величине.
3. Которое расположено в центре ряда распределения.
31. Медианой Ме дискретного распределения называют такое значение хm дискретной случайной величины,:
1. Что предшествующее и следующее за ним значения имеют вероятность меньше Р(хm).
2. Которое больше других по абсолютной величине.
3. Которое расположено в центре ряда распределения. *
32. Если распределение задано следующей таблицей, то мода М0 равна:
| X | |||||||||
| P | 0,181 | 0,220 | 0,241 | 0,038 | 0,090 | 0,071 | 0,070 | 0,032 | 0,048 |
1. М0= 4.
2. М0= 2.*
3. М0= 8.
33. Если распределение задано следующей таблицей, то медиана Ме равна:
| X | |||||||||
| P | 0,181 | 0,220 | 0,241 | 0,038 | 0,090 | 0,071 | 0,070 | 0,032 | 0,048 |
1. Ме= 4.*
2. Ме= 2.
3. Ме= 8.
34. Дисперсией дискретной случайной величины называют:
1. Математическое ожидание квадрата этой случайной величины.
2. Математическое ожидание квадрата отклонения этой случайной величины от ее математического ожидания. *
3. Математическое ожидание квадрата суммы этой случайной величины и ее математического ожидания.
35. Дисперсия дискретной случайной величины может быть представлена выражением:
1. D(x) = M(Xср. - m)2.
2. D(x) = M(Xср. + m)2.
3. D(x) = M(X - m)2. *
36. Средним квадратическим отклонением случайной величины называется:
1. Корень квадратный из дисперсии.*
2. Квадрат дисперсии.
3. Корень квадратный из среднего арифметического.
37. Функцией распределения случайной величины Х, называется функция F(x), равная вероятности того, что случайная величина Х:
1. Приняла значение хi большее х: F(x) = P(X > x).
2. Приняла значение хi меньшее х: F(x) = P(X < x). *
3. Приняла наперед заданное значение хi, равное х: F(x) = P(X = x).
38. Функцией плотности распределения вероятности (или, короче, функцией плотности распределения) называется такая функция f(x):
1. Для которой первообразной будет функция распределения F(x):  .
.
2. Для которой производной будет функция распределения F(x):  .
.
3. Для которой первообразной будет функция распределения F(x):  . *
. *
39. Математическое ожидание непрерывной случайной величины может быть вычислено по формуле:
1. 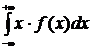 *
*
2. 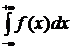
3. 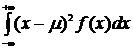
40. Дисперсия непрерывной случайной величины может быть вычислено по формуле:
1. 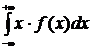
2. 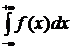
3. 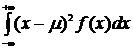 *
*
41. Среднее квадратическое отклонение непрерывной случайной величины может быть вычислено по формуле:
1. 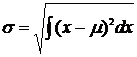
2. 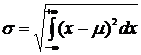 *
*
3. 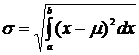
42. Вероятность попадания случайной величины Х в интервал (а, в) может быть вычислена по формуле:
1. 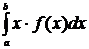
2.  *
*
3. 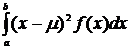
43. Случайная величина распределена по биномиальному закону, если вероятность вычисляется
1. по формуле Бернулли*
2. по теореме сложения вероятностей
3. по теореме умножения вероятностей
44. Случайная величина распределена равномерно, если
1. Все ее значения равномерно распределены вдоль числовой прямой
2. Все значения имеют одинаковую вероятность
3. Функция плотности вероятности задается постоянной величиной на всём отрезке определения случайной величины*
45. Равномерно распределенная случайная величина может быть задана
1. На любом числовом интервале
2. Только на ограниченном числовом интервале*
3. Только на всей числовой прямой
46. Числовые характеристики равномерно распределенной случайной величины определяются
1. Границами интервала, в котором задана случайная величина*
2. Вероятностью, с которой задана случайная величина
3. Длиной интервала, в котором задана случайная величина
47. Математическое ожидание равномерно распределенной величины вычисляется по формуле
1.  *
*
2. 
3. 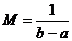
48. Закон распределения непрерывной случайной величины называют нормальным, если распределение ее плотности вероятности подчиняется:
1. Закону Гаусса.*
2. Закону Бернулли.
3. Равномерному закону.
49. Закон распределения непрерывной случайной величины называют нормальным, если распределение ее плотности вероятности подчиняется закону Гаусса, и описывается уравнением:
1. 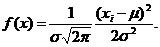
2. 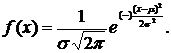 *
*
3. 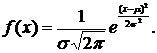
50. Укажите правильное утверждение для стандартных интервалов:
1. Интервал (± s), относительно математического ожидания для нормально распределенной случайной величины, является первым стандартным интервалом с вероятностью попадания в него Р = 0,68. *
2. Интервал (± 2s), относительно дисперсии нормально распределенной случайной величины, является вторым стандартным интервалом с вероятностью попадания в него
Р = 0,95.
3. Интервал (±3s), относительно математического ожидания для нормально распределенной случайной величины, является вторым стандартным интервалом с вероятностью попадания в него Р = 0,99.
Для заметок