Вариант № база.
1. Найдите значение выражения 
Решение.
Найдём значение выражения:

Ответ: 2,33.
2. Найдите значение выражения 
Решение.
Преобразуем выражение:

Ответ: 9
3. В выборах участвовали два кандидата. Голоса избирателей распределились между ними в отношении 3:2. Сколько процентов голосов получил проигравший?
Решение.
Найдём количество процентов в одной части:

Найдём количество процентов голосов в двух частях:
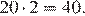
Ответ: 40.
4. Найдите  из равенства
из равенства 
 а
а 
Решение.
Выразим  из равенства и найдём значение выражения:
из равенства и найдём значение выражения:

Ответ: 0,1.
5. Найдите значение выражения  .
.
Решение.
Выполним преобразования:
 .
.
Ответ: 18.
6. В старинной книге полезных советов «Домострой» имеется рецепт десерта Шарлотка. Для приготовления Шарлотки следует взять 12 фунтов яблок. Сколько килограммов яблок надо взять хозяйке для приготовления Шарлотки? Считайте, что 1 фунт равен 400 граммам.
Решение.
В 12 фунтах содержится 12 · 400 = 4800 граммов или 4,8 килограмма.
Ответ: 4,8.
7. Найдите корень уравнения 
Решение.
Найдём корень уравнения:

Ответ: 2.
8.  План местности разбит на клетки. Каждая клетка обозначает квадрат 10 м × 10 м. Найдите площадь участка, изображённого на плане. Ответ дайте в м2.
План местности разбит на клетки. Каждая клетка обозначает квадрат 10 м × 10 м. Найдите площадь участка, изображённого на плане. Ответ дайте в м2.
Решение.
Участок, изображенный на плане, представляет собой трапецию, площадь которой равна произведению полусуммы оснований на высоту. Таким образом площадь участка:

Ответ: 900.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ | |
| А) рост ребёнка Б) толщина листа бумаги В) длина автобусного маршрута Г) высота жилого дома | 1) 32 км 2) 30 м 3) 0,2 мм 4) 110 см |
Решение.
Рост ребёнка может быть равен 110 см, толщина листа бумаги может составлять 0,2 мм, длина автобусного маршрута — 32 км, высота жилого дома — 30 м.
Ответ: 4312.
10. У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Решение.
У Вити в копилке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Больше 70 рублей останется, если достать из копилки либо рублёвую, либо двухрублёвую монету. Искомая вероятность равна 18: 25 = 0,72.
Ответ: 0,72.
11. На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат — крутящий момент в Н  м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 60 Н
м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 60 Н  м. Какое наименьшее число оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение?
м. Какое наименьшее число оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение?

Решение.
Из графика видно, что крутящий момент 60 Н  м достигается при 2000 оборотов двигателя в минуту (см. рисунок).
м достигается при 2000 оборотов двигателя в минуту (см. рисунок).
Ответ: 2000.
12. В первом банке один фунт стерлингов можно купить за 47,4 рубля. Во втором банке 30 фунтов — за 1446 рублей. В третьем банке 12 фунтов стоят 561 рубль. Какую наименьшую сумму (в рублях) придется заплатить за 10 фунтов стерлингов?
Решение.
Рассмотрим все варианты.
В первом банке 10 фунтов стерлингов будут стоить 47,4  10 = 474 руб.
10 = 474 руб.
Во втором банке 10 фунтов стерлингов стоят 1446: 3 = 482 руб.
В третьем банке 1 фунт стерлингов стоит 561: 12 = 187: 4 = 46,75 руб. Значит, 10 фунтов стерлингов будут стоить 46,75  10 = 467,5 руб.
10 = 467,5 руб.
Ответ: 467,5.
13.  Пирамида Снофру имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 220 м, а высота — 104 м. Сторона основания точной музейной копии этой пирамиды равна 44 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
Пирамида Снофру имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 220 м, а высота — 104 м. Сторона основания точной музейной копии этой пирамиды равна 44 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
Решение.
Переведём сантиметры в метры и найдём во сколько раз сторона основания пирамиды отличается от музейной копии:

Найдём высоту музейной копии:

Ответ: 20,8.
14. На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ | |
| А) зима Б) весна В) лето Г) осень | 1) Ежемесячный объём продаж был меньше 40 штук в течение всего периода. 2) Ежемесячный объём продаж достиг максимума. 3) Ежемесячный объём продаж падал в течение всего периода. 4) Ежемесячный объём продаж рос в течение всего периода. |
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
Решение.
А) зима: из графика видно, что ежемесячный объём продаж достиг максимума (150 шт) - вариант 2
Б) весна: из графика видно, что ежемесячный объём падал в течение всего периода - вариант 3
В) лето: из графика видно, что ежемесячный объём продаж был меньше 40 штук в течение всего периода - вариант 1
Г) осень: из графика видно, что ежемесячный объём продаж рос в течение всего периода - вариант 4
Ответ: 2314
15.  Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.
Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.
Решение.
Площадь квадрата вычисляется по формуле:  . Площадь ромба вычисляется по формуле:
. Площадь ромба вычисляется по формуле:  Таким образом:
Таким образом: 
Ответ: 32.
16.  Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна  .
.
Решение.
Объем пирамиды равен
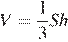 ,
,
где  – площадь основания, а
– площадь основания, а 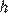 – высота пирамиды. Площадь равностороннего треугольника в основании
– высота пирамиды. Площадь равностороннего треугольника в основании
 ,
,
Тогда объем пирамиды равен
 .
.
Ответ: 0,25.
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А)  Б)
Б) 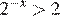 В)
В)  Г)
Г) 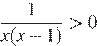
| 
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение.
Решим неравенства:
А) 
Б) 
В) 
Г) 
Ответ: 3241.
18. Каждый раз, когда Надя приезжает в деревню к бабушке в гости, бабушка заплетает ей косички. Также Надя заплетает себе косички всегда, когда идёт на физкультуру. Выберите утверждения, которые верны при приведённых условиях.
1) Каждый раз, когда у Нади заплетены косички, она находится в деревне.
2) Если Надя без косичек, значит, она не у бабушки в гостях.
3) Если Надя без косичек, значит, сегодня физкультура.
4) Когда Надя сдаёт норматив по бегу на физкультуре, она с косичками.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение.
Проанализируем представленные утверждения, исходя из условий задачи.
1) Не всегда, Надя также заплетает косички, когда идёт на физкультуру. Утверждение неверно.
2) Если Надя приезжает в деревню, бабушка заплетает ей косички. Утверждение верно.
3) Надя заплетает себе косички всегда, когда идёт на физкультуру. Утверждение неверно.
4) Надя заплетает себе косички всегда, когда идёт на физкультуру. Утверждение верно.
Ответ: 24.
----------
Дублирует задание 513785.
19. Найдите четырёхзначное натуральное число, кратное 19, сумма цифр которого на 1 больше их произведения.
Решение.
Если хотя бы одна цифра в записи числа — нуль, то произведение цифр равно 0, а тогда их сумма равна 1. Единственное такое четырёхзначное число — 1000, но оно не кратно 19. Поэтому нулей среди цифр нет. Отсюда следует, что все цифры не меньше 1, и их сумма не меньше четырёх, а значит, произведение цифр не меньше трёх. Чтобы произведение было не меньше трёх хотя бы одна из цифр должна быть больше 1. Рассмотрим такие числа в порядке возрастания суммы их цифр.
Если сумма цифр равна 5, то число записывается одной двойкой и тремя единицами (это числа 1112, 1121, 1211, 2111). Произведение цифр равно 2, поэтому они не удовлетворяют условию.
Если сумма цифр равна 6, то число записывается одной тройкой и тремя единицами или двумя двойками и двумя единицами (это числа 1113, 1131, 1311, 3111, 1122, 1212,...). Произведение цифр равно 3 или 4 соответственно, поэтому такие числа не удовлетворяют условию.
Если сумма цифр равна 7, то произведение должно быть равно 6. Это выполнено для чисел, записываемых тройкой, двойкой и двумя единицами. Поскольку число 3211 кратно 19, оно и является искомым.
Ответ: 3211.
Примечание.
Четырёхзначное число, обладающее требуемыми свойствами, единственно. Покажем это, приведя другое решение.
Приведём решение Дмитрия Мухина (Москва).
Пусть a, b, c, d — цифры числа и пусть а самая большая из них (порядок цифр не важен). Покажем, что произведение меньших цифр не больше четырёх. Действительно, из равенства a + b + c + d = 1 + abcd, получаем 4 a ≥ abcd + 1. Деля на наибольшую цифру a, получаем, что bcd < 4.
Рассмотрим теперь следующие случаи.
1. Пусть среди чисел b, c, d есть нуль, тогда поскольку a + b + c + d = 1, это число 1000, но оно на 19 не делится. Итак, все три меньшие цифры числа отличны от нуля.
2. Пусть все три меньшие цифры равны единице, тогда a + 3 = a + 1. Этот случай невозможен.
3. Пусть меньшие цифры это две единицы и двойка. Тогда a + 4 = 2 a + 1, откуда a = 3. Перебирая 12 чисел, составленных из цифр 1, 1, 2, 3, находим, что из них кратно 19 только число 3211. Оно и является ответом.
4. Пусть меньшие цифры это две единицы и тройка. Тогда a + 5 = 3 a + 1. Отсюда a = 2, но тогда a не наибольшая цифра. Противоречие.
Поскольку bcd < 4, других вариантов нет. Искомое число единственно, оно равно 3211.
20. В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
Решение.
Груздей максимум 16 (иначе можно было бы взять 17 груздей и условие бы не выполнилось). Рыжиков максимум 24 (иначе можно было бы взять 25 груздей в нарушение условия). Известно, что в корзине всего 40 грибов. Поэтому груздей ровно 16, а рыжиков ровно 24.
Ответ: 24.
Вариант № профиль.
1. В школе французский язык изучают 124 учащихся, что составляет 25% от числа всех учащихся школы. Сколько учащихся в школе?
Решение.
Разделим 124 на 0,25:

Значит, в школе учится 496 учеников.
Ответ: 496.
2. На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с 17 по 31 августа 2004 года. По горизонтали указываются числа месяца, по вертикали — цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену нефти на момент закрытия торгов в указанный период (в долларах США за баррель).

Решение.
Из графика видно, что наименьшая цена за баррель нефти составляла 39 долларов США (см. рисунок).
Ответ: 39.
3. Найдите площадь треугольника, вершины которого имеют координаты (2; 2), (8; 10), (8; 8).
Решение.

Длина стороны, соединяющий вершины с координатами (8; 10) и (8; 8), равна 2. Высота, проведенная из вершины с координатами (2; 2) к продолжению этой стороны, равна 6. Поэтому площадь треугольника равна половине произведения высоты на сторону, к которой она проведена. Поэтому площадь равна 6.
Ответ: 6.
4. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение.
За первые три дня будет прочитан 51 доклад, на последние два дня планируется 24 доклада. Поэтому на последний день запланировано 12 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 
Ответ: 0,16.
5. Найдите корень уравнения 
Решение.
Последовательно получаем:

Ответ: 21.
6. 
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Решение.
Площадь треугольника равна произведению его полупериметра (p) на радиус вписанной окружности (r):

Ответ: 6.
7.  На рисунке изображён график функции
На рисунке изображён график функции  и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.
и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.
Решение.
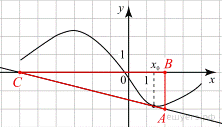 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:

Ответ: − 0,25.
8. 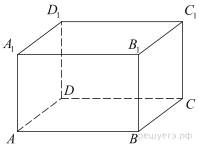 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  , у которого
, у которого  ,
,  ,
, 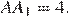
Решение.
 Основанием пирамиды, объем которой нужно найти, является половина боковой грани пареллелепипеда, а высотой пирамиды является ребро параллелепипеда
Основанием пирамиды, объем которой нужно найти, является половина боковой грани пареллелепипеда, а высотой пирамиды является ребро параллелепипеда  Поэтому
Поэтому

Ответ: 10.
9. Найдите значение выражения 
Решение.
Выполним преобразования:

Ответ: −0,5.
10. Плоский замкнутый контур площадью  м
м  находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой
находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой  , где
, где  – острый угол между направлением магнитного поля и перпендикуляром к контуру,
– острый угол между направлением магнитного поля и перпендикуляром к контуру,  Тл/с – постоянная,
Тл/с – постоянная,  – площадь замкнутого контура, находящегося в магнитном поле (в м
– площадь замкнутого контура, находящегося в магнитном поле (в м  ). При каком минимальном угле
). При каком минимальном угле  (в градусах) ЭДС индукции не будет превышать
(в градусах) ЭДС индукции не будет превышать  В?
В?
Решение.
Задача сводится к решению неравенства  на интервале
на интервале  при заданных значениях площади контура
при заданных значениях площади контура  и постоянной
и постоянной  Тл/с:
Тл/с:

Ответ: 60.
11. Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Решение.
Пусть плиточник должен был укладывать  кв. м плитки в течение
кв. м плитки в течение  дней. Если он будет укладывать
дней. Если он будет укладывать  кв. м плитки в течение
кв. м плитки в течение  дней, то выполнит ту же работу. Поскольку всего нужно уложить 175 кв. м плитки, имеем систему уравнений:
дней, то выполнит ту же работу. Поскольку всего нужно уложить 175 кв. м плитки, имеем систему уравнений:

Таким образом, плиточник планировал в течение 7 дней укладывать по 25 кв. м плитки в день.
Ответ: 25.