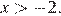Пусть плиточник должен укладывать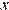 
кв. м плитки в день и справиться с работой за 
дней. Если укладывать 
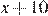кв. м плитки в день, то работа будет выполнена за 
дня. Имеем:
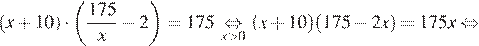
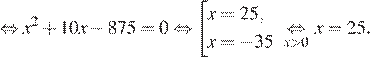
Таким образом, плиточник должен укладывать по 25 кв. м плитки в день.
Приведём другое решение.
Пусть плиточник должен был укладывать x кв. м плитки в день. Тогда он уложит всю плитку за 
дней. Если бы он укладывал на 10 кв. м в день больше, то уложил бы плитку на два дня раньше и сделал это за 
дней. Получаем уравнение:
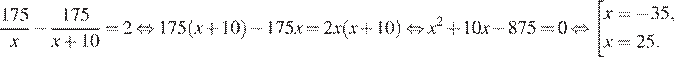
Отрицательный корень не подходит по условию задачи, следовательно, плиточник планирует ежедневно укладывать по 25 кв. м плитки.
12. Найдите наибольшее значение функции 
на отрезке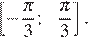 
Решение.
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
Наибольшим значением функции на заданном отрезке будет наибольшее из чисел 
и 
Найдем их:
,
Заметим, что 
, поэтому наибольшее значение функции на отрезке равно 4.
Ответ: 4.
13. а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение.
а) Найдем область определения уравнения:
Найдем корни числителя, используем формулу 
Откуда 
С учетом области определения уравнения получаем:
б) Заметим, что 
значит, из первой серии корней указанному отрезку принадлежит только 
Из неравенств 
следует, что ни один из корней второй серии не принадлежит указанному отрезку.
Ответ: а) 
б) 
14. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известны длины рёбер: AB = 4, BC = 3, AA 1 = 2. Точки P и Q — середины рёбер A 1 B 1 и CC 1 соответственно. Плоскость APQ пересекает ребро B 1 C 1 в точке U.
а) Докажите, что B 1 U: UC 1 = 2: 1.
б) Найдите площадь сечения параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью APQ.
Решение.
а) Пусть прямые AP и BB 1 пересекаются в точке X (см. рисунок). Тогда точка U — точка пересечения прямых XQ и B 1 C 1.
Треугольники AXB и PXB 1 подобны, откуда
Треугольники B 1 XU и C 1 QU подобны, откуда
Значит. 
б) Пусть Y — точка пересечения прямых QX и BC, а V — точка пересечения прямых CD и AY. Тогда пятиугольник APUQV — сечение, площадь которого надо найти.
Треугольники C 1 UQ и CYQ равны, откуда CY = C 1 U = 1.
Треугольники AYB и VYC подобны, откуда 
Четырёхугольник APUY — равнобедренная трапеция, в которой
Треугольник QYV — равносторонний состороной 
нетрудно вычислить, что его площадь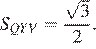 
Вычислим высоту трапеции APUY, 
Таким образом, её площадь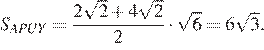 
Значит, искомая площадь равна 
Ответ: 
15. Решите неравенство 
Решение.
Найдём ОДЗ неравенства:
Применим теорему о знаке логарифма: знак 
на ОДЗ совпадает со знаком произведения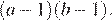 
Имеем:
С учётом ОДЗ получаем: 
или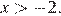 
Ответ: 
Приведём другое решение.
Заметим, что аргумент логарифма не меньше 1: 
при любых значениях х. Значит, логарифм положителен, если его основание больше 1, т. е. при 
и отрицателен, если его основание меньше 1, если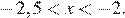 
При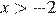 
выражение 3 x + 7 положительно, а при 
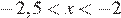исходное неравенство равносильно неравенству 
откуда 
Таким образом, решение исходного неравенства:
или