ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ЛИНИИ

СОДЕРЖАНИЕ

Введение ……………………………………………4

1. Внутренние усилия и напряжения в сечении …….5

2. Определение положения нейтральной линии…….6

3. Расчеты на прочность …………………………….. 7

4. Построения ядра сечения………………………….. 9

5. Пример расчета ……………………………………10

6. Литература …………………………………………17

7. Вопросы для самоконтроля ………………… ……18

8. Расчетно-графическая работа «Расчет жесткого бруса на внецентренное сжатие» ……………….18

Приложение № 1 …………………………………… 20

Приложение № 2 …………………………………… 24

ВВЕДЕНИЕ

Сложное сопротивление, при котором прямолиней-ный жесткий брус (рис.1) сжат или растянут силой, направленной параллельно его оси и не проходящей через центр тяжести сечения, называется внецентренном сжатием или внецентренном растяжением.

Рис.1. Схема приложения нагрузки

В том случае, когда на брус действуют несколько параллельных сил, то при расчетах будет рассматриваться их равнодействующая.

При внецентренном приложении нагрузки в попереч-ных сечениях элементов возникают продольная сила N и изгибающие моменты относительно осей y и z M_Y и M_Z.

Так как такие элементы конструкций как колонны, мостовые опоры или фундаменты сооружений обычно подвержены действию сжимающих сил, то ограничимся рассмотрением случая внецентренного сжатия.

Проанализируем, какие внутренние усилия и напряжения могут возникать в рассматриваемом нормальном поперечном сечении бруса при внецентренном сжатии.

 

 

Внутренние усилия и напряжения в сечении

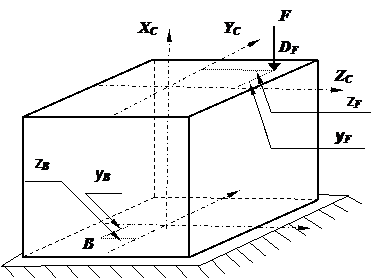На рис. 2 показана расчетная схема бруса с прямо-линейной осью х_с , к которому в точке D_F с координатами z_F и y_F приложена сжимающая сила F.

 

 

	Рис. 2. Схема приложения нагрузки к брусу

 

Оси у_с и z_c – главные центральные оси сечения (главные оси инерции). Для определения напряжение в точке В поперечного сечения, площадь которого обозна-чена символом А, необходимо знать величину и знак внутренних усилий, действующих в этом сечении. Внутренние усилия определяются по следующим формулам:

N = – F, M_Y = – F × z_F, M_Z = – F × y_F. (1)

В приведенных формулах знак изгибающего момента определяется по следующему принципу: положительный изгибающий момент должен вызывать растяжение волокон с положительными координатами в выбранной системе отсчета, а отрицательный момент должен вызывать сжатие этих волокон.

Нормальные напряжения в точке В:

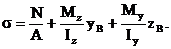(2)

В этой формуле знак внутренних усилий принимается в соответствии с (1), а координаты точки В z_В и y_В вводятся со своими знаками.

 

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ЛИНИИ

Так как нейтральная (нулевая) линия отделяет сжатую зону сечения от растянутой, то нормальные напряжения в точках, лежащих на нейтральной линии равны 0:

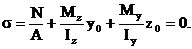(3)

Подставляя в уравнение (3) значения внутренних усилий и квадраты радиусов инерции сечения относительно главных осей вместо осевых моментов инерции, получаем следующее выражение:

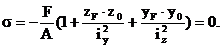(4)

В выражении (4) 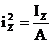, 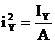– квадраты радиусов инерции сечения относительно главных центральных осей. Так как отношение F/A ¹ 0, то

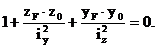(5)

Уравнение (5) – уравнение нейтральной линии, которым удобнее пользоваться, приведя его к уравнению в отрезках:

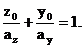(6)

Здесь a_Z и a_Y – отрезки, отсекаемые нейтральной линией на координатных осях, определяемые по формулам:

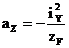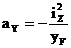, (7)

Для построения нейтральной линии рассчитываются отрезки a_z и a_y, в масштабе откладываются от начала координат и нейтральная линия проводится через концы этих отрезков. Координаты полюса z_F и y_F должны вводится в расчет с учетом правила знаков.

 

РАСЧЕТЫНА ПРОЧНОСТЬ

При внецентренном сжатии нормальные напряжения в сечении изменяются по линейному закону пропорцио-нально расстоянию от нейтральной линии. На рис. 3 пока-зан полюс (точка Б, в которой приложена сжимающая сила F) и положение нейтральной линии сечения.

 

 

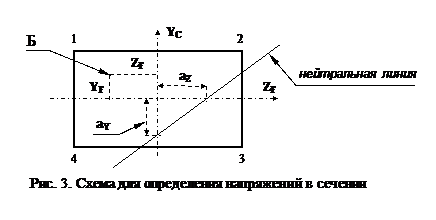
Наиболее удалены от нейтральной линии точка 1 c координатами z₁ и y₁ и точка 3, координаты которой z₃ и y₃. В этих точках возникают экстремальные напряжения: наибольшие сжимающие в т. 1, а наибольшие растягиваю-щие в т. 3. Величина напряжений в этих точках определя-ется в соответствии с (2):

.

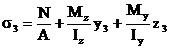Условия прочности для рассматриваемой схемы: s₁ ≤ R_сж и s₃ ≤ R_раст. Используя уравнение (4), можно записать условия прочности в следующем виде:

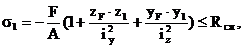(8)

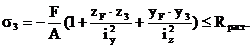(9)

В эти уравнения координаты полюса и точек, в которых определяются напряжения, подставляются с учетом их знаков.

Условия (8) и (9) позволяют решать следующие три типа задач при внецентренном приложении нагрузки:

А. Проектная задача

Задано значение силы F, расчетные сопротивления материала бруса R_сж и R_раст, координаты полюса и точек сечения, в которых действуют экстремальные напряжения. Требуется рассчитать размеры поперечного сечения. Для выполнения поставленной задачи все геометрические характеристики (А, I_Z, I_Y) выражаются через один параметр – или высоту, или ширину сечения. Из двух значений площади, вычисленной по формулам (8) и (9), за искомую следует принять большую.

Б. Определение несущей способности

Задано: расчетные сопротивления материала бруса R_сж и R_раст, геометрические характеристики сечения А, I_Z, I_Y, координаты полюса и тех точек, в которых действуют экстремальные напряжения. Требуется определить предельное значение сжимающей силы F. Из двух полученных значений силы F, за искомое принимается наименьшее.

В. Проверочная задача

Задано: геометрические характеристики сечения А, I_Z, I_Y, координаты полюса и точек, в которых действуют экстремальные напряжения, расчетные сопротивления материала бруса R_сж и R_раст, значение силы F. Требуется проверить выполнение условий (8) и (9).

 

ПОСТРОЕНИЕ ЯДРА СЕЧЕНИЯ

В зависимости от точки приложения внешней сжимающей нагрузки к брусу, нейтральная линия может пересекать сечение, касаться его или проходить вне сечения. Эти варианты показаны на рис. 4.

При внецентренном приложении нагрузки к брусу, выполненному из таких хрупких материалов, как бетон, кирпичная или бутовая кладка, возникает задача о том, как приложить сжимающую силу F, чтобы в поперечном сечении возникали только сжимающие напряжения. Решение этой задачи производится путем построения ядра сечения.

 

Ядром сечения называется очерченная вокруг центра тяжести сечения область, обладающая следующим свойством: сила F, приложенная в этой области, вызовет по всему поперечному сечению напряжения одного знака.

Контур ядра сечения строится в следующей последовательности:

- проводятся несколько касательных вокруг контура сечения, которые принимаются за нейтральные линии;

- определяются а_z и a_y – отрезки, которые нейтраль-ные линии отсекают на осях z_c и y_c;

- используя зависимости (7), определяются координа-ты характерных точек ядра сечения:

y_я = ; z_я =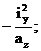

- по найденным точкам y_я и z_я строится контур ядра сечения.

ПРИМЕР РАСЧЕТА

На рис. 5 показана схема жесткого бруса и прило-женная к нему нагрузка.

Для поперечного сечения, расположенного в основании бруса, требуется: определить величину предельной силы F, приложенной в указанной точке, определить положение нейтральной линии, рассчитать напряжения в характерных точках контура, построить эпюру этих напряжений и построить ядро сечения.

Расчетные сопротивления материала бруса:

R_сж = 8 МПа, а R_раст = 2 МПа. Параметр «a» показанного на рис. 6 сечения равен 0,2м.

Последовательность расчета следующая.

1. Определение координат центра тяжести сечения

Для этого поперечное сечение сложной формы разбивается на простые фигуры, площади и положения центров тяжести которых известно. В рассматриваемом примере сечение разбито два прямоугольника и два одинаковых треугольника. Один прямоугольник площадью А₁ = 12а², второй площадью А₂ = 2а²; площадь каждого треугольника А₃ =2а².

 

 

Статический момент площади сечения относительно произвольной начальной оси Z₀:

S_Z0 = A₁×y₁ – A₂ ×y₂ + 2A₃ ×y₃

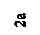
S_Z0 = 12a² × 2a – 2a² × a + 2(2a² × 8a / 3) = 32,67a³.

 

 

Расстояние у_С от оси Z₀ до оси Z_С

у_С = S_Z0 / SА_i = 32,67a³ / 14a² = 2,33a

2. Вычисление квадратов радиусов инерции

Квадраты радиусов инерции сечения рассчитываются по формулам: i_z² = I_ZC /A, i_y² = I_YC /A, где

I_ZC = I_Z1 + А₁ × b₁² – (I_Z2 + А₂ × b₂²) + 2(I_Z3 + А₃ × b₃²)

I_YC = I_Y1 – I_Y2 + 2(I_Y3 + А₃ × d₃²).

Здесь b₁ = Y_C - Y₁; b₂ = Y_C - Y₂; b₃ = Y₃ - Y_С;

d₃ = 11а /6;

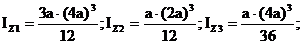
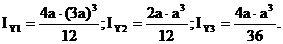
Подстановка этих значений в выражения

главных моментов инерции дает следующие

результаты:

I_ZC = 17,111а⁴; I_YC = 22,500а⁴.

Квадраты радиусов инерции сечения:

i_z² = 17,111a⁴/14a² = 1,222a² = 0,0489м²;

i_y² = 22,5a⁴/14a² = 1,607a² = 0,0643м².

3. Определение положения нейтральной линии

Координаты точки приложения сжимающей силы F (координаты полюса): z_F = - 2,5a; y_F = 1,67a

Отрезки, отсекаемые нейтральной линией на коорди-натных осях: а_z = - i_y²/z_F, а_y = - i_z²/y_F.

а_z = - i_y²/z_F = -1,607a²/(-2,5a) = 0,643a = 0,129м;

а_y = - i_z²/y_F = -1,222a²/1,67a = - 0,732a = - 0,146м.

4. Определение предельного значения

сжимающей силы

Наиболее удалены от нейтральной линии следующие точки:

- в сжатой зоне точка 1, координаты которой z₁ = - 2,5a, y₁ = 1,67a;

- в растянутой зоне – точка 3 с координатами z₃ =1,5a, y₃ = - 2,33a.

 

YC

 

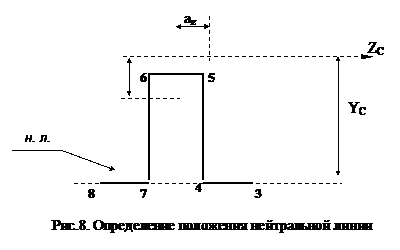Для этих точек должны соблюдаться условия прочности – напряжения в них не должны превышать расчетных сопротивлений материала:

 

(*)

(**)

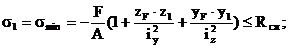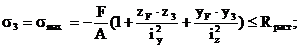Из выражения (*) предельная величина сжимающей силы F_пр, приложенной в т.1:

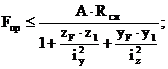
Подставляя числовые значения величин, входящих в это неравенство (с учетом знака R_сж), получим: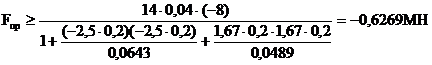

Из выражения (**) вычисляется значение F_пр:

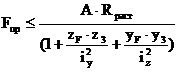
Из этих двух полученных значений F_пр за расчетное принимается наименьшее (по модулю) F_пр = 0,218 МН.

5. Определение напряжений в сечении бруса

Нормальные напряжения в произвольной точке сечения определяются по формуле:

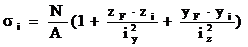(10)

Подставляя в эту формулу значения N = (–)F_пр и координаты характерных контурных точек, вычисляют действующие в них напряжения.

В табл.1 показаны координаты характерных точек сечения и даны результаты выполненных расчетов по определению напряжений в этих точках.

Для построения эпюры, показывающей распределение нормальных напряжений по поперечному сечению бруса, сечение удобно показывать в изометрической проекции. Эпюра s приведена на рис. 9.

 

 

Таблица 1

№ точек контура	Координаты точек	Напряжения s, МПа
zi	yi
	-2,5а (-0,5м)	1,67а (0,334м)	- 3,18
	2,5а (0,5м)	1,67а (0,334м)	+ 0,27
	1,5а (0,3м)	-2,33а (-0,466м)	+ 2,00
	0,5а (0,1м)	-2,33а (-0,466м)	+ 1,31
	0,5а (0,1м)	-0,33а (-0,066м)	+ 0,10
	-0,5а (-0,1м)	-0,33а (-0,066м)	- 0,59
	-0,5а (-0,1м)	-2,33а (-0,466м)	+ 0,62
	-1,5а (-0,3м)	-2,33а (-0,466м)	- 0,07

6. Построение ядра сечения

Для построения ядра сечения проводятся четыре касательные к контуру сечения, которые рассматриваются как нулевые линии и определяются отрезки, отсекаемые касательными (нулевыми линиями) на главных центральных осях инерции.

Касательная I-I: a_z = ¥, a_y =1,67a

Касательная II-II: a_z = ¥, a_y = -2,33a

Касательная III-III: a_z =1,58а, a_y = -8,33a

Касательная IV-IV: a_z = -1,58а, a_y = -8,33a

Зная величину отрезков, отсекаемых нулевыми линиями на координатных осях, определяются координаты ядра сечения:

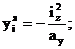
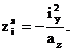
На рис.8 показаны нулевые линии и построено ядро сечения.

 

 

 

Результаты определения характерных точек ядра сечения обычно выполняются в табличном виде. Итоги выполненных расчетов приводятся в табл. 2, в которой даны координаты характерных точек ядра сечения.

Соединяя точки ядра 1-3-2-4 прямыми линиями, получаем контур ядра сечения.

Таблица 2

Нулевая линия	Отрезки, отсекаемые на координатных осях	№ точек ядра	Координаты точек ядра
аz	аy	yя	zя
I-I	¥	1,67a (0,334см)		- 0,73а (- 0,146м)
II-II	¥	-2,33а (-0,466м)		0,52а (0,105м)
III-III	2,08а (0,416м)	-8,33а (-1,666м)		0,15а (0,029м)	-0,77а (-0,155м)
IV-IV	-2,08а (-0,416м)	-8,33а (-1,666м)		0,15а (0,029м)	0,77а (0,155м)

 

ЛИТЕРАТУРА

1.Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов.– 2-е изд. – М.: Высш. шк., 2001. -560с.

2. Сопротивление материалов с основами теории упру-гости и пластичности: Учеб. для вузов под ред. Г.С. Варда-няна. – М.: Изд-во АСВ, 1995. -568с.

3. Павлов П.А., Паршин Л.К., Мельников Б.Е., Шерсте-нев И.А. Сопротивление материалов: Учеб. пособ./под ред. Б.Е. Мельникова – СПб.: Изд-во «Лань», 2003. -528с.

4. Сопротивление материалов: Руководство для реше-ния задач и выполнения лабораторных и расчетно-графических работ / В.А. Копнов, С.Н. Кривошапко. – М.: Высш. шк., 2003. – 351с.

ВОПРОСЫДЛЯ САМОКОНТРОЛЯ

1. Как определяются внутренние усилия в сечениях жесткого бруса при внецентренном действии нагрузки?

2. Как определяется положение нейтральной (нулевой) линии при внецентренном сжатии или растяжении?

3. Указать, какой из перечисленных факторов повлияет на положение нейтральной линии:

- изменение величины приложенной внешней силы;

- изменение точки приложения этой силы;

- изменениие знака приложенной внешней силы.

4. Как определяется напряжение в заданной точке сечения при внецентренном действии нагрузки?

5. Что называется ядром сечения? Как строится ядро?

6. Какие типы задач позволяет решить условие прочнос-ти при внецентренном приложении нагрузки?