Понятие "производная" является фундаментальным для более сложных разделов высшей математики, математического анализ, дифференциального исчисления и т.д.
Поэтому без четкого понимания этого математического термина невозможно дальнейшее освоение математики.
Кроме того, производная используется при решении практических задач, связанных с исследованием физических явлений и построением графиков функций.
В средней школе учащиеся испытывают затруднения при изучении производной. Это связано с:
1) Производная является одним из абстрактных понятий, физический смысл которой трудно представить наглядно;
2) Определение производной базируется напонятий предела, которому уделяется недостаточно внимания в школьном курсе;
3) При определении производной используются новые термины: предел отношения, приращение аргумента, функции и т.д.
Поэтому изложение ведется на наглядно-интуитивной основе, без доказательств многих формул, только лишь с пояснениями.
Александр Григорьевич Мордкович советует использовать как можно меньше схоластики (рассуждений ни о чем), меньше жестких моделей (научных терминов), меньше опираться на левое полушарие; больше использовать иллюстраций, правдоподобных рассуждений, мягких моделей (примеров из жизни).
Приступая к изучению производной целесообразно:
1) повторить все вопросы, связанные с линейными и элементарными функциями, тк.к. основная идея дифференциального исчисления - это представление функции как о линейной в достаточно малой окрестности некоторой точки;
2) отработать такие понятия, как приращение функции и аргумента, выработать твердые навыки их нахождения;
3) выяснить геометрический смысл отношения приращения функции к приращению аргумента, ввести понятие касательной к кривой как предельное положение секущей.
Классически удачным способом введения понятия производной является решение подводящих задач о нахождении мгновенной скорости прямолинейного движения, о линейной плотности в точке, о мгновенной величине тока и т.д.
Главная цель на этом этапе - показать учащимся целесообразность изучения этой темы.
На основе уже имеющихся знаний о пределе функции в точке формулируется определение производной как предела отношения приращения функции к приращению аргумента. Наилучший вариант - сделать это на геометрической основе, что позволит еще раз показать идею линеаризации (изучения кривой к изучению ломаной, далее - к изучению отрезков, являющихся хордами, содержащими 2 точки кривой).
Особое внимание необходимо уделить сложной функции и ее производной, т.к. наибольшее количество ошибок связано именно с ней.
Вступительная беседа к геометрическому смыслу производной может иметь следующую идею:
1) Показать, что функции, графиками которых являются кривые, описывают многие важные физические и технические процессы;
2) По сравнению с прямой кривые постоянно меняют наклон: возрастание - на убывание и наоборот;
3) Могут существовать значения у, которым соответствует несколько значений х.
Этапы изучения геометрического смысла:
1. Определение углового коэффициента прямой, угла наклона между положительным направлением оси ОХ и прямой, свойства функции и графика в зависимости от коэффициента.
2. Определение касательной к графику дифференцируемой функции.
3. Геометрический смысл производной.
4. Уравнение касательной к графику дифференцируемой функции.
Следующим разделом темы является применение производной к решению задач.
Содержание этого раздела: применение производной в геометрии и физике, приближенных вычислениях, исследованиях функции, построении графиков с помощью производной и решение задач на нахождение наибольшего и наименьшего значения функции.
Теоретический материал по исследованию функции может быть введен следующим образом:
1. Сформулировать все утверждения, оставить без доказательств.
2. Показать схему доказательства теорем.
3. Формулу Лагранжа дать без доказательства, а остальные теоремы - доказать на ее основе.
Основные этапы исследования функции:
1. ООФ.
2. Нахождение производной.
3. Нахождение стационарных точек.
4. Промежутки монотонности.
5. Точки экстремума.
6. Построение графика функции.
Еще одним трудным вопросом является решение задач на наибольшее и наименьшее значение (задачи на оптимизацию), связаны с построением и исследованием некоторой модели.
Трудности возникают при составлении функции на основе условия задачи. Здесь требуется грамотный анализ условия, опора на полученный при работе с сюжетными (текстовыми) задачами опыт поиска решения.
1. Образовательные цели изучения производной функции
При изучении темы "Производная" проявляются известные трудности, связанные с осуществлением предельных переходов. Важно поэтому придать изложению возможно более наглядный и конкретный характер.
Включённые в курс сведения о пределах имеют вспомогательный характер, они не обходимы для вывода формул производных. Основное внимание должно быть уделено не формальному применению теорем о пределах, а сознательному проведению предельных переходов для приближённого вычисления значений конкретных функций и их приращений. Многочлены невысоких степеней и их частных -наиболее простой объект для иллюстрации идеи предельного перехода.
Определению производной функции как предела разностного отношения предшествует рассмотрению особенностей поведения графиков гладких функций, приводящее к понятию касательной. Производная функции появляется сначала как тангенс угла наклона касательной к оси абсцисс. Тем самым с понятием производной на первом этапе связывается наглядный образ – касательная. Предельные переходы появляются как средство вычисления производной.
При изучении применения производной существенная роль отводится наглядным представлениям о производной. Опора на геометрический и механический смысл делают интуитивно ясными критерии возрастания и убывания функций, признаки максимума минимума.
Решение тестовых задач физического, геометрического и практического содержания с применением производной позволяет учащимся ознакомиться со всеми этапами решения прикладных задач: составление математической модели (перевод задачи на язык функций), решение полученной задачи средствами математического анализа, и наконец, интерпретация полученного решения в терминах исходной задачи.
2. Различные подходы к введению понятия производной функции в курсе средней школы
Различные подходы к введению производной определяются логической связью этого понятия с более общим понятием предела функции в точке.
Логический подход при введении производной в качестве базисного понятия использует определение предела функции в точке. Так в учебных программах по математике 1968 года, используя этот подход, определяли это понятие: 1) исходя из арифметического толкования предела функции (определение по Коши или на языке абсолютной погрешности):
2) исходя из операции предела функции в точке через окрестности (топологическое): 
a- предельная точка множества E, т.е.
В действующих школьных программах по математике при введении производной функции используют исторический подход, т.е. первоначально формируются понятия производной, и только затем, как обобщение, понятие предела функции. При таком подходе большое внимание уделяется практическим аспектам изучения производной.
3. Методическая схема изучения производной
I. Привести подводящую задачу, раскрывающую физический смысл понятия производной: свободное падение тела, которое не является равномерным. Охарактеризуем скорость падения в каждый данный момент времени t, т.е. введём понятие мгновенной скорости свободного падения тела. Известно, что средняя скорость определяется отношением 
, причём чем меньше значение 
, тем менее "заметно" изменение средней скорости падения. При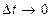 
, отношение 
стремится к значению мгновенной скорости. Таким образом мгновенная скорость характеризует скорость изменения пути 
в момент времени t.
В общем случае, с любым реальным процессом может быть связана задача:
Пусть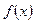 
-параметр данного процесса, зависимости от x; найти скорость изменения параметра 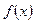в момент, когда 
. Решение задачи сводится к нахождению отношения приращения параметра 
, соответствующую приращению 
.
II. Сформулировать определение понятия производной.
Так как в определении отсутствует понятие предела, то первоначально следует сформировать у учащихся понятие приращения как изменения и аргумента и функции.
Например:
После рассмотрения геометрического смысла производной вводим определение:
Производной функции в точке 
называется число, к которому стремится разностное отношение:
Полезен небольшой анализ формулировки определения, позволяющий чётче выделить признаки данного понятия: 1) число, 2) к которому стремится разностное отношение 
3) при 
Закреплению определения производной способствует вопрос: "Как найти производную функции 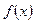в точке ?", ответ на который может быть дан в форме алгоритма: 1) значению придаём приращение 
; 2) находим приращение функции 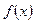в точке 
; 3) составляем разностное соотношение; 4) находим число 
(если такое число существует), к которому стремится при
III. Конкретизировать понятие производной (путём вычисления производной по определению: выяснение её геометрического смысла, графическое отыскание производной)
Первый пример на выяснение производной полезно выполнить на двух уровнях: а) задано конкретным числом; б) берётся в общем виде.
Например: Дана функция 
. Найти её производную в точке: а) x=2; б)
а) Придадим приращение в точке х=2, новое (приращённое) значение аргумента –(2+ ). Найдём приращение функции:
Вычислим разность отношения
Оно стремится к 2 при 
б) 
, приращённое значение аргумента: +
.
Составим разностные отношение: 
, которые при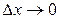 
стремится к числу 
.
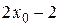Для конкретизации понятия производной может быть использован графический метод, суть которого в следующем:
1) На примере функции покажите, что разностное отношение 
есть функция с аргументом 
. Охарактеризуйте эту функцию. Обратимся к рассмотренному примеру:
, 
, 
Наша функция возрастающая, т.е. если
2) Постройте график функции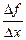 
и с его помощью покажите число, к которому стремится отношение при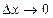 
. Пусть
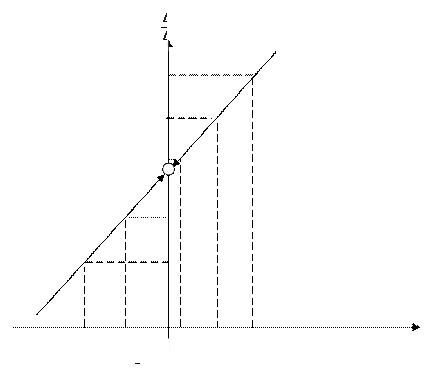
3) Мотивировать необходимость теорем о вычислении производной, сформулировать и доказать эти теоремы.
4) Рассмотреть приложение производной.