При изучении кибернетических и интеллектуальных систем на первое место выдвигаются языковые и логические конструкции. Математическая логика изучает базовые понятия синтаксиса (формы) и семантики (содержания) естественного языка. Математическая логика содержит три крупных направления исследований – логика высказываний, логика предикатов, теория доказательств.
Рассмотрим простейшие конструкции естественного языка, повествовательные предложения и тексты, составленные из них, - так называемые высказывания.
Высказыванием называется повествовательное предложение (текст) естественного языка, о котором имеет смысл говорить истинно оно или ложно.
Например, «студент Петров присутствует на лекции», «эта стена белая», «33 =28» и т.д.
Заметим, что предложение «Город x стоит на реке y » не является высказыванием, пока не заданы x и y, так как здесь нельзя определить истина это или ложь.
Из данных высказываний можно составить новые, сложные высказывания с помощью так называемых логических операций. Истинность значений сложных высказываний определяется только истинностью значений составляющих высказываний, а не их смыслом. Простейшие высказывания, в которых не выделяются части, являющиеся высказываниями, будем обозначать прописными латинскими буквами A, B, C, … и называть атомарными. В математической логике истинность или ложность сложных высказываний, образованных при помощи логических связок, устанавливается независимо от смысла простых высказываний, составляющих сложное высказывание. Истинность или ложность сложного высказывания полностью определяется, во-первых, тем, какие логические связки использованы для образования сложного высказывания, и, во-вторых, тем, какие из простых высказываний, образующих сложное высказывание, истинны и какие ложны. Для этого в логике вводятся операции над высказываниями, соответствующие связкам, при помощи которых образуются сложные высказывания. Тем самым, союзам «и», «или», словам «тогда и только тогда …», «если …, то …» придаётся точный однозначный смысл.
|
|
Если высказывание образовано из двух высказываний при помощи союза «или », то говорят, что оно является суммой (дизъюнкцией) этих высказываний. Сумму любых высказываний А и В записывают в виде A  B
B  .
.
Определение: Дизъюнкцией двух высказываний А и В называется высказывание ложное тогда и только тогда, когда ложны оба эти высказывания.
Таблица 1

| 
| 
|
| И | И | |
| И | Л | |
| Л | И | |
| Л | Л |
Буква И означает, что соответствующее высказывание истинно, Л – соответствующее высказывание ложно.
Высказывание, составленное из двух высказываний при помощи союза «и », называют произведением (конъюнкцией) этих высказываний. Произведение любых высказываний А и В записывают в виде A  B
B  .
.
Определение: Конъюнкцией двух высказываний А и В называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.
Таблица 2

| 
| 
|
| И | И | |
| И | Л | |
| Л | И | |
| Л | Л |
Высказывание, образованное из двух высказываний при помощи слов «тогда и только тогда, когда … », называют эквивалентностью. Для эквивалентности используют знак  (или
(или  ), т.е. пишут А
), т.е. пишут А  В (или
В (или  ).
).
Определение: Эквивалентность А  В представляет собой ложное высказывание, если одно из высказываний истинно, а другое ложно.
В представляет собой ложное высказывание, если одно из высказываний истинно, а другое ложно.
|
|
Таблица 3

| 
|   
|
| И | И | |
| И | Л | |
| Л | И | |
| Л | Л |
Высказывания, образованные из двух высказываний при помощи слов «если …, то … », называют импликацией. Для импликации используют знак  , т.е. пишут А
, т.е. пишут А  В (читается: «из А следует В » или «если А, то В »).
В (читается: «из А следует В » или «если А, то В »).
Определение: Импликация А  В есть ложное высказывание только в том случае, если А – истинно, а В – ложно.
В есть ложное высказывание только в том случае, если А – истинно, а В – ложно.
Таблица 4

| 
| A  B B
|
| И | И | |
| И | Л | |
| Л | И | |
| Л | Л |
Помимо только что рассмотренных четырёх логических операций в математике используется ещё одна простая, но очень важная операция – операция отрицания. Эта операция соответствует логической связке «не». Каждому высказыванию А можно сопоставить утверждение, заключающееся в том, что высказывание А ложно. Такое утверждение либо истинно, либо ложно и, следовательно, само является высказыванием, причём истинным, если А ложно, и ложным, если А истинно. Это новое высказывание обозначают через
 и называют отрицанием А.
и называют отрицанием А.
Таблица 5

| 
|
| И | |
| Л |
Итак, истинность или ложность высказывания, образованного из каких-либо высказываний с помощью операций сложения, умножения, эквивалентности и импликации, зависит только от распределения истинности или ложности между высказываниями, над которыми производятся логические операции. Эту зависимость удобно описывать следующей таблицей, которая называется таблицей истинности логических операции:
|
|

| 
| 
| 
|   
| A  B B
| 
|
| И | И | И | И | И | И | Л |
| И | Л | И | Л | Л | Л | - |
| Л | И | И | Л | Л | И | И |
| Л | Л | Л | Л | И | И | - |
Для дальнейшего изложения из всех рассмотренных логических операций особенно важной является импликация A  B. Первый член импликации A
B. Первый член импликации A  B высказывание А называется посылкой или условием, второй член В – заключением. Таблица истинности для импликации, в отличии от таблиц 1…3, изменяется при перестановке столбцов для А и В. Отметим также, что импликация не полностью соответствует обычному пониманию слов «если …, то …» и «следует». Из третьей и четвёртой строк таблицы 4 вытекает, что если А ложно, то, каково бы ни было В, высказывание A
B высказывание А называется посылкой или условием, второй член В – заключением. Таблица истинности для импликации, в отличии от таблиц 1…3, изменяется при перестановке столбцов для А и В. Отметим также, что импликация не полностью соответствует обычному пониманию слов «если …, то …» и «следует». Из третьей и четвёртой строк таблицы 4 вытекает, что если А ложно, то, каково бы ни было В, высказывание A  B считается истинным. Таким образом, из неверного утверждения следует всё что угодно. Например, утверждения «если 6 простое число, то 7 < 6 » или «если 7<6, то существуют ведьмы » являются истинными.
B считается истинным. Таким образом, из неверного утверждения следует всё что угодно. Например, утверждения «если 6 простое число, то 7 < 6 » или «если 7<6, то существуют ведьмы » являются истинными.
Договорились считать, что сильнее всех связывает знак отрицания, за ним следуют знаки конъюнкции, дизъюнкции и импликации, слабее всех связывает знак эквиваленции.
Пример 14. Доказать, что 
| А | В | |||||
| И | И | |||||
| И | Л | |||||
| Л | И | |||||
| Л | Л |
Легко проверяются следующие равносильности:
1. 
2. 
3. 
4. A(BC)=(AB)C
5. 
6. 
7. 
8. 
9. 
10. 
11. 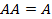
12. 
13. 
14.  =I,
=I,  =L,
=L,  ,
,  ,
,  ,
,  ,
,
где I – тождественно истинное высказывание, L – тождественно ложное высказывание.
Использованная литература:
Виленкин Н.Я., Комбинаторика. –М.: Издательство «Наука», 1969. -328 с.
Киселёв А.П., Алгебра: учебник для школы, ч.2. –М.: Просвещение, 1965. -230 с.
Егерев В.К. и др., Сборник задач по математике под редакцией М. И. Сканави. –М.: Высшая школа, 1998. -528 с.
Бачурин В.А., Сборник задач по математике. –М.: Высшая школа, 2003. -560 с.
Кутасов А.Д. и др., Пособие по математике для поступающих в вузы. –М.: Наука, 1982. -480 с.
Виленкин Н.Я. и др., Математика. –М.: Просвещение, 1977. -350 с.