Функция распределения вероятностей случайной величины
Функцией распределения называют функцию F(х), определяющую вероятность того, что непрерывная случайная величина Х в результате испытания примет значение, меньшее числа х:
 .
.
Свойства функции распределения:
1) значения функции распределения принадлежат отрезку [0,1]: 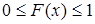 ;
;
2) F(x) – неубывающая функция, т.е.  если
если  ;
;
3) вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:  ;
;
4) если все возможные значения случайной величины принадлежат интервалу (a, b), то  при
при  и
и  при
при  .
.
Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
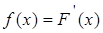 .
.
Свойства плотности распределения:
1) плотность распределения – неотрицательная функция: f(x)≥0;
2) несобственный интеграл от плотности распределения в пределах от –∞ до +∞ равен единице:  ;
;
3) вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (х1; х2), равна определенному интегралу от плотности распределения, взятому от a до b:
 . (1)
. (1)
Полученный результат геометрически отражает тот факт, что вероятность попадания непрерывной случайной величины в заданный интервал (х1; х2) равна площади криволинейной трапеции, ограниченной осью Ох, графиком плотности распределения f(x) и прямыми  и
и  .
.
1.2. Числовые характеристики случайных величин
Математическое ожидание М(Х) непрерывной случайной величины, распределенной на интервале (х1; х2), характеризует ее среднее значение и определяется по формуле
 (2)
(2)
Дисперсия D(X) непрерывной случайной величины, распределенной на интервале (х1; х2), характеризует ее рассеяние относительно математического ожидания и определяется по формуле
 . (3)
. (3)
Если возможные значения непрерывной случайной величины принадлежат всей числовой оси Ох, то математическое ожидание и дисперсия определяются по формулам
 и
и  .
.
Среднее квадратическое отклонение σ(Х) случайной непрерывной величины определяется по формуле
 . (4)
. (4)
Начальным моментом  порядка s случайной величины Х называют математическое ожидание величины Хs:
порядка s случайной величины Х называют математическое ожидание величины Хs:
 . (5)
. (5)
Начальный момент первого порядка случайной величины Х соответствует ее математическому ожиданию.
Центральным моментом  порядка s случайной величины Х называют математическое ожидание величины
порядка s случайной величины Х называют математическое ожидание величины  :
:
 . (6)
. (6)
Центральные и начальные моменты случайной величины Х связаны следующими соотношениями:
1)  ;
;
2)  ;
;
3)  .
.
Центральный момент третьего порядка  случайной величины Х характеризует асимметрию (скошенность) распределения и служит для вычисления коэффициента асимметрии
случайной величины Х характеризует асимметрию (скошенность) распределения и служит для вычисления коэффициента асимметрии  , который определяется по формуле
, который определяется по формуле
 . (7)
. (7)
Асимметрия положительна, если «длинная часть» кривой плотности распределения расположена справа от математического ожидания. Асимметрия отрицательна, если «длинная часть» кривой распределения расположена слева от математического ожидания.
Центральный момент четвертого порядка  случайной величины Х характеризует «крутость» или островершинность графика ее плотности распределения и служит для вычисления эксцесса
случайной величины Х характеризует «крутость» или островершинность графика ее плотности распределения и служит для вычисления эксцесса  , который определяется по формуле
, который определяется по формуле
 . (8)
. (8)
Эксцесс положительный, если кривая распределения имеет острую вершину. Эксцесс отрицательный, если кривая распределения имеет пологую вершину.
Равномерное распределение вероятностей
Распределение вероятностей называют равномерным, если на интервале (a; b), которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:
 (9)
(9)
Функция равномерного распределения на интервале (a; b) имеет вид:

Характеристики равномерного распределения определяются по формулам (2) – (4), (7), (8):
1) математическое ожидание  ;
;
2) дисперсия  ;
;
3) среднее квадратическое отклонение  ;
;
4) асимметрия  ;
;
5) эксцесс  .
.
Вероятность попадания случайной величины Х, распределенной по равномерному закону, в заданный интервал (х1; х2) определяется по формуле (1)
 .
.
Показательное распределение
Показательным (экспоненциальным) называют распределение непрерывной случайной величины Х, которое описывается плотностью
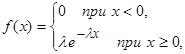 (10)
(10)
где λ – постоянная положительная величина.
Функция показательного распределения имеет вид:

Характеристики показательного распределения определяются по формулам (2) – (4):
1) математическое ожидание  ;
;
2) дисперсия  ;
;
3) среднее квадратическое отклонение  .
.
Вероятность попадания случайной величины Х, распределенной по показательному закону, в заданный интервал (х1; х2) определяется по формуле (1)
 . (11)
. (11)
Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
 (12)
(12)
Математическое ожидание нормального распределения равно параметру а. Среднее квадратическое отклонение нормального распределения равно параметру σ. Коэффициент асимметрии  и эксцесс
и эксцесс  нормального распределения равны нулю:
нормального распределения равны нулю:  и
и  .
.
Вероятность попадания нормально распределенной случайной величины Х в заданный интервал (х1; х2) определяется по формуле (1):
 , (13)
, (13)
где Ф(х) – функция Лапласа,
 . (14)
. (14)