Радиальная (круговая) СКП обсервованного места судна

Графическое счисление координат судна с учетом течения

При плавании в районе с течением, на судно действуют две силы

1.→ сила действия собственных движителей;

2.→ сила воздействия течения.

Под действием собственных движителей судно перемещается относительно воды по линии истинного курса (ИК) с относительной скоростью V₀.

Под воздействием течения судно перемещается относительно поверхности Земли по направлению течения К_t с переносной скоростью, равной скорости течения υТ.

Суммарное же (результирующее) перемещение судна относительно поверхности Земли складывается из относительного и переносного перемещений и происходит с путевой скоростью V.

Для геометрического сложения векторов по формуле необходимо на навигационной карте:

1.→ из счислимой точки начала учета течения (т. О) проложить линию истинного курса (ИК);

2.→ от т. О по линии ИК отложить (в масштабе карты) вектор скорости судна ;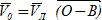

3.→ из конца вектора 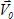(т. В) проложить линию по направлению течения (К_t) и на ней (от т. В) отложить (в том же масштабе) вектор скорости течения ;

4.→ соединить начало вектора скорости судна 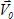(т. О) с концом вектора скорости течения (т. А)

– получим вектор путевой скорости судна – .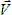

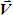Треугольник ОАВ, сторонами которого являются векторы относительной (), переносной () и путевой () скоростей, называется навигационным скоростным треугольником.

Линия, по которой перемещается центр массы судна относительно дна моря называется

линией пути судна при течении (О–А).

Путь судна при течении (ПУ_t или ПУ_β) → направление перемещения центра массы судна, измеряемое горизонтальным углом между северной частью истинного меридиана и линией пути при течении (от 0° до 360° – по часовой стрелке).

Угол сноса (β) → угол между линией истинного курса и линией пути судна, обусловленный влиянием течения (измеряется в сторону правого или левого борта от 0° до 180° со знаком «плюс» (+) или «минус» (–) соответственно.

Путь судна при течении (ПУβ), истинный курс (ИК) и угол сноса (β) связаны соотношением:

Формулы алгебраические. При вычислениях углу сноса β придается знак «плюс» (+) или «минус»(–):

•«+» → если течение действует в л/б судна, т.е. ПУβ > ИК (сносит вправо) –

•«–»→ если течение действует в пр/б судна, т.е. ПУβ < ИК (сносит влево) –

Знак угла сноса судна течением

Учет течения при графическом счислении пути судна

Графическое счисление с учетом течения ведется на навигационной карте с соблюдением некоторых правил:

1.→ линия истинного курса (ИК) и линия направления течения (К_t) проводятся с более слабым нажимом карандаша, чем линия пути при течении (ПУ_β);

2.→ вдоль линии пути при течении (ПУ_β) с внешней стороны навигационного скоростного треугольника подписывается

3.→ для каждого счислимого места строится навигационный треугольник перемещений

(Δ ОДС), подобный навигационному скоростному треугольнику (Δ ОАБ);

4.→счислимое место судна находится на его линии пути при течении (ПУ_β), около которого пишется ;

5.→ судовой журнал заполняется в соответствии с правилами его ведения.

Радиальная (круговая) СКП обсервованного места судна

Рис. 18.10. Погрешность обсервованного места судна

Поскольку обсервованное место судна образуется пересечением минимум двух линий положения а, значит, и двух полос, то на путевой карте мы получим не точку С,а так называемую фигуру погрешностей «абсд».

Размеры этой фигуры при неизменных m_ЛП будут зависеть, прежде всего, от угла пересечения линий положения – угла q.

При θq = 90° площадь фигуры погрешностей наименьшая, а при m_ЛП1 = m_ЛП2 – квадрат. Но, чем меньше будет этот θq, тем больше будет площадь фигуры погрешностей «абсд».

Вероятность нахождения обсервованного места судна в этой фигуре погрешностей равна произведению вероятностей нахождения места судна в каждой из полос, …
то есть: Р = 0,68 × 0,68 » 0,46 (46%).

Однако, точность места судна принято оценивать не параллелограммом «абсд» (ромбом, квадратом) погрешностей, а эллипсом, вписанным в этот параллелограмм.

Эллиптическая погрешность обсервованного места судна

Эллипс погрешностей обладает следующими свойствами:

1. Размеры и ориентировка эллипса погрешностей дают наглядное представление о точности определения места по различным направлениям.

2. Вероятность того, что случайная погрешность не выйдет за пределы эллипса погрешностей больше, чем для любой другой фигуры погрешности, имеющей такую же площадь.

3. Среди всех фигур, в пределах которых, вероятность нахождения судна одинакова, эллипс погрешностей имеет наименьшую площадь.

Вероятность нахождения места судна в эллипсе погрешностей равна Р = 0,39(39%).

Но эллипс погрешностей, из-за сложности его построения, применяют только при решении специальных задач судовождения.

В повседневной практике используют более грубую, но более простую оценку точности места судна – через радиальную (круговую) СКП – М₀.

Радиальная (круговая) СКП обсервованного места (М₀) построена на полуосях эллипса погрешностей (рис. 18.12).

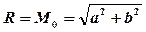
Вероятность нахождения обсервованного места судна в круге радиусом R = M₀ зависит от соотношения полуосей эллипса погрешностей.

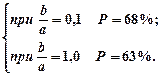
Радиальная (круговая) СКП места судна

В общем случае, вероятность нахождения места судна в круге радиусом

R = M₀ принимается равной 63% (0,63), так как в большинстве случаев соотношение полуосей эллипса b/a близко к 1.

Как видно из рис. при q = 90°(sin q = 1) полуоси эллипса погрешностей численно равны по своей величине СКП линий положения (а = m_ЛП1, b = m_ЛП2 ) и формулу (18.18) для этого случая можно записать как:

Для общего же случая (когда q ¹ 90° и sin q <1) радиальная (круговая) СКП обсервованного места судна M₀ в зависимости от СКП линий положения (m_ЛП1 и m_ЛП2) и угла их пересечения q определяется по общей формуле