Полная механическая энергия, т.е. сумма потенциальной и кинетической энергии тела, остается постоянной, если действуют только силы упругости и тяготения и отсутствуют силы трения.
Применимость закона сохранения механической энергии:
Закон сохранения механической энергии является следствием однородности времени. Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент эти условия созданы.
Закон сохранения полной механической энергии предполагает взаимное превращение кинетической энергии в потенциальную энергию и обратно в равных количествах. При этом полная энергия остается неизменной.
Справедливость закона сохранения энергии подтверждается экспериментально с высокой степенью точности.
С помощью закона сохранения механической энергии значительно проще находить кинематические величины, чем при непосредственном применении законов движения и законов динамики Ньютона.
2) Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяется. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v 1 и v 2. На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в интервале от  до
до  , от
, от  до
до  и от
и от 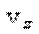 до
до  , определяются функцией распределения Максвелла
, определяются функцией распределения Максвелла

где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, что число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид


Распределение Максвелла достигает максимума при скорости 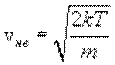 (наиболее вероятная скорость), т.е. такой скорости, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.
(наиболее вероятная скорость), т.е. такой скорости, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.
Кривая распределения Максвелла позволит найти среднюю арифметическую скорость
 .(средняя арифметическая скорость)
.(средняя арифметическая скорость)
Таким образом,

| (11.1) |
(наиболее вероятная, средняя арифметическая, средняя квадратичная)
С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.
3) 
4)


5) Гравитационная потенциальная энергия (U) системы масс (m1 и M2) на дистанции r при использовании гравитационной постоянной G равняется: 
Гравитационная энергия отображает собою потенциальную, связанную с силой гравитации, потому что необходимо преодолеть земное притяжение, чтобы выполнить работу над поднятием предметов. Если объект падает от одной точки к другой внутри гравитационного поля, то сила тяжести выполнит положительную работу, а гравитационная потенциальная энергия уменьшится на ту же величину. На гравитационную потенциальную энергию влияют высота относительно конкретной точки, масса и сила гравитационного поля. Значит потенциальная энергия больше на большем расстоянии от Земли, чем вблизи поверхности Земли
6) p=nkT
Т.к. n по условию задачи постоянная, а k является постоянной Больцмана и равна 1,38 x 10–23 Дж/К. Значит давление в данных условия будет зависеть от температуры, которая может изменяться => давление изменяется.
7)

8) В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением
|
Первый закон термодинамики для изобарного процесса дает:
|
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T 2 < T 1; внутренняя энергия убывает, Δ U < 0.
Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими.
В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид
|
т. е. газ совершает работу за счет убыли его внутренней энергии.
На плоскости (p, V) процесс адиабатического расширения (или сжатия) газа изображается кривой, которая называется адиабатой. При адиабатическом расширении газ совершает положительную работу (A > 0); поэтому его внутренняя энергия уменьшается (Δ U < 0). Это приводит к понижению температуры газа. Вследствие этого давление газа при адиабатическом расширении убывает быстрее, чем при изотермическом.
9) Энергия механической системы меняется в процессе силового воздействия смещения тел. Для характеристики этого процесса выводится понятие работы силы

10)
