Вариант № база.
1. Найдите значение выражения (3,9 − 2,4) · 8,2.
Решение.
Найдём значение выражения:
2. Найдите значение выражения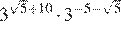 
.
Решение.
Выполним преобразования:
.
Ответ: 243.
3. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 10 000 рублей?
Решение.
Розничная цена учебника составляет 120% от оптовой цены. Чтобы найти 100% цены разделим 180 на 1,2:
.
Поскольку
,
по оптовой цене на 10 000 рублей можно купить 66 учебников.
Ответ: 66.
4. Если 
и 
— простые числа, то сумма всех делителей числа 
равна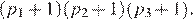 
Найдите сумму делителей числа 114.
Решение.
Разложим число 114 на простые множители: 114 = 2 · 3 · 19. Следовательно, сумма всех делителей числа 114 равна (2 + 1)(3 + 1)(19 + 1) = 3 · 4 · 20 = 240.
Ответ: 240.
5. Найдите значение выражения 
.
Решение.
Найдём значение выражения:
Ответ: 42.
6. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?
Решение.
За 4 недели в офисе расходуется 1200 · 4 = 4800 листов бумаги. Разделим 4800 на 500:
Значит, нужно купить не меньше 10 пачек бумаги.
Ответ: 10.
7. Найдите корень уравнения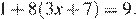 
Решение.
Последовательно получим:
Ответ: −2.
8. 
Колесо имеет 5 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
Решение.
Спицы делят колесо на пять равных секторов, а значит, делят полный угол 360° на 5 равных углов по 72° каждый.
Примечание.
В действительности, спицы не всегда делят колесо на равновеликие сектора.
Ответ: 72.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
|
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ | |
| А) масса куриного яйца Б) масса детской коляски В) масса взрослого бегемота Г) масса активного вещества в таблетке | 1) 2,5 мг 2) 14 кг 3) 50 г 4) 3 т |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
| A | Б | В | Г |
Решение.
От легкого к тяжелому: таблетка (Г - 1), яйцо (А - 3), коляска (Б - 2) и бегемот (В - 4). Окончательно получим 3241.
Ответ: 3241.
10. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение.
Всего в соревнованиях принимает участие 4 + 7 + 9 + 5 = 25 спортсменов. Значит, вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна
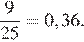
Ответ: 0,36.
11. На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах. 
Решение.
Из диаграммы видно, что число стран, в которых средний балл по математике ниже чем в Нидерландах равно семи.
Ответ: 7.
12. В таблице приведены данные о шести чемоданах.
| Номер чемодана | Длина (см) | Высота (см) | Ширина(см) | Масса (кг) |
| 22,5 | ||||
| 21,5 |
|
|
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 158 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера выбранных чемоданов без пробелов, запятых и других дополнительных символов. Перечисляйте в порядке возрастания номеров.
Решение.
Масса первого чемодана превышает норму багажа.
Сумма трёх измерений для второго чемодана равна 
см, масса удовлетворяет нормам багажа, следовательно, второй чемодан можно сдать в багаж.
Сумма трёх измерений для третьего чемодана равна 
см, что превышает нормы багажа.
Масса четвертого чемодана превышает норму багажа.
Масса пятого чемодана превышает норму багажа.
Сумма трёх измерений для шестого чемодана равна 
см, масса удовлетворяет нормам багажа, следовательно, шестой чемодан можно сдать в багаж.
Ответ: 26.
13. 
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Объем данного многогранника равен сумме объемов параллелепипедов с ребрами 3, 3, 4 и 1, 1, 4:
.
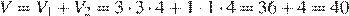Ответ: 40.
14. На рисунке точками показан годовой объём добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали — объём добычи угля в миллионах тонн. Для наглядности точки соединены линиями.
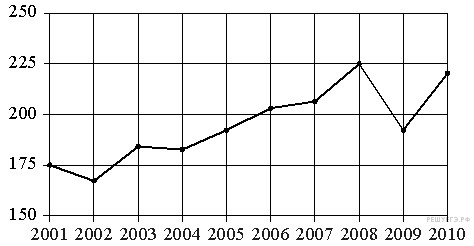
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику добычи угля.
|
|
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ | |
| А) 2001–2003 гг. Б) 2003–2005 гг. В) 2005–2007 гг. Г) 2007–2009 гг. | 1) в течение периода объёмы добычи сначала росли, а затем стали падать 2) объём добычи в этот период рос с каждым годом 3) период с минимальным показателем добычи за 10 лет 4) годовой объём добычи составлял больше 175 млн т, но меньше 200 млн т |
Решение.
А) 2001-2003: из графика видно, что это является периодом с минимальным (меньше 175 млн т) показателем добычи за 10 лет — вариант 3)
Б) 2003-2005: из графика видно, что годовой объём добычи составлял больше 175 млн т, но меньше 200 млн т — вариант 4)
В) 2005-2007: из графика видно, что объём добычи в этот период рос с каждым годом — вариант 2)
Г) 2007-2009: из графика видно, что в течение периода объёмы сначала росли (2007-2008), а затем стали падать (2008-2009) — вариант 1)
Ответ: 3421.
15. 
В окружности с центром O проведён диаметр AB и на окружности взята точка C так, что угол COB равен 120°, AC = 50. Найдите диаметр окружности.
Решение.
Треугольник COA — равносторонний, так как стороны AO = OC как радиусы окружности, а угол COA в нем равен 60° как смежный с углом COB. Тогда диаметр AB = 2 AC = 100.
Ответ: 100.
16. 
В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 6, AC = 18 и AD = 8.
Решение.
Найдём площадь основания пирамиды:
Теперь можем найти объём пирамиды SABC:
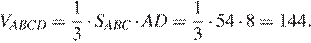
Ответ: 144.
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
| А) 0,5 x ≥ 4 Б) 2 x ≥ 4 В) 0,5 x ≤ 4 Г) 2 x ≤ 4 | 1) 
2) 
3) 
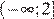4) 
|
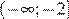
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение.
А) 
(вариант 4).
Б) 
(вариант 2).
В) 
(вариант 1).
Г)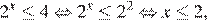 
(вариант 3).
Ответ: 4213.
18. В классе учатся 20 человек, из них 13 человек посещают кружок по истории, а 10 человек — кружок по математике. Выберите утверждения, которые следуют из приведённых данных. В этом классе
1) нет ученика, который не посещает ни кружок по истории, ни кружок по математике
2) найдутся хотя бы два человека, которые посещают оба кружка
3) если ученик не ходит на кружок по истории, то он обязательно ходит на кружок по математике
4) не найдётся 11 человек, которые посещают оба кружка
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение.
1) Утверждение не следует из приведённых данных, поскольку возможна ситуация когда все 13 человек, посещают кружок по истории, причём трое из них посещают ещё и кружок по математике, а оставшиеся семь человек ходят только в кружок по математике.
2) Утверждение следует из приведённых данных. Более того, можно утверждать, что минимум три человека посещают сразу оба кружка. Такая ситуация описана в пункте 1).
3) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда 10 человек из тринадцати, посещающих кружок по истории ходят и на кружок по математике. При этом окажется, что семь человек не посещают ни одного кружка.
4) Кружок по математике посещают 10 человек, поэтому более 10 человек посещать оба кружка не может. Утверждение верно.
Ответ: 24.
19. Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 27. В ответе укажите получившееся число.
Решение.
Если число делится на 27, тогда оно делится на 3 и на 9. Число делится на 9, тогда и только тогда, когда сумма цифр числа делится на 9. Число делится на 3, тогда и только тогда, когда сумма цифр числа делится на 3. Заметим, что, если число делится на 9, то оно делится и на 3 (но необязательно, что делится на 27). Сумма цифр числа 123456 равна 1 + 2 + 3 + 4 + 5 + 6 = 21. Вычеркнув цифры 2, 4 и 6, получим число, сумма цифр которого равна девяти. 135 делится на 27.
Ответ: 135.
20. На палке отмечены поперечные линии красного, желтого и зеленого цвета. Если распилить палку по красным линиям, то получится 6 кусков, если по желтым — 5 кусков, а если по зеленым — 12 кусков. Сколько кусков получится, если распилить палку по линиям всех трех цветов?
Решение.
Распилим на 6 кусков по красным линиям, при распиле по желтым добавится еще 4 куска, а при распиле по зеленым линиям — еще 11 кусков. Всего получится 21 кусок палки.
Ответ: 21.
Вариант № профиль.
1. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
Решение.
С учетом комиссии, Аня должна внести в приемное устройство сумму не менее 300 + 300 · 0,05 = 315 рублей. Значит, минимальная сумма, которую должна положить Аня, — 320 рублей. Проверим, что этой суммы достаточно: 5% от нее составляют 16 руб. (это комиссия), оставшиеся 304 рубля пойдут на счет телефона.
Ответ: 320.
Примечание.
Заметим, что сделанная проверка является важной частью решения. Например, если бы Аня хотела бы положить на счет своего телефона 400 руб., она должна была бы сначала вставить в банкомат 400 + 20 = 420 руб., увидеть, что комиссия составляет 21 руб., а на счет телефона поступит 399 руб., и добавить еще 10 руб. Всего 430 руб.
Приведем другое решение.
После уплаты 5% комиссии на счет телефона остаётся 95% вносимой суммы, которая должна быть не меньше 300 рублей. Если нужно внести x рублей, то 0,95 x ≥ 300, откуда x ≥ 315,7... Поэтому x = 320 руб.
2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января. Ответ дайте в градусах Цельсия. 
Решение.
Из графика видно, что наибольшая температура воздуха 22 января составляла −10 °C (см. рисунок).
Ответ: −10.
3. 
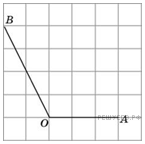Найдите синус угла 
В ответе укажите значение синуса, умноженное на 
Решение.
Проведем высоту 
из точки 
на продолжение стороны 
Тогда:
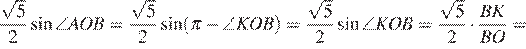
Ответ: 1.
4. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение.
Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52.
Ответ: 0,52.