Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52.
5. Найдите корень уравнения 
Решение.
Последовательно получаем:
Ответ: −4.
6. 
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Решение.
вписанный угол дополняет половину центрального угла, опирающегося на ту же хорду, до 180°. Треугольник AOB является равносторонним, т. к. AO = OB = AB = R, поэтому угол AOB = 60°. Тогда
Ответ: 150.
7. 
На рисунке изображен график функции y = f (x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Решение.
Поскольку касательная параллельна прямой y = 6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y = 6 или совпадает с ней в 4 точках.
Ответ: 4.
8. 
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Решение.
Объемы подобных тел относятся как куб коэффициента подобия, поэтому один из кубов в 2 раза больше другого. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия, поэтому их отношение равно 4.
|
|
Ответ: 4.
9. Найдите значение выражения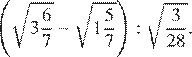 
Решение.
Выполним преобразования:
Ответ: 2.
10. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель − целое число от –2 до 2.
Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид 
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.
Решение.
Обозначим совпадающую оценку по разным показателям 
Поскольку все показатели равны друг другу, все они равны 
Подставим значения в формулу, учитывая, что рейтинг равен 
:
Ответ:10.
11. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
Решение.
Первый обогнал второго на 3 км за четверть часа, это значит, что скорость удаления (сближения) гонщиков равна 
км/ч. Обозначим скорость второго гонщика 
км/ч, тогда скорость первого 
км/ч. Составим и решим уравнение:
|
|
Таким образом, скорость второго гонщика равна 108 км/ч.
Ответ: 108.
12. Найдите точку максимума функции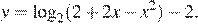 
Решение.
Квадратный трехчлен 
с отрицательным старшим коэффициентом достигает максимума в точке 
, в нашем случае — в точке 1. Поскольку функция 
возрастает, и функция 
определена в точке 1, она также достигает в ней максимума.
Ответ: 1.
13. а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку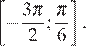 
Решение.
а) Заметим, что: 
Далее имеем:
б) Решая двойное неравенство 
для каждой из полученных серий корней находим, что заданному промежутку принадлежат числа 
и только они.
Ответ: а) 
б) 
14. В правильной треугольной призме ABCA 1 B 1 C 1 известны рёбра: AB 
, AA 1 = 4. Точка M — середина ребра BC.
а) Докажите, что прямые B 1 C и C 1 M перпендикулярны.
б) Найдите угол между прямой C 1 M и плоскостью грани ABB 1 A 1.
Решение.
а) Поскольку
,
получаем
,
то есть прямые 
и 
перпендикулярны.
б) Пусть 
— середина 
, тогда угол между прямой 
и плоскостью грани 
равен углу между этой плоскостью и прямой 
.
Обозначим через 
перпендикуляр, опущенный на 
. Прямая 
перпендикулярна плоскости грани 
, поскольку она перпендикулярна прямым 
и 
. Поэтому искомый угол равен углу 
.
В прямоугольном треугольнике 
:
, 
откуда 
Ответ: б) 30 
.
15. Решите неравенство 
Решение.
Определим область допустимых значений:
Заметим, что на ОДЗ знаки 
и 
совпадают, решим неравенство:
откуда 
|
|
С учётом ОДЗ получаем ответ: 
Ответ: (1; 2].
16. Диагональ AC разбивает трапецию ABCD с основанием AD и BC, из которых AD большее, на два подобных треугольника.
а) Докажите, что ∠ ABC = ∠ ACD.
б) Найдите отрезок, соединяющий середины оснований трапеции, если известно, что BC = 18, AD = 50 и 
Решение.
Прямые AD и BC параллельны, поэтому ∠ ACB = ∠ CAD.
Предположим, что ∠ BAC = ∠ ACD, тогда получаем, что прямые AB и CD параллельны и ABCD — параллелограмм. Значит, предположение неверно и ∠ ABC = ∠ ACD.
б) Треугольники ABC и DCA подобны. Следовательно, 
откуда
Опустим из вершины C перпендикуляр CK на основание AD. Тогда 
Значит, ABCK — прямоугольник.
Следовательно,
Пусть M и N — середины оснований AD и BC соответственно, MH — перпендикуляр к AD. Тогда ABMH — прямоугольник. Получаем, что
В прямоугольном треугольнике MNH имеем:
Ответ: 
17. 15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Решение.
Долг на конец месяца:
Долг с учетом процентов:
Выплаты за первые 12 месяцев:
Их сумма равна:
млн руб.
Ответ: 1 866 000 рублей.
18. При каких значениях параметров а и b система 
имеет бесконечно много решений?
Решение.
На координатной плоскости хОу множество точек 
, удовлетворяющих любому из уравнений системы — прямые. А тогда решением системы будут точки пересечения этих прямых. Поэтому исходная система будет иметь бесконечное множество решений в том и только в том случае, когда эти прямые совпадают. Заметим при этом, что вне зависимости от значений параметров первое уравнение системы задаёт не горизонтальную прямую (коэффициент перед 
не равен нулю), а второе − не вертикальную (коэффициент перед 
не равен нулю), значит, оба уравнения в системе можно привести к виду 
. В общем случае две прямые, заданные уравнениями 
и 
совпадают, если, 
и 
(при 
они имеют одну точку пересечения, при 
и 
точек пересечения у них нет). Следовательно, система будет иметь бесконечно много решений в том случае, когда совместна система
где 
и 
Решая систему, получаем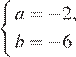 
или 
Ответ: 
, 
19. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 
от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 
от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?
Решение.
а) Если группа состоит из 4 мальчиков, посетивших только театр, 6 мальчиков, посетивших только кино, и 10 девочек, сходивших и в театр, и в кино, то условие задачи выполнено. Значит, в группе из 20 учащихся могло быть 10 мальчиков.
б) Предположим, что мальчиков было 11 или больше. Тогда девочек было 9 или меньше. Театр посетило не более 4 мальчиков, поскольку если бы их было 5 или больше, то доля мальчиков в театре была бы не меньше 
, что больше 
Аналогично, кино посетило не более 6 мальчиков, поскольку 
но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию.
В предыдущем пункте было показано, что в группе из 20 учащихся могло быть 10 мальчиков. Значит, наибольшее количество мальчиков в группе — 10.
в) Предположим, что некоторый мальчик сходил и в театр, и в кино. Если бы вместо него в группе присутствовало два мальчика, один из которых посетил только театр, а другой — только кино, то доля мальчиков и в театре, и в кино осталась бы прежней, а общая доля девочек стала бы меньше. Значит, для оценки наименьшей доли девочек в группе можно считать, что каждый мальчик сходил или только в театр, или только в кино.
Пусть в группе 
мальчиков, посетивших театр, 
мальчиков, посетивших кино, и 
девочек. Оценим долю девочек в этой группе. Будем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится.
Из условия:
значит, 
Тогда 
, поэтому доля девочек в группе:
Если группа состоит из 4 мальчиков, посетивших только театр, 6 мальчиков, посетивших только кино, и 9 девочек, сходивших и в театр, и в кино, то условие задачи выполнено, а доля девочек в группе равна 
Ответ: а) да: б) 10; в) 