Замечания о манипуляциях с геометрией

1) При выполнении таких действий, как вращение кривой или других видах движения, начальная кривая может совпадать с конечной при этом в нижнем окне выдается сообщение о соединенных точках и кривых. Иногда окружности или кривые разбиваются на части при этом исходные кривые сохраняются. В последствии вы можете по ошибке, где-то указать не ту кривую, например проассоциировать блок не с четвертью окружности, а с третью да ещё с вырезом, возможно некорректное создание поверхностей по кривым Во избежание таких несчастий надо очень внимательно следить за геометрией, своевременно создавать соответствующие части, удалять мусор. Если это горе всё-таки произошло заметить его можно, например если на одной кривой лежит две кривые, то при выделении одна из них подсвечивается пунктиром, можно подвести мышь к кривой и выделить её затем щёлкнуть по ней ещё раз, если при этом выделилась некоторая соседняя кривая, то всё в порядке, если же ничего не изменилось (или, например, на окружности загорелся какой-то мусор) или подсветка стала ярче, то лучше удалить этот хлам, проще оставлять его в части GEOM и при провождении ассоциаций или других действий эту часть отключать из видимости.

Удалять следует дубликаты кривых (для этого надо либо вовремя создавать части, либо пользоваться деревом вида, узнавать имена дубликатов, впоследствии копировать их в имена удаляемых кривых).

2) Не стоит лишний раз создавать и удалять геометрию. Если вы отменяете действия, то надо отменять его полностью (иногда отмена одного действия может потребовать нескольких нажатий кнопки назад), в противном случае возможны проблемы из пункта один.

3) Не стоит лишний раз проводить операции соединения или разбиения для поверхностей. Дело в том, что поверхности в ICME хранятся в двух видах: параметрически и численно, операцию слияния можно проводить только для численных, недостатки перевода в это состояние очевидны. При операции разбиения возможна (всё из-за той же толерантности) некорректная перепараметризация (трещины, разрывы, и более жёсткие искажения).

4) При построении поверхностей путём движения кривых (вращение кривой, движение кривой вдоль кривой), каждая движимая кривая создаёт одну поверхность за один этап. Так как операция слияния и разбиения работает корректно для кривых, то желательно заранее знать сколько нужно поверхностей.

Продолжаем построение геометрии. Ещё раз прочитаем замечание №4 и убедимся, что полоска из сглаживающей плоскости нам не нужна, поэтому склеим отрезок LN, с соответствующей дугой, для этого нажмём: , затем выберем соответствующие кривые, нажимаем колесо. Теперь тоже самое делаем для отрезка MO и соответствующей дуги. Заметим, что подобные сглаживания нужны, если строимая сетка будет меньше, чем размер сглаживающих дуг, в противном случае сглаживание бесполезно; что касается физики производства этих “стенок”, то там на самом деле имеет место некоторое оплавление углов при их отливки. Рисунок со скруглениями, здесь не представлен, т.к в подобном масштабе он ничем не отличается от приведённого; поэтому далее будем подразумевать под кривыми LN и MO соответствующие отрезки с приклеенными дугами. Больше ничего не склеиваем, т.к ко всем остальным кривым (включая дуги CD и C1D1), после вращения будут “прикреплены”, соответствующие блоки.

Первый этап построения первого тела закончен, сохраняем эту “фигуру” в часть: щёлкаем правой кнопкой по слову Part в дереве вида, выбираем создать часть, в появившемся окне вводим имя новой части PART.T_1_0, около строчки выбора (), нажимаем на ,зажимаем левую кнопку и обводим все точки и кривые представленные на рисунке (предварительно, не забыв, включить нужные из этих кнопок - в этом случае достаточно выбрать только точки и кривые), нажимаем на колесо.

Приступаем ко второй стадии построения: будем вращать исходную геометрию. Для того чтобы впоследствии не сталкиваться с операциями разбиения поверхностей вращения на четыре плоскости (ровно столько нужно для ассоциации четырёх боковых граней блока), сразу будем вращать геометрию последовательно на углы 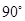. Нажимаем , затем , в этом поле , введём цифру 90, здесь , нажмём на , выберем точки с координатами: Q(0 0 0), Q1(0 0.06 0) (если они не созданы их надо создать), эти точки характеризуют ось вращения, в качестве таких точек можно взять любую пару лежащую на оси Y. Так как вращать будем четыре раза удобно скопировать отобразившиеся имена точек: , в буфер обмена (клавиши Ctrl-Insert), чтобы в последствии не тратить время на выделение, а только вставлять это значение (клавиши Shift-Insert), (вообще все горячие клавиши можно узнать нажав на справку и найдя пункт Hot Keys).

В поле , нажав , вводим кривые, выбирая их все сразу мышью (если все элементы выбираемой геометрии принадлежат одной части, то удобно выбирать сразу всю часть: в появившемся меню выбора надо нажать , а в всплывшем окне поставить галочку напротив нужной части, в данном случае это часть PART.T_1_0, можно выбирать несколько частей). Получим нечто похожее на то что представлено справа. Если поверхности не видно, то либо не стоит соответствующей галочки в дереве видов, либо не выбрана опция Solid для поверхностей.

Замечание: если вы выбирали геометрию из всей части или обводя всю фигуру мышью, среди выбираемых элементов могли оказаться точки, при вращении они не окажут никакого влияния на фигуру вращения, даже если не было выбрано ни одной точки то программа сама создаст их на пересечении прямых образа, а также дуги соответствующие границам поверхностей.

Теперь выделяем, аналогично, образ исходной фигуры, не забыв вставить точки вращения из буфера (использование буфера полезно ещё и тем, что если вы случайно введёте точки вращения не в том порядке, то фигура будет вращаться в другую сторону); повторяем операцию вращения последних образов кривых (цифру 90 не убираем), до тех пор пока фигура не станет иметь вид похожий на тот, что справа. Заметим, что на указанных рисунках уже добавлены “крышки” сверху и снизу. Для удобства работы с геометрией верхняя воронка (плоскости соответствующие вращающимся дугам CD и C1D1) объединены в отдельную часть PART.T_1_1, а так же часть соответствующую невидимым поверхностям образованных вращением кривой МОС1 – часть PART.T_1_2 (по умолчанию оставшийся кусок будет в части PART.T_1_0). Стратегия построения такова, что в дальнейшем планируется описать эту фигуру тремя блоками соответствующими: нижней воронке (образовалась после вращения MO и LN), цилиндру (после вращении NC и OC1), уже оговоренной верхней воронке. Для того чтобы можно было корректно проассоциировать верхние грани блока должны быть созданы плоскости соответствующие внутренностям окружностей образованных после вращения точек O и C1.

Возможен вопрос: для чего разбивать на три блока. Формально всю эту трубку можно описать одним блоком (не включая центрального разбиения: 0-grid), проассоциировав его рёбра с кривыми образующимися путём вращения исходного профиля. Но реально в местах резкого изменения топологии (дуга окружности, сужение), ассоциация будет некорректной (для просмотра качества блока есть соответствующие опции).

Теперь строим эти “крышки” выбираем: , выбираем метод построения, заполняем , незабываем поставить толерантность: , выбираем по четыре кусочка кривых и жмём на колесо. В результате получаем четыре дополнительных плоскости: верхняя и нижняя крышки, и окружности соответствующие вращению точек O и C1; для того чтобы удобнее было строить эти круги, можно либо отключить видимость ненужных частей, либо отключить видимость поверхностей, либо снять опцию solid с поверхностей.

Создание блоков

Только что была создана геометрия первого тела, при её создании использовался подход “снизу-вверх”. Для создания блоков часто используют подход “сверху-вниз”. Для этого выбираем вкладку блоков (), нажимаем , сюда вводим название части в которой будет сохранён блок , (блок обязательно должен быть в какой-то части); теперь вот здесь , нажимаем , выделяем всю геометрию, щёлкаем на колесо. Теперь разобьём на четыре внешних и один внутренний при помощи центрального разбиения (0-grid Block), такое разбиение нужно, чтобы описать как стенку блока (с учётом её толщины), так и его внутренность. Нажимаем , выбираем , вот здесь , нажимаем и выбираем блок. Далее надо указать как будет располагаться внутренний блок (верхние грани лежат в одной плоскости, верхняя и нижняя, боковая, и т.д.); нажимаем здесь на и выбираем верхнюю и нижнюю грань, т.е. эти грани будут лежать в одной плоскости. Вот здесь , ставим отношение , где 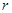- радиус внутреннего блока, 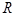- радиус внешнего (эта опция служит более для удобства изображения, т.к. после ассоциации все вершины блока итак будут передвинуты к соответствующим точкам, т.е. можно оставлять значение по умолчанию – 1). Если поставить галочку здесь , то “кольцевой” блок будет строится вокруг исходного.

Если что-то сделано неправильно, то надо нажать и повторить всё заново. Сейчас всё готово для создания блока, нажимаем . Теперь выбираем , ставим вот здесь флажок , и выделяем все блоки, щёлкаем колёсиком, теперь выбираем , как всегда здесь нажимаем и выбираем на экране произвольное вертикальное ребро и разбиваем его в “районе” точек С и С1 (если вы попали по ребру неудачно секущую плоскость можно двигать до тех пор пока не нажато колесо). Пользуясь этим же методом разбиваем нижнюю группу блоков в “окрестности” точек N и О. Создаём части: верхнюю группу блоков называем B_1, среднюю – В_2, нижнюю – В_3. Полученное нарисовано справа.

Настало время проводить ассоциации. Нажимаем , затем , поочерёдно нажимая на вершину, затем на соответствующую точку проводим ассоциацию (колёсико нажимать необязательно), при этом геометрическое место вершин блока переносится в те точки с которыми их ассоциируют. После этого ассоциируем рёбра блока с кривыми. Нажимаем , затем так же попарно выделяем сначала ребро, затем кривую. Проассоциированные рёбра начинают подсвечиваться зелёным цветом (о дополнительных настройках смотреть выше).

Ассоциируем поверхности, для этого удобно отключить из видимости, сначала, все ненужные части, теперь нажимаем , в пункте метод ставим здесь галочку: , затем выделяем все грани блока В_2 (обводим его мышью его внешние грани, чтобы достоверно видеть что выбрались нужные грани удобно опцию Solid с блока на некоторое время снимать), щёлкаем колёсиком, в появившемся окне ставим галочку напротив части PART.T_1_0 (внешность трубки; выделяем внутренние грани блока и аналогично ставим галочку около части PART.T_1_2; также ассоциируем верхние и нижние крышки блока; так же ассоциируются четыре верхних и четыре нижних “четвертинки” колец с поверхностями образованными при вращении отрезков ON и СС1 (заметьте, что при таком удачном “предвидении” будущих ассоциаций не надо проводить никаких лишних действий). Аналогично поступаем со всеми остальными блоками. Только не забудьте сразу отправить в отдельные части вход и выход из тела (верхний и нижний круги), т.к. если об этом спохватиться позже придётся у соответствующих граней менять ассоциации. Результат приведён справа.

Построение сетки

Для этого нажимаем , затем сюда , при этом слева появляется нижеприведённое меню.

Это поле позволяет выбрать разбиваемое ребро, после того как имя разбиваемого ребра при помощи мыши и колёсика скопировано в это поле (иногда это тоже получается со второй попытки), можно приступать к заполнению остальных пунктов. В поле высвечивается длина выбранного ребра. В пункте , указывается число узлов на этой грани. Закон разбиения ребра указывается в этом поле . Существует целый ряд законов разбиения: 1) BiGeomertic – позволяет проводить равномерное разбиение рёбер. 2) Exponential1 – можно экспоненциально сгущаться к концу ребра, чтобы полностью задать экспоненциальное разбиении надо ещё заполнить поля и , они характеризуют значения, соответственно, первого (в начале ребра) и последнего (в конце) элемента, естественно, что при фиксированном законе разбиения и числе узлов это выполнить “трудно”, поэтому справа на сером фоне подсвечиваются более точные значения (внимательно смотрите за ними, т.к. ваши “желания” не всегда будут выполняться корректно); при использовании разбиения Exponential1 важно, чтобы второе значение было больше первого.

Если надо сгустится не к концу ребра, а к началу, надо выбрать разбиение Exponential2 и задавать уже второе значение меньше первого. 3) FullCosinus – одно из самых гибких видов разбиения, оно позволяет задавать значения элементов как вначале, так и в конце ребра (выполняется всегда, если их размер не превосходит максимального, в противном случае их размер приравнивается к максимальному), при помощи поля , можно задавать ограничения на максимальный элемент, если в это поле заполнено значение 0, то ограничений нет; после того как эти поля заполнены, производится сглаживание сетки от каждого из краёв к центру ребра, т.е. в центре ребра всегда оказывается наибольший или наименьший элемент; таким образом, при помощи данного закона очень удобно делать близкие к симметричным разбиения со сгущением к краям или к центру ребра (естественно надо заполнить поле с количеством узлов). 4) Geometric1 позволяет сгущаться по линейному закону к концу ребра, Geometric2 – линейно сгущаться к началу (замечания касающиеся первых и последних шагов разбиения переносятся из пункта об экспоненциальных разбиениях). 5) Все вышеперечисленные законы хороши, но самыми общими являются следующие: Spline и Linear. Несмотря на то что они выделены в два отдельных закона при их выборе открывается одно и тоже меню, которое приведено снизу. Изучить это меню достаточно полезно. Главной особенностью этого меню является то, что все приведённые здесь функции можно редактировать, для этого просто надо “захватить” левой кнопкой мыши любую из красных точек и установить её в нужное положение, щелчком левой кнопки мыши по любой точке меню можно создать новые опорные (красные) точки и их так же можно двигать (чтобы убрать красную точку дважды щёлкните по ней левой кнопкой), не выходя из этого меню можно менять кусочно-линейный закон (Linear), на закон Spline и обратно. Нажмите кнопку - чтобы уйти из режима интерполяции сплайнами в линейный режим, чтобы перейти из линейного режима (точки просто соединены отрезками) в режим сплайнов надо нажать кнопку , которая будет гореть на том же месте где до этого горела кнопка . Удобной частью интерфейса является то, что размеры элементов пронормированы таким образом, что минимальному элементу соответствует максимальное значение на вертикальной шкале (самое большее всегда равно 1, поэтому удобно точку с минимальным значением сразу ставить на единичную высоту), поднимая и опуская график (с помощью движения точек), можно видеть во сколько раз разбиение в этом месте крупнее минимального, аналогично отношение высот любых двух точек графика (красные точки необязательно лежат на графике, например при разбиении сплайном), даёт отношение длин соответствующих отрезков разбиения. Если поставить соответствующую галочку, то можно заполнять поля Set First и Set Last, но будьте внимательны эти значения никак не повлияют на закон разбиения, т.е. сначала будет выполнено разбиение, а потом только длины первого и последнего элемента будут заменены введёнными значениями (поэтому сначала лучше разбивать ребро так, чтобы первый и последний элемент были примерно нужной длины, а потом только ставить более точные размеры).

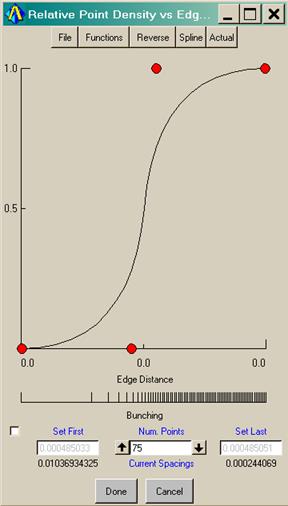
На отрезке снизу: , представлен качественный характер будущего разбиения, он является только качественным, т.к. число узлов разбиения на нём задаётся в поле представленном на рисунке справа.

Чтобы выполнить это разбиение ещё и количественно (т.е. чтобы минимальный, максимальный, первый и последний элемент остались такими же), надо не забыть после выхода из этого меню проставить нужное число узлов в меню представленном на страницу выше. Если надо сгущаться не к началу ребра, а к концу, то надо нажать на кнопку и нажать , если надо отразить график сверху вниз, то нажать .

Если горит кнопка , то значения первого и последнего элемента выдаются в истинных размерах, если на неё нажать, то на её месте загорится кнопка , тогда ось Ох также пронормируется на единицу и на соответствующих местах будет показываться отношение длины элемента к длине всего ребра. Одним из применяемых в этой работе было разбиение Parabola Ends, которое можно увидеть во вкладке функций (кнопка ), при этом его центральная часть была несколько поднята (т.е. уменьшены наибольшие элементы); профиль этого разбиения можно увидеть справа.

В некотором смысле это аналог разбиения по полному косинусу (FullCosinus), только более удобный в управлении. После того как разбиение сконструировано, нажимаем на кнопку .