При входном воздействии eat изображение функции будет иметь вид:

Для нахождения нужного тока вычисляем определитель:
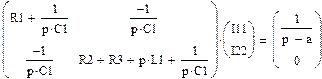
Найдем Δ(p):

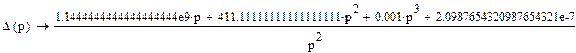
Найдем Δ2(p):
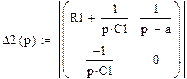
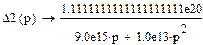
Найдем ток I22:

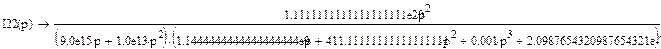
Найдем выходное напряжение Uвых(p):
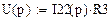
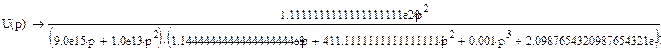
Выходной сигнал представляет собой дробь N(p)/M(p), где:
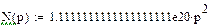
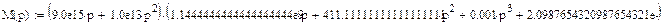
Найдем корни уравнения M(p):

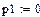
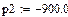
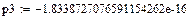
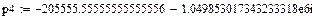
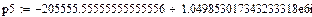
Найдем производную М'(р):

Найдем М1'(р), М2'(р), М3'(р), М4'(р), М5'(р) и М6'(р):

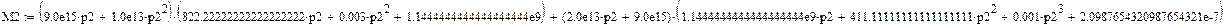
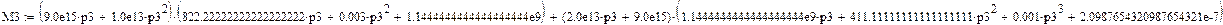

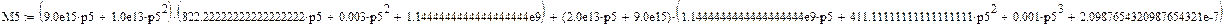
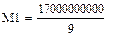
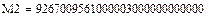
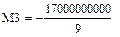

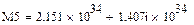
Найдем N1(р) и N2(р):

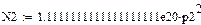
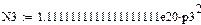
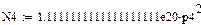
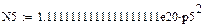


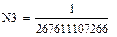
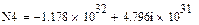

Используя формулу разложения, найдем оригинал выходного сигнала:
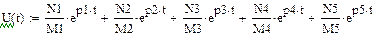
Получим выходной сигнал:
График временной зависимости при заданном входном сигнале eat:
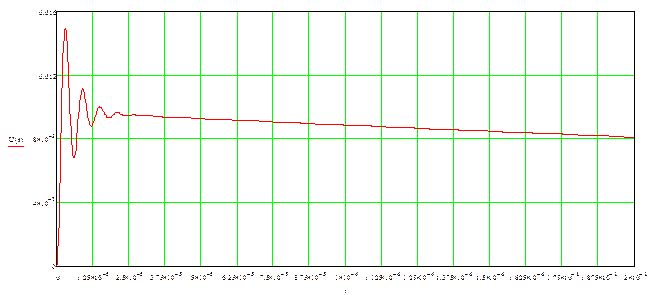
Рисунок 7 – Временная зависимость выходного сигнала при заданном входном сигнале в Mathcad

Рисунок 8 – Временная зависимость выходного сигнала при заданном входном сигнале в microcap

Рисунок 9 – Временная зависимость выходного сигнала при заданном входном сигнале в Mathcad
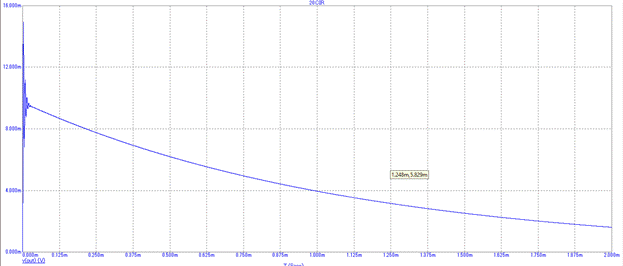
Рисунок 10 – Временная зависимость выходного сигнала при заданном входном сигнале в microcap
Заключение
В ходе выполнения расчетного задания был изучен операторный метод расчета переходных процессов, была построена система линейных уравнений в матричном виде, найдены напряжение и изображение выходного сигнала, а также конечной выходной характеристики и построены графики переходной и импульсной характеристик, а также график временной зависимости выходного сигнала при заданном входном сигнале.
В результате исследования переходной характеристики были получены 2 комплексно-сопряженных корня и один мнимый. Третий корень появился из-за особенности расположения конденсатора, он подключен параллельно, следовательно, постоянная составляющая имеет место быть в электрической цепи.
|
|
В результате исследования импульсной характеристики также были получены два комплексно-сопряженных корня и один мнимый.
При расчете временной зависимости выходного сигнала при заданном входном сигнале получились один нулевой корень, два мнимых и пара комплексно-сопряженных. Это обусловлено особенностью входного воздействия заданной функцией.
Добротности контура достаточно для наблюдения затухающих колебаний, та как во всех трех случая имеются комплексно-сопряженные корни.
Список используемых источников
1 Е. М. Патрушев. Преобразование измерительных сигналов. Электронный учебно-методический комплекс. [Текст] / Е. М. Патрушев., Патрушева Т.В. – АлтГТУ им. И.И.Ползунова, – Барнаул, 2009. – 224 с.
2 Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп [Текст] / Бессонов Л.А. –М.: Высш. шк., 1978. –528с.
3 К.М. Поливанов. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М. Поливанова. Т.1. К.М. Поливанов. Линейные электрические цепи с сосредоточенными постоянными [Текст] – М.: Энергия- 1972. –240с.
4 Г.В. Зевеке. Основы теории цепей: Учеб. для вузов [Текст] Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. – 528с.
5 Расчет переходных процессов [Электронный ресурс]: – Режим доступа: https://ets.ifmo.ru/osipov/os1/3_5_0.htm. – Загл. с экрана.
6 Преобразование Лапласа [Электронный ресурс]: – Режим доступа: https://mathhelpplanet.com/static.php?p=preobrazovaniye-laplasa-i-yego-svoystva. – Загл. с экрана.
|
|