Непосредственный подсчет вероятности

Лекция 3

Классическая формула вычисления вероятности.

 

Предположим, что в эксперименте имеется полная группа элементарных событий.

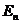, …, . Тогда каждое событие из W имеет вид

, (2.1)

где - некоторое подмножество множества .

Следовательно, по свойству 4 вероятности

Таким образом, в случае конечного эксперимента вероятность лю­бого события определяется вероятностями элементарных событий (исходов).

Для многих конечных экспериментов из соображений симметрия можно априори установить, что элементарные события имеют оди­наковую вероятность. Тогда вероятность каждого элементарного со­бытия равна 1/n (n — число исходов), событие A состоялось в m испытаниях, следовательно, вероятность события A вида (2.1) равна

P (A) = 1/n+1/n+…+1/n = m/n.

Если элементарные события имеют одинаковую вероятность, то они называются равновозможными исходами, а те из них, которые влекут A, - благоприятствующими исходами. Следовательно, в этом случае P (A) равно отношению числа благопри­ятствующих исходов m к числу всех равновозможных исходов n:

(2,1)

Это классическая формула вероятности.

При решении задач на классическое определение вероятности потребуется вычислять число всех равновозможных исходов в экспери­менте, а затем — число благоприятствующих исходов. Обычно это можно сделать комбинаторными методами.

3.2. Основные формулы комбинаторики

 

Комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов любой природы, заданного конечного множества.

Перестановками называются комбинации, состоящие из одних и тех же элементов n различных элементов и отличающиеся друг от друга только порядком их расположения.

Число всех возможных перестановок из n различных элементов равно

где . 0!=1

Пример.

Перестановками с повторениями. Если рассматривать упорядоченные k- последовательности из множества М, которые состоят не только из различных элементов множества М, то получаем перестановки с повторениями

Число 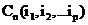различных перестановок с повторениями из множества М равно

Пример. Дано множество . Число перестановок с повторениями

Размещения. Любая упорядоченнаяпоследовательность k различных из множества М составленная из n элементов называется размещением из n элементов по k.

Число различных размещений есть

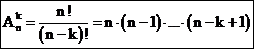
Пример. Число комбинаций призеров в соревновании по волейболу среди команд 5 факультетов

Размещения с повторениями. Любая упорядоченная последовательность k элементов множества М, содержащего n элементов, называетсяразмещениями с повторениями из n по k.

Число размещениями с повторениями есть

.

Пример. Сколькоразличных трехбуквенных слов можно составить из 32 букв алфавита, не обращая внимания на то, имеют ли смысл составленные из букв слова?

Решение. Число различных трехбуквенных слов из 32 букв алфавита составляет =32 768

Сочетаниями называют комбинации 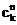, составленные из n различных элементов по k элементов, которые отли­чаются хотя бы одним элементом.

Число сочетаний из n различных элементов по k элементов равно

Пример. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. Искомое число способов =45.

Сочетания с повторениями. Если объединить все размещения с повторениями из n элементов порядка k, состоящие из одинакового из одинакового количества одних и тех же элементов (без учета расположения), в класс эквивалентности, то каждый такой класс называется сочетаниями с повторениями из n элементов по k.

Число различныхсочетаниями с повторениями из n элементов по k

.

.

Пример. При наличии двух неразличимых игральных костей можно получить различных друг от друга комбинаций

Решение. Здесь n=6, k=2, тогда

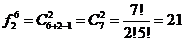
Пример. При бросании трех монет можно получить различных друг от друга комбинаций

Решение. Здесь n=2, k=3, тогда

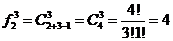
При решении задач комбинаторики используют сле­дующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности

объектов m способами, а другой объект В может быть выбран n способами, то выбрать

либо А, либо В можно m+n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами

Пример. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение.

Обозначим через A событие — набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможные и образуют полную группу. Благоприятствует собы­тию A лишь один исход (нужная цифра лишь одна). Искомая веро­ятность равна отношению числа исходов, благоприятствующих со­бытию, к числу всех элементарных исходов P (A) =1/10.

Пример Экзаменационная программа имеет 40 вопросов. На экзамене надо ответить на 3 из них. Вы подготовили 15 вопросов. Какова вероятность сдачи Вами экзамена?

Решение

Событие А – студент сдал экзамен, то есть ответил на 3 вопроса.

Элементарные события выбора билета несовместны, равновероятны и образуют полную группу. Тогда по классической формуле вероятности

Ответ. =0.04605

3.3. Геометрические вероятности.

 

Это вероятности в экспе­риментах с бесконечным числом исходов, которые интерпретируются как выбор наудачу точки из некоторого множества в размером 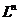. Предпо­лагается, что множество имеет некоторую геометрическую форму. Событием А назовем следующее: выбранная точка принадлежит задан­ной части фигуры размером . Вероятность такого события Р(А) определим как отно­шение объема (площади, длины) части фигуры к объему 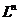(площади, длине) всей фигуры

.

Пример. Две точки независимо друг от друга наудачу выбира­ются на отрезке [0,1]. Найти вероятность того, что произведение координат точек будет больше 0.4.

Решение.

При бесконечном числе равновозможных элементар­ных исходов, представленных точками области на плоскости, вероят­ность события равна отношению площади множества элементарных исходов, благоприятствующих этому событию, к площади всего мно­жества элементарных исходов.

1. Определяем пространство элементарных исходов.

Пусть x и y — координаты первой и второй точек, выбранных на [0,1]. Тогда каждый элементарный исход представляется упорядоченной парой (x,y) вещественных чисел. Каждой такой паре со­ответствует точка квадрата D = {(х,у): х [0,1], у [0,1]} на плоскости XOY. Наоборот, каждой точке (х,у)квадрата D соот­ветствуют две точки на отрезки [0,1], имеющие координаты х и у, т.е. некоторый исход случайного эксперимента.

Итак, пространство элементарных исходов совпадает с квадра­том D. Выбрать две точки отрезка [0,1] — это то же самое, что выбирать одну точку квадрата D.

2. Проверяем равную возможность элементарных исходов.

В данном случае она гарантирована методикой проведения слу­чайного эксперимента, поскольку, как сказано в условии задачи, обе точки выбираются на отрезке наудачу. Соответственно, ни один из участков квадрата D не является более предпочтительным, чем лю­бой другой равный ему по площади участок квадрата D.

3. Отбираем те элементарные исходы, которые приводят к на­ступлению интересующего нас события (благоприятные исходы).

Нас интересует вероятность события А = {xy> 0.4}. Ему соот­ветствует область G = {(х,у): ху > 0.4} D (см. рис. 6.1).

 

4. Находим площадь S(D) области D. Очевидно, что S(D) = 1.

5. Находим площадь S(G) области G. Имеем

6.

7. Согласно геометрическому определению вероятности

Ответ. Р(А) = =0.2335

Пример (задача о встрече). Два лица договариваются о встрече на заданном промежутке времени T. Лицо, пришедшее пер­вым, ожидает в течение времени t < T, затем уходит. Какова ве­роятность встречи?

Решение. В качестве множества элементарных событий рассмотрим квад­рат, состоящий из точек (x, у), 0 x T, 0 у T, где x и у — время прихода первого и второго лица.

Благоприятствующие исходы образуют точки, для которых , то есть точки квадрата между прямыми y = x – t, y = x + t.

Площадь этой фигуры P = (.

 

Пример. Геометрические вероятности (неограниченная область)

Плоскость разбита прямыми на квадратные клетки со стороной а. Клетки пронумерованы при помощи пар целых чисел (m, n)(при этом у соседней справа клетки будет номер (m+l,n), а у соседней сверху клетки будет номер (m,n+1)). Найти вероятность того, что брошенная наудачу на плоскость монета радиуса r < а/2— целиком попадет в какую-нибудь клетку, для которой m + nкратно трем.

Решение. Бросание монеты наудачу равносильно выбору на­удачу точки, в которой будет расположен центр монеты. Искомая вероятность равна отношению площади области благоприятных ис­ходов в одной ячейке к площади всей ячейки.

1. Определяем пространство элементарных исходов

В данном случае им является любая из равных прямоугольных ячеек, на которые разбивается плоскость и которые содержат рав­ные части множества благоприятных исходов G и равные части его дополнения до всей плоскости. Обозначим такую ячейку символом D. Чтобы найти D, заметим, что если некоторая клетка (m, n) удовле­творяет требуемому условию, то ему удовлетворяют и клетки (m + 3, n), (m - 3, n), (m, n + 3), (m, n -3), т.е. имеет место перио­дичность по горизонтали с периодом 3 и по вертикали с периодом 3. Поэтому в качестве ячейки D можно взять область, составленную из клеток (0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1) и (2,2).

2. Проверяем равновозможность элементарных исходов.

В данном случае она гарантирована методикой проведения слу­чайного эксперимента, поскольку, как сказано в условии задачи, мо­нета бросается наудачу.

 

 

3. Отбираем те элементарные исходы, которые приводят к на­ступлению нтересующего нас события (благоприятные исходы).

Ясно, что среди клеток ячейки D сумма

Рис. 6.2

координат m+n делится на три только у клеток (0,0), (1,2) и (2,1).

Для того чтобы монета оказалась внутри некоторой клетки, не­обходимо и достаточно, чтобы центр монеты находился в одной из точек, расположенных внутри клетки на расстоянии большем r от границы этой клетки. На рис. 6.2 изображена ячейка D и заштрихо­вана область благоприятных исходов G DD.

4. Находим площадь S(D)ячейки D. Имеем S(D) = 9а².

5. Находим площадь S ()области . Имеем S () = 3(а – 2r)².

6. Искомая вероятность равна

 

Ответ. (а-2г)²/(3а²).