Обяснение нового материала.

Тема:Механическая работа. Мощность

Цель урока: расширить знания о механической работе и мощности. Дать представления об особенностях работы силы тяжести, упругости, трения.

Задачи.

Образовательные: обобщить и систематизировать знания о механической работе и мощности, полученные в седьмом классе. Дать понятие о работе силы тяжести, упругости и трения.

Развивающие: научить видеть вокруг физические явления и уметь их правильно объяснять; умения анализировать, сравнивать и делать выводы; развитие мыслительной деятельности учащихся.

Воспитательные: воспитывать внимательность, познавательный интерес к предмету; расширять кругозор, формировать умение строить логическую цепочку рассуждений.

Оборудование: динамометр, брусок.

Ход урока

1. Организационный момент

На данном уроке мы рассмотрим две физические величины: механическую работу и мощность. Узнаем, от чего зависит тот факт, что работа бывает положительной, отрицательной и равной нулю, а также покажем, как связаны между собой работа и мощность. В конце урока мы разберём, как, зная мощность, можно найти скорость транспортного средства.

2.Актуализация знаний.

На про­шлых уро­ках мы узна­ли о фи­зи­че­ских ве­ли­чи­нах, ко­то­рые на­зы­ва­ют­ся «им­пульс тела» и «импульс силы»

1.Ответить на вопросы:

v Что называется импульсом?

v - Почему импульс – векторная величина?

v - Назовите единицы измерения импульса тела в СИ.

v - В чем заключается закон сохранения импульса?

v - Напишите формулу закона сохранения импульса в векторном виде.

v - При каких условиях выполняется этот закон?

v - Какую систему называют замкнутой?

v - Кем и когда был впервые сформулирован закон сохранения импульса?

v - Почему происходит отдача при выстреле из ружья?

v Рассмотрим упругое и неупругое взаимодействие:

v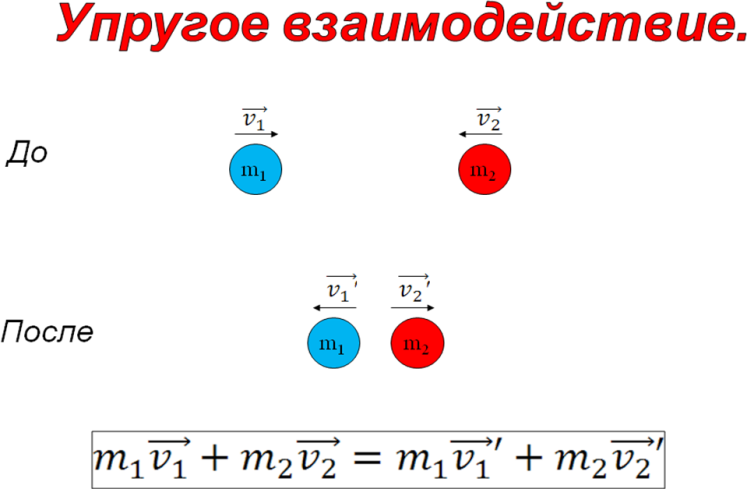

 

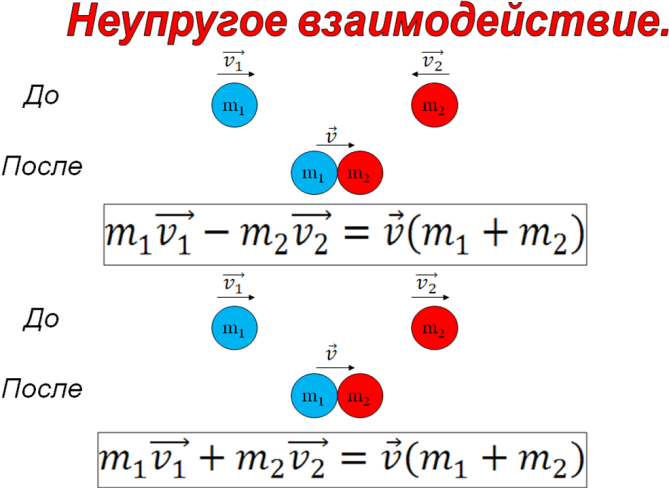
2.Решить задачу:

Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия, если удар неупругий?

 

Обяснение нового материала.

Как нам из­вест­но, из­ме­не­ние им­пуль­са тела свя­за­но с дру­гой фи­зи­че­ской ве­ли­чи­ной, ко­то­рая на­зы­ва­ет­ся им­пуль­сом силы. На этом уроке, тема ко­то­ро­го «Ме­ха­ни­че­ская ра­бо­та. Мощ­ность», ана­ло­гич­ным об­ра­зом по­ка­жем, что из­ме­не­ние энер­гии тела также свя­за­но с дру­гой фи­зи­че­ской ве­ли­чи­ной – ра­бо­той силы. Механическая работа

В курсе фи­зи­ки 7-го клас­са мы узна­ли, что если тело под дей­стви­ем неко­то­рой силы 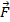со­вер­ша­ет пе­ре­ме­ще­ние 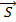(см. Рис. 1) в на­прав­ле­нии дей­ствия силы, то сила со­вер­ша­ет ра­бо­ту A, рав­ную про­из­ве­де­нию мо­ду­ля силы на мо­дуль пе­ре­ме­ще­ния.

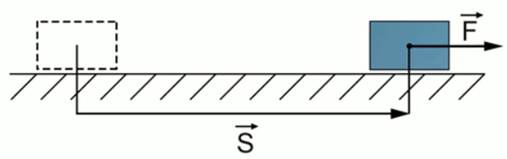
Рис. 1. Пе­ре­ме­ще­ние тела под дей­стви­ем силы F

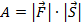
Еди­ни­цей из­ме­ре­ния ра­бо­ты в си­сте­ме СИ яв­ля­ет­ся джо­уль – ра­бо­та силы в 1 Н при пе­ре­ме­ще­нии точки ее при­ло­же­ния на 1 м:

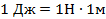
Дан­ное опре­де­ле­ние ра­бо­ты огра­ни­че­но толь­ко слу­ча­ем, когда на тело дей­ству­ет един­ствен­ная сила, ко­то­рая с пе­ре­ме­ще­ни­ем яв­ля­ют­ся со­на­прав­лен­ны­ми век­то­ра­ми. По­это­му необ­хо­ди­мо обоб­щить дан­ную фор­му­лу ра­бо­ты для си­ту­а­ции, когда пе­ре­ме­ще­ние про­ис­хо­дит в на­прав­ле­нии, не сов­па­да­ю­щем с на­прав­ле­ни­ем дей­ствия силы, и когда на тело дей­ству­ет несколь­ко сил.

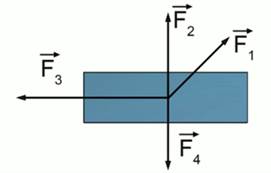
Рис. 2. На тело дей­ству­ет несколь­ко сил

Если на тело дей­ству­ет несколь­ко сил (см. Рис. 2), то в этом слу­чае необ­хо­ди­мо в фор­му­лу для ра­бо­ты под­став­лять зна­че­ние рав­но­дей­ству­ю­щей всех сил. Сле­до­ва­тель­но, ра­бо­та будет равна сумме всех работ от­дель­ных сил.

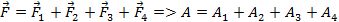
Рав­но­дей­ству­ю­щая может быть равна нулю, даже если от­дель­ные силы не ну­ле­вые. В этом слу­чае ра­бо­та также долж­на быть рав­ной нулю, по­это­му, в со­от­вет­ствии с фор­му­лой 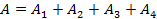, ра­бо­ты от­дель­ных сил долж­ны быть с раз­ны­ми зна­ка­ми (могут быть от­ри­ца­тель­ны­ми или по­ло­жи­тель­ны­ми). Таким об­ра­зом, необ­хо­ди­мо фор­му­лу для вы­чис­ле­ния ра­бо­ты при­ве­сти к та­ко­му виду, чтобы можно было по­лу­чать как по­ло­жи­тель­ные, так и от­ри­ца­тель­ные зна­че­ния этой ве­ли­чи­ны. Из курса гео­мет­рии из­вест­но, что опе­ра­ция, поз­во­ля­ю­щая при умно­же­нии век­то­ров по­лу­чать число (по­ло­жи­тель­ное или от­ри­ца­тель­ное), на­зы­ва­ет­ся ска­ляр­ным про­из­ве­де­ни­ем век­то­ров.

Ме­ха­ни­че­ской ра­бо­той на­зы­ва­ет­ся ве­ли­чи­на, рав­ная ска­ляр­но­му про­из­ве­де­нию рав­но­дей­ству­ю­щей сил, дей­ству­ю­щих на тело, на пе­ре­ме­ще­ние тела.

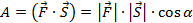
Если угол между век­то­ра­ми рав­но­дей­ству­ю­щей силы и пе­ре­ме­ще­ния ост­рый, то ра­бо­та по­ло­жи­тель­ная (см. Рис. 3).

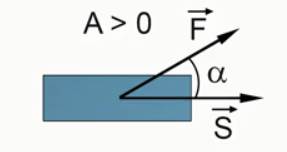
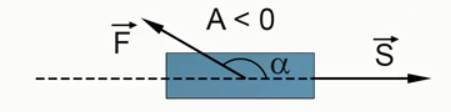
Рис. 3. Ост­рый угол между век­то­ра­ми рав­но­дей­ству­ю­щей силы и пе­ре­ме­ще­ния Рис. 4. Тупой угол между век­то­ра­ми рав­но­дей­ству­ю­щей силы и пе­ре­ме­ще­ния

Если угол между век­то­ра­ми рав­но­дей­ству­ю­щей силы и пе­ре­ме­ще­ния тупой, то ра­бо­та от­ри­ца­тель­на (см. Рис. 4).Для при­ме­ра: когда че­ло­век с по­мо­щью ве­рёв­ки тащит за собой санки, ве­рёв­ка об­ра­зу­ет с на­прав­ле­ни­ем дви­же­ния санок ост­рый угол (см. Рис. 5). Сле­до­ва­тель­но, ра­бо­та силы, с ко­то­рой че­ло­век тянет санки, имеет по­ло­жи­тель­ный знак.

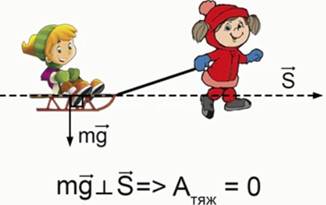
Рис. 5. Ра­бо­та силы, с ко­то­рой че­ло­век тянет санки Рис. 6. Сила тя­же­сти не со­вер­ша­ет ра­бо­ту

На­прав­ле­ние рав­но­дей­ству­ю­щей силы может быть пер­пен­ди­ку­ляр­но на­прав­ле­нию пе­ре­ме­ще­ния тела. В этом слу­чае угол между век­то­ра­ми силы и пе­ре­ме­ще­ния равен 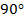. Так как ко­си­нус этого угла равен нулю, то ра­бо­та, со­вер­ша­е­мая дан­ной рав­но­дей­ству­ю­щей силой над телом, равна нулю.Воз­вра­ща­ясь к при­ме­ру с сан­ка­ми, можно ска­зать, что сила тя­же­сти, ко­то­рая дей­ству­ет на санки, пер­пен­ди­ку­ляр­на на­прав­ле­нию дви­же­ния и не со­вер­ша­ет ра­бо­ту (см. Рис. 6).

 

Также не со­вер­ша­ет ра­бо­ту при рав­но­мер­ном дви­же­нии по окруж­но­сти та сила, ко­то­рая вы­нуж­да­ет тело дви­гать­ся таким об­ра­зом, так как эта сила в любой точке окруж­но­сти пер­пен­ди­ку­ляр­на на­прав­ле­нию ско­ро­сти тела. На­при­мер, не со­вер­ша­ет ра­бо­ту сила все­мир­но­го тя­го­те­ния, под дей­стви­ем ко­то­рой ис­кус­ствен­ные спут­ни­ки Земли дви­жут­ся по кру­го­вой ор­би­те.

Мощность

Чаще всего при­клад­ное зна­че­ние ме­ха­ни­че­ской ра­бо­ты по­лез­но при рас­смот­ре­нии ра­бо­ты раз­лич­ных ме­ха­низ­мов.

Пред­по­ло­жим, что нам необ­хо­ди­мо под­нять на крышу зда­ния неко­то­рый груз. В пер­вом слу­чае для этого ис­поль­зу­ем руч­ную ле­бёд­ку, во вто­ром слу­чае – подъ­ём­ный кран.

Время, ко­то­рое за­тра­чи­ва­ет­ся на вы­пол­не­ние ра­бо­ты, во вто­ром слу­чае мень­ше, чем в пер­вом. Сле­до­ва­тель­но, одну и ту же по ве­ли­чине ра­бо­ту можно со­вер­шить за раз­ное время. То есть важно знать, как быст­ро со­вер­ша­ет­ся ра­бо­та. По­это­му вся­кая ма­ши­на, со­вер­ша­ю­щая ра­бо­ту, ха­рак­те­ри­зу­ет­ся осо­бой ве­ли­чи­ной, на­зы­ва­е­мой мощ­но­стью.
Мощ­ность (P) ма­ши­ны или ме­ха­низ­ма равна от­но­ше­нию со­вер­шен­ной ра­бо­ты ко вре­ме­ни, в те­че­ние ко­то­ро­го она со­вер­ше­на.

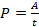
Еди­ни­цей из­ме­ре­ния мощ­но­сти в си­сте­ме СИ яв­ля­ет­ся ватт (Вт):

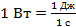
Дан­ная ве­ли­чи­на может быть по­лез­на при рас­чё­те ра­бо­ты, так как для боль­шин­ства устройств, со­вер­ша­ю­щих ме­ха­ни­че­скую ра­бо­ту, мощ­ность из­вест­на за­ра­нее. То есть для под­счё­та ра­бо­ты необ­хо­ди­мо знать мощ­ность и тот про­ме­жу­ток вре­ме­ни, в те­че­ние ко­то­ро­го вы­пол­ня­лась ра­бо­та.

Также мощ­ность ис­поль­зу­ет­ся для рас­чё­та ско­ро­сти раз­лич­ных транс­порт­ных средств. Са­мо­лё­ты, ко­раб­ли, ав­то­мо­би­ли и т. д. часто дви­жут­ся таким об­ра­зом, что их ско­рость, с хо­ро­шей точ­но­стью, можно счи­тать по­сто­ян­ной ве­ли­чи­ной. Если дви­же­ние про­ис­хо­дит с по­сто­ян­ной ско­ро­стью, то силы, дей­ству­ю­щие на транс­порт­ное сред­ство бла­го­да­ря ра­бо­те дви­га­те­ля, равны по мо­ду­лю и про­ти­во­по­лож­ны по на­прав­ле­нию силам со­про­тив­ле­ния дви­же­ния. Ве­ли­чи­на ско­ро­сти транс­порт­но­го сред­ства опре­де­ля­ет­ся мощ­но­стью дви­га­те­ля.

Рас­смот­рим слу­чай, при ко­то­ром сила со­на­прав­ле­на пе­ре­ме­ще­нию (см. Рис. 7).

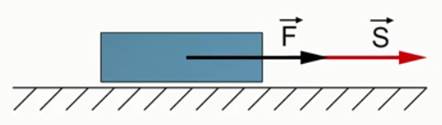
Рис. 7. Дви­же­ние тела под дей­стви­ем силы F

При этом фор­му­ла для вы­чис­ле­ния ра­бо­ты будет вы­гля­деть сле­ду­ю­щим об­ра­зом:

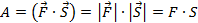Сле­до­ва­тель­но, мощ­ность будет равна:

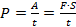От­но­ше­ние мо­ду­ля пе­ре­ме­ще­ния ко вре­ме­ни дви­же­ния тела – это ско­рость тела:

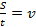
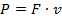
Эта фор­му­ла по­ка­зы­ва­ет, что при по­сто­ян­ной силе со­про­тив­ле­ния ско­рость транс­порт­но­го сред­ства тем выше, чем боль­ше мощ­ность дви­га­те­ля. По­это­му быст­ро­ход­ные транс­порт­ные сред­ства нуж­да­ют­ся в мощ­ных дви­га­те­лях. Также можно сде­лать вывод, что при по­сто­ян­ной мощ­но­сти дви­га­те­ля сила тем выше, чем мень­ше ско­рость дви­га­те­ля.

Итоги урока

На дан­ном уроке мы ввели в рас­смот­ре­ния две фи­зи­че­ских ве­ли­чи­ны: ме­ха­ни­че­скую ра­бо­ту и мощ­ность. Мы по­ка­за­ли, что в за­ви­си­мо­сти от вза­им­ной ори­ен­та­ции век­то­ра рав­но­дей­ству­ю­щей силы и пе­ре­ме­ще­ния тела ра­бо­та может быть по­ло­жи­тель­ной, от­ри­ца­тель­ной и рав­ной нулю.

Конспект

Механическая работа (А)
Физическая величина, характеризующая результат действия силы и численно равная скалярному произведению вектора силы и вектора перемещения, совершенного под действием этой силы.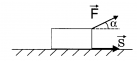
A=Fscosα	A=Fscosα
Работа не совершается, если: 1.Сила действует, а тело не перемещается. Например: мы действуем с силой на шкаф, но не можем сдвинуть.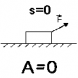
2.Тело перемещается, а сила равна нулю или все силы скомпенсированы. Например: при движении по инерции работа не совершается.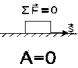
3. Угол между векторами силы и перемещения (мгновенной скорости) равен 900(cosα=0). Например: центростремительная сила работу не совершает.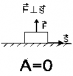
Если вектора силы и перемещения сонаправлены (α=00, cos0=1), то A=Fs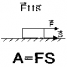
Если вектора силы и перемещения направлены противоположно (α=1800, cos1800 = -1), то A= -Fs(например, работа силы сопротивления, трения).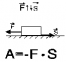
Если угол между векторами силы и перемещения 00 < α < 1800, то работа положительна.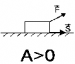
Если угол между векторами силы и перемещения 00 < α < 1800, то работа положительна.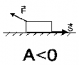
Если на тело действует несколько сил, то полная работа (работа всех сил) равна работе результирующей силы.
Единицы работы.
В международной системе единиц (СИ): [А] = Дж = Н • м Механическая работа равна одному джоулю, если под действием силы в 1 Н оно перемещается на 1 м в направлении действия этой силы.	1Дж = 1Н • 1м
Мощность
Мощность - физическая величина, характеризующая скорость совершения работы и численно равная отношению работы к интервалу времени, за который эта работа совершена. Мощность показывает, какая работа совершается за единицу времени.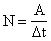
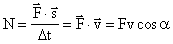
Единицы мощности В международной системе единиц (СИ): 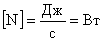Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.	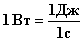1 л.с. (лошадиная сила) ≈ 735 Вт