Различные виды уравнения прямой на плоскости. Угол между прямыми.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 не равно 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Для решение задач уравнений используют специальный вид уравнения прямой.
Векторное параметрическое уравнение прямой
Векторное параметрическое уравнение прямой задается вектором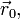 
конец которого лежит на прямой, и направляющим вектором прямой 
Параметр 
пробегает все действительные значения.
]Параметрические уравнения прямой
Параметрические уравнения прямой могут быть записаны в виде:
где — производный параметр, 
— координаты 
и 
направляющего вектора прямой. При этом
Каноническое уравнение прямой
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где 
— координаты и направляющего вектора прямой, 
и 
координаты точки, принадлежащей прямой.
Угол межу прямыми:
Пусть прямые 
и 
заданы каноническими уравнениями 
и 
Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых: 
Тогда
|
Если 
то 
Если 
, то 
или 
.
Прямая и плоскость в пространстве.
1. Условия параллельности и перпендикулярности.
Пусть заданы прямая:
И плоскость: Ах + Ву + С = 0
Прямая параллельная плоскости в том и только в том случае, когда ее направляющий вектор a={l; m; n} перпендикулярен нормальному вектору N= { A; B; C} плоскости. Отсюда получаем условие параллельности прямой и плоскости: Al+Bm+Cn=0
Прямая перпендикулярна плоскости в том и только в случае, когда ее направляющий вектор коллинеарен нормальному вектору плоскости. Отсюда получаем условие перпендикулярности прямой и плоскости: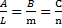 
2.Угол между прямой и плоскостью:
Основная задача линейного программирования. Геометрический метод решения задачи ЛП с двумя переменными.
Основная задача линейного программирования состоит в следующем. Задана система
(6.10)
m линейных алгебраических уравнений с n неизвестными x1,...,xn и линейная форма относительно этих же неизвестных:
F = c1x1 +... + cnxn. (6.11)
Требуется среди всех неотрицательных решений системы (10) выбрать такое, при котором форма F принимает наименьшее значение (минимизируется).
Определение: Система (6.10) называется системой ограничений данной задачи.
Сами равенства (6.10) называются ограничениями-равенствами. Отметим, что кроме ограничений-равенств в основу задач входят также ограничения-неравенства x1≥0,...,xn≥0
Определение: Всякое неотрицательное решение x1(0),...,xn(0)(xi(0)≥0; i=1,...,n) системы (6.10) назовем допустимым. Допустимое решение часто называют планом задачи линейного программирования.
Определение: Допустимое решение системы (6.10), минимизирующее форму F, назовем оптимальным.
Геометрический метод решения задачи ЛП с двумя переменными.
(8)
является полуплоскость. Для того, чтобы определить, какая из двух полуплоскостей соответствует этому неравенству, нужно привести его к виду 
или 
. Тогда искомая полуплоскость в первом случае расположена выше прямой a 0 + a 1 x 1 + a 2 x 2 = 0, а во втором - ниже нее. Если a 2=0, то неравенство (8) имеет вид 
; в этом случае получим либо 
- правую полуплоскость, либо 
- левую полуплоскость.
Областью решений системы неравенств является пересечение конечного числа полуплоскостей, описываемых каждым отдельным неравенством. Это пересечение представляет собой многоугольную область G. Она может быть как ограниченной, так и неограниченной и даже пустой (если система неравенств противоречива).
Область решений G обладает важным свойством выпуклости. Область называется выпуклой, если произвольные две ее точки можно соединить отрезком, целиком принадлежащим данной области. На рис. показаны выпуклая область G 1и невыпуклая область G 2. В области G 1 две ее произвольные точки А 1 и В 1 можно соединить отрезком, все точки которого принадлежат области G 1. В области G 2 можно выбрать такие две ее точки А 2 и В 2, что не все точки отрезка А 2 В 2принадлежат области G 2.
Опорной прямой называется прямая, которая имеет с областью по крайней мере одну общую точку, при этом вся область расположена по одну сторону от этой прямой. На рис. показаны две опорные прямые l 1 и l 2, т. е. в данном случае прямые проходят соответственно через вершину многоугольника и через одну из его сторон.
Основные понятия теории вероятностей. Операции над событиями.
Для изучения законов теории вероятностей введем основные понятия. Одним из них является понятие события.
Определение: Событие -явление, которое происходит в результате осуществления какого-либо комплекса условий.
Осуществление комплекса- испытание или опыт.
Сами испытания проводятся человеком или природой. Условия могут меняться помимо воли испытателя, поэтому исходом испытания может быть не ожидаемое событие, а какое-либо другое заранее неизвестное, которое называется случайным.
Определение: Случайное событие- это событие, которое может произойти или не произойти в результате одного испытания.
Обозначение событий- заглавные буквы латинского алфавита: A, B, C, D и т.д..
Примеры: Испытание- бросание монеты. Случайные события- выпадение герба или цифры.
Испытание- выстрел по мишени. Случайные события- выбивание количества очков от 0 до 10.
Рассмотрим пример: из урны, содержащей 5 красных шаров, вынимают два шара. Событие - оба шара- красные произойдет обязательно, а событие- один из них белый- произойти не может. Первое из этих событий называется достоверным, а второе -невозможным.
Определения:
Достоверное событие- это событие, которое обязательно произойдет в результате испытания.
Невозможное событие- это событие,, которое не может произойти в результате испытания.
В результате испытания может появиться то или иное событие. Причем возможны различные ситуации. Рассмотрим примеры. При бросании монеты возможны события- выпадение герба и выпадение цифры. Но одновременно эти события произойти не могут. При бросании игральной кости(кубика) может выпасть любая из шести ее граней, т.е. произойти любое из событий- выпадение от 1 до 6 точек (очков). Но никакие две и более граней одновременно появиться не могут. Такие события называют несовместными.
Определение: События А и В называются несовместными, если наступление одного из них исключает появление другого.
Теперь рассмотрим другую ситуацию. Проводим испытание- бросание кубика. Рассмотрим события: А- появление четного количества очков, В- появление количества очков, кратных трем. Эти два события могут произойти одновременно при выпадении 6 очков. Такие события называются совместными.
Определение: События А и В называются совместными, если в результате данного испытания появление одного не исключает появление другого.
По отношению к двум событиям, ожидаемым при проведении одного испытания, может возникнуть такая ситуация, когда не появление одного из них обязательно повлечет за собой появление другого. Такие события называются противоположными. Обозначение: для события А противоположным является А (не А).
Определение: События А и А называются противоположными или взаимно дополнительными, если не появление одного влечет появление другого.
Пример: испытание- контрольная работа. События- студент справился с работой и- не справился. В результате испытания обязательно произойдет либо первое, либо второе.
Рассмотрим список событий, которые могут произойти в результате одного испытания. Испытание- выстрел по мишени. События:
Аi- выбито i очков, где i=0-10;
В- выбито менее 10 очков;
С- выбито четное количество очков.
События Аi, где i=0-9, влекут за собой событие В; События А0, А2, А4, А6, влекут за собой событие С.
Говорят, что события Аi, где i=0-9, благоприятствуют событию В; А0, А2, А4, А6- благоприятствуют событию С.
Определение: Событие А называется благоприятствующим событию В, если появление события А влечет за собой появление события В.
Рассмотрим примеры перечисления всех возможных благоприятствующих событий для какого- либо данного события.
Испытание- бросание двух одинаковых кубиков. Событие- выпадение очков, сумма которых равна 6.
Для данного события возможны три благоприятствующих А1, А2 и А3.
С понятием благоприятствующее событие связано понятие - полная группа событий. Введем его на конкретном примере.
Рассмотрим группы событий испытания - выстрел по мишени:
1. Аi, i=0-10, выбивание i очков;
2. Четное В и нечетное С количество очков;
3. Выбивание очков меньше 5- событие D, выбивание очков больше 4 - событие Е.
В каждой группе какое -либо событие в результате испытания обязательно произойдет, причем появление одного из них исключает появление всех остальных. Такие события называются полной группой событий.
Определение: Если группа событий такова, что в результате испытания обязательно должно произойти хотя бы одно из них и любые два из них несовместны, то эта группа событий называется полной группой.
Каждое событие из полной группы называется элементарным событием. Каждое элементарное событие - равновозможное, т.к. нет оснований считать, что какое-либо из них более возможное, чем любое другое событие полной группы.
Два противоположных события составляют полную группу.
Составим полную группу событий для испытания- подбрасывание трех монет одновременно (без учета порядка следования).
Выпадение герба обозначим Г, цифры- Ц. Каждое элементарное событие запишем в виде сочетания этих обозначений: ГГГ, ГЦЦ, ГГЦ, ЦЦЦ. Полная группа состоит из 4-х элементарных событий. В результате испытания обязательно выпадет какая-либо из этих комбинаций.
Операции над событиями.
Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.
Определение. Объединением или суммой событий Аk называется событие A, которое означает появление хотя бы одного из событий Аk.
Определение. Пересечением или произведением событий Ak называется событие А, которое заключается в осуществлении всех событий Ak.
Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.
Определение. Дополнительным к событию А называется событие, означающее, что событие А не происходит.
Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.
Совокупность всех элементарных исходов опыта называется пространством элементарных событий.
16. Аксиоматическое построение теории вероятностей. Классическая вероятностная схема.
При аксиоматическом построении теории вероятностей первичным понятием является не элементарное случайное событие, а просто элементарное событие любой природы. Множество таких событий образует поле элементарных событий 
Из подмножества данного множества составляются некоторые ансамбли, которые и носят название случайного события. Множество таких событий образует поле событий 
. На этом поле случайных событий вводится числовая функция, называемая вероятностью и определяемая следующими аксиомами.
Аксиома 1. Каждому случайному событию 
из поля событий 
поставлено в соответствие неотрицательное число 
называемое вероятностью, такое, что
Аксиома 2. Вероятность достоверного события 
равна единице:
Аксиома 3. Вероятность суммы (объединения) двух несовместных событий равна сумме вероятностей этих событий:
Примечания:
· Рассмотрим теперь следствие, которое служит примером использования этих аксиом. Пусть 
– пустое множество событий, иначе говоря, 
означает отсутствие событий. Тогда
(
) = 
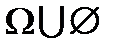,и 
не имеет общих элементов с 
. Следовательно:
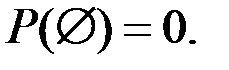(1.14)
· Аксиоматический подход позволяет с более общих позиций подойти к построению теории вероятностей и преодолевает некоторые недостатки классического и статистического определений вероятности событий. Однако для большинства практических задач рассмотренные ранее определения вероятностей событий оказываются достаточно удобными и надежными, так что в дальнейшем будем опираться именно на них. В этом случае третья аксиома должна быть выражена на основе доказательной базы, что и будет сделано позднее.