ЭЛЕМЕНТЫЛИНЕЙНОЙ АЛГЕБРЫ
1. Матрицы. Действия над матрицами.
2. Вычисление определителей.
3. Методы решения систем линейных алгебраических уравнений: метод Крамера, метод Гаусса, матричный метод.
Решение типового примера
Пример 1.1. Решить систему уравнений:
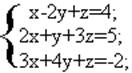
Решение.
а)По формуле Крамера:
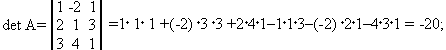
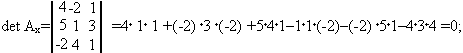
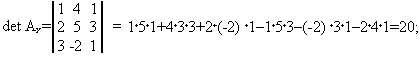


б)Метод Гаусса:
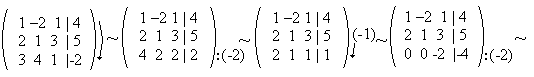
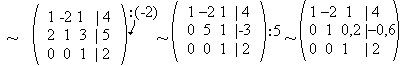
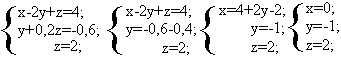
Ответ: x=0; y=-1; z=2;
в)Матричный способ:
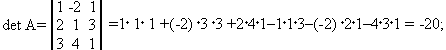
А11=1(1  1–3
1–3  4)=-11 А12=-1(2
4)=-11 А12=-1(2  1–3
1–3  3)=7 А13=1(2
3)=7 А13=1(2  4–3
4–3  1)=5
1)=5
А21=-1(-2  1–1
1–1  4)=6 А22=1(1
4)=6 А22=1(1  1–1
1–1  3)=-2 А23=-1(1
3)=-2 А23=-1(1  4+2
4+2  3)=-10
3)=-10
А31=1(-2  3–1
3–1  1)=-7 А32=-1(1
1)=-7 А32=-1(1  3–1
3–1  2)=-1 А33=1(1
2)=-1 А33=1(1  1+2
1+2  2)=5
2)=5
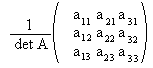
А-1=

А-1=
Ответ: x=0; y=-1; z=2;
Задачи контрольной работы
В задачах 1.1- 1.20 решить заданную систему линейных уравнений:
· пользуясь формулами Крамера;
· методом Гаусса;
· матричным методом;
1. 1 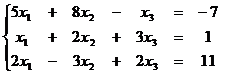 1.2
1.2 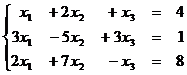
1.3 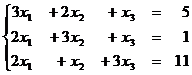 1.4
1.4 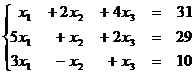
1.5 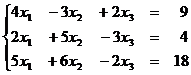 1. 6
1. 6 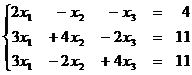
1.7 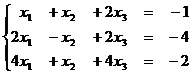 1.8
1.8 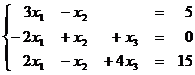
1. 9 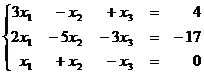 1.10
1.10 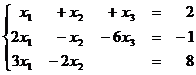
1.11 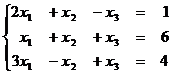 1.12
1.12 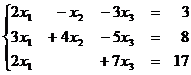
1.13 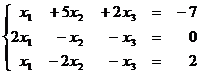 1.14
1.14 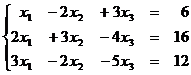
1.15 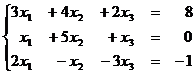 1.16
1.16 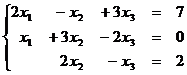
1.17 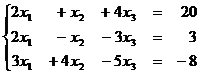 1.18
1.18 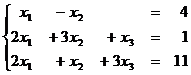
1.19 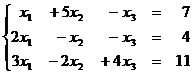 1.20
1.20 
ЭЛЕМЕНТЫВЕКТОРНОЙ АЛГЕБРЫНА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Элементы векторной алгебры на плоскости
Программные вопросы
1. Сумма и разность двух векторов.
2. Коллинеарность и компланарность векторов.
3. Проекция вектора на ось.
4. Разложение вектора в системе орт на плоскости и в пространстве. Координаты вектора.
5. Свойства скалярного произведения векторов.
6. Угол между векторами.Длина вектора по его координатам.
7. Условие перпендикулярности двух векторов.
8. Вектор, перпендикулярный двум данным векторам.
9. Площадь треугольника, построенного на двух векторах.
10. Объём пирамиды с вершинами в заданных точках.
Решение типового примера
Пример 2.1.
Даны координаты точек 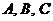 . Пусть
. Пусть  .
.
Требуется:
1) записать векторы 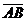 и
и 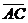 в системе орт
в системе орт 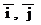 и найти длины этих векторов;
и найти длины этих векторов;
|
|
2) найти орт вектора 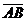 ;
;
3) изобразить векторы 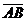 и
и 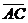 в координатной плоскости
в координатной плоскости 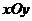 ;
;
4) найти вектора 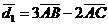 и
и 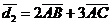 аналитически и геометрически.
аналитически и геометрически.
Решение.
1) Известно, что произвольный вектор 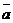 представляется в системе орт
представляется в системе орт 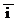 ,
, 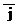 по формуле:
по формуле:
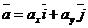 , (1)
, (1)
где 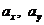 – координаты вектора
– координаты вектора 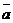 в системе координат
в системе координат 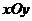 .
.
Если заданы точки 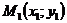 ,
,  , то для вектора
, то для вектора 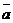 =
= 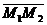
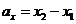 ,
, 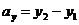 (2)
(2)
Воспользовавшись (2) и координатами точек 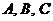 , получим:
, получим:
 или
или  . Тогда
. Тогда 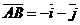 .
.
 или
или  . Тогда
. Тогда 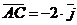 .
.
Если вектор 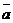 задан своими координатами, то его длина (модуль) вычисляется по формуле:
задан своими координатами, то его длина (модуль) вычисляется по формуле:
 (3)
(3)
Используя формулу (3), получаем длины векторов 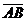 и
и 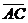 :
:
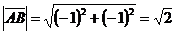 ,
,
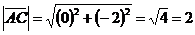 .
.
2) Известно, что орт вектора 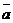 можно найти по формуле:
можно найти по формуле:

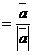 , т.е.
, т.е. 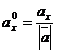 ,
,  (4)
(4)
Воспользовавшись формулами (4), получим: 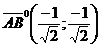 .
.

| ||||||||||||

|
|

| |||||||||||||||||||||||||||||
|
|
3) Найдем векторы 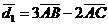 и
и 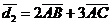 аналитически.
аналитически.
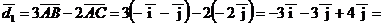
 .
.
Таким образом, 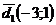 .
.
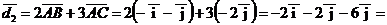
 .
.
Таким образом, 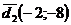 (рис.1).
(рис.1).
Найдем векторы 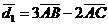 и
и 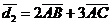 геометрически (рис.2).
геометрически (рис.2).
Задачи контрольной работы
Даны координаты точек 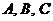 . Требуется:
. Требуется:
1) записать векторы 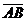 и
и 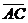 в системе орт
в системе орт 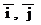 и найти длины этих векторов;
и найти длины этих векторов;
2) найти орт вектора 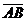 ;
;
3) изобразить векторы 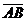 и
и 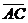 в координатной плоскости
в координатной плоскости 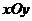 ;
;
4) найти вектора 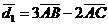 и
и 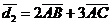 аналитически и геометрически.
аналитически и геометрически.
| 2.1 А(-8; -3), В(4; -12), С(8; 10) | 2.11 А(4; 0), В(7; 4), С(8; 2) |
| 2.2 А(-5; 7), В(7; -2), С(11; 20) | 2.12 А(-2; 7), В(10; -2), С(8; 12) |
| 2.3 A(3; -1), В(7; 1), С(4; -2) | 2.13 А(-6; 8), В(6; -1), С(4; 13) |
| 2.4 А(-12; -1), В(0; -10), С(4; 12) | 2.14 А (0; 2), В(3; 6), С(4; 4) |
| 2.5 А(-10; 3), В(2; 0), С(6; 22) | 2.15 А(-10; 5), В(2; -4), С(0; 10) |
| 2.6 А(0; 0), В(3; 4), С(4; 2) | 2.16 А(-4; 12), В(8; 3), С(6; 17) |
| 2.7 А(-9; 6), В(3; -3), С(7; 19) | 2.17 А(-3; 10), В(9; 1), С(7; 15) |
| 2.8 А(3; -3), В(6; 1), С(7; -1) | 2.18 А(4; -3), В(7; 1), С(8; -1) |
| 2.9 А(1; 0), В(13; -9), С(17; 13) | 2.19 А(2; -2), В(5; 2), С(6; 0) |
| 2.10 А(0; 2), В(12; -7), С(16;15) | 2.20 А(-1; 1), В(2; 5), С(3; 3) |
Элементы векторной алгебры в пространстве
Решение типового примера
Пример 2.2.
Даны координаты вершин пирамиды ABCD. Пусть А(0; 0; 1), В(2; 3; 5), С(6; 2; 3), D(3; 7; 2).
Требуется:
1) Записать векторы 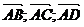 в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) Найти угол между векторами 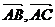 ;
;
3) Найти проекцию вектора  на вектор
на вектор 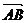 ;
;
4) Найти площадь грани АВС;
5) Найти объём пирамиды ABCD;
Решение.
1. Известно, что произвольный вектор 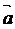 представляется в системе орт
представляется в системе орт  по формуле
по формуле

 (1)
(1)
где 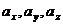 координаты вектора
координаты вектора 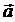 в системе координат, порождённой ортами, причём
в системе координат, порождённой ортами, причём
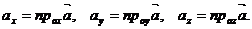
Если заданы точки 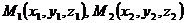 , то для вектора
, то для вектора 

то есть
 (2)
(2)
Воспользовавшись формулой (2) и координатами заданных точек A, B, C, D, получим:
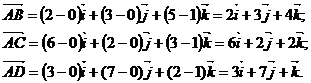
Если вектор 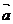 задан формулой (1),то его модуль вычисляется следующим образом:
задан формулой (1),то его модуль вычисляется следующим образом:
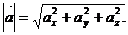 (3)
(3)
Используя формулу (3), получаем модули найденных векторов:
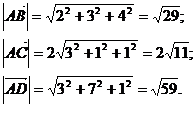
Известна формула
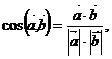
где 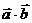 скалярное произведение векторов
скалярное произведение векторов 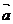 и
и 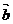 , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:
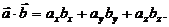
У нас

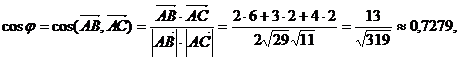
то есть 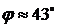 .
.
3. Известно, что
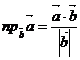 ,
,
то есть в нашем случае
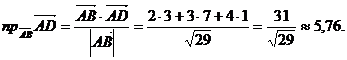
4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах 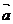 и
и 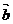
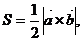
где 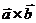 векторное произведение векторов, которое можно вычислить по следующему правилу:
векторное произведение векторов, которое можно вычислить по следующему правилу:
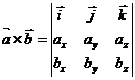 .
.
В нашем примере 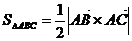 , причём
, причём

Таким образом,
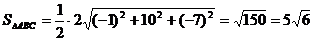 (кв. ед.).
(кв. ед.).
Объём пирамиды, построенной на трёх некомпланарных векторах  можно найти по формуле
можно найти по формуле

где 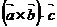 смешанное произведение векторов, которое вычисляется следующим образом:
смешанное произведение векторов, которое вычисляется следующим образом:
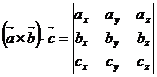 .
.
У нас 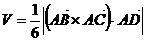 , где
, где
 ,
,
то есть 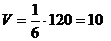 (куб.ед.).
(куб.ед.).
Задачи контрольной работы
Даны координаты вершин пирамиды ABCD.
Требуется:
1) Записать векторы 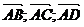 в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) Найти угол между векторами 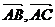 ;
;
3) Найти проекцию вектора  на вектор
на вектор 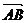 ;
;
4) Найти площадь грани АВС;
5) Найти объём пирамиды ABCD.
| 2.1 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.11 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.2 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.12 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.3 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.13 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.4 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.14 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.5 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.15 (2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.6 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.16 A(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.7 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.17 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.8 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.18 A(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.9 А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.19 A(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |
| 2.10 A(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). | 2.20 A(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). |