Алгоритм группировки с равными интервалами

ЛАБОРАТОРНАЯ РАБОТА № 1

 

ГРУППИРОВКА И ПОСТРОЕНИЕ ГИСТОГРАММЫ.

ОПРЕДЕЛЕНИЕ ВЫБОРОЧНЫХ ХАРАКТЕРИСТИК

Введение

Исходные данные: выборка ,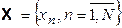

Здесь - значение регистрируемого признака для 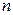-го элемента выборки,

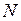- объем выборки.

 

Признак - свойство (характеристика) элемента выборки (единицы статистической совокупности).

 

Например:

 

Единица статистической совокупности	Признак
Фирма	Прибыль, количество сотрудников и т.п.
Магазин	Площадь, товарооборот и т.п.
Сотрудник	Возраст, заработная плата и т.п.
Студент	Оценка на экзамене, средний балл и т.п.
Автомобиль	Расход топлива, максимальная скорость и т.п.

 

В качестве выборки используйте данные из файла Data.txt

Выберите анализируемый признак согласно номеру Вашего варианта:

 

Признак	Номер варианта
Время разгона
Вес
Мощность
Объём

Задание 1. ГРУППИРОВКА И ПОСТРОЕНИЕ ГИСТОГРАММЫ

Группировка - это распределение единиц совокупности по группам в соответствии с группировочным признаком.

Благодаря группировке данные приобретают систематизированный вид. На основе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения и изучения взаимосвязей.

 

Алгоритм группировки с равными интервалами

1. По формуле Стерджесса

с учётом округления определяем рекомендуемое количество групп, которое может быть подкорректировано.

 

2. Находим величину интервала

,

где 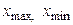– наибольшее и наименьшее значение признака в исследуемой совокупности.

 

3. Определяем границы (крайние точки) каждого интервала

, .

Нижняя граница первого интервала .

Таким образом,

1-й интервал имеет границы от до : ,

2-й интервал имеет границы от до : ,

…

-й интервал имеет границы от до : .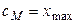

 

4. Находим центральные значения (середину) интервалов

,

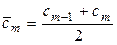5. Находим численность каждой из групп (частоты) , .

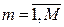Для этого подсчитаем число элементов выборки, попавших в каждый из интервалов.

6. Находим относительную частоту (частость) ─ долю элементов -й группы в выборке , .

Очевидно, что .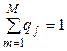

В результате группировки единицы выборки распределяются по группам на основе значений изучаемого признака.

Представим результаты группировки в табличной форме.

№ группы	Интервал	Середина интервала	Среднее по группе	Частота	Относительная частота
…	…	…	…	…

 

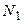
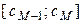
В результате группировки обычно определяют, какие именно объекты попали в 1-ю, 2-ю и другие группы.

Графическое представление распределения исследуемого признака осуществляется с помощью гистограммы (столбиковой диаграммы).

 

Постройте гистограмму частот для исследуемого признака

Постройте гистограмму относительных частот для исследуемого признака

 

С помощью гистограммы может быть представлена непараметрическая оценка плотности вероятности. Для этого высоты прямоугольников (сплошных столбиков) строятся равными , а основание ─ величине интервалов . В данном случае интервалы равны между собой .

Задание 2. ОПРЕДЕЛЕНИЕ ВЫБОРОЧНЫХ ХАРАКТЕРИСТИК

Рассчитайте выборочные характеристики, используя данные согласно номеру Вашего варианта.

Выборочные характеристики	Для не сгруппированных данных	Для сгруппированных данных
Среднее значение
Медиана	− для нечетного , − для четного	─
Выборочные показатели вариации (степени рассеяния) признака
Размах вариации		─
Квартильный размах		─
Среднее линейное отклонение
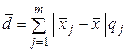
Среднее квадратическое отклонение
Дисперсия
Коэффициент вариации

В таблице обозначено:

─ -й элемент вариационного ряда (упорядоченных выборочных значений),

─ третий квартиль,

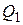─ первый квартиль.

Примечание: При расчете по сгруппированным данным в качестве используются средние по группам значения. Если эти значения неизвестны, то используют центральные значения интервалов, что приводит к приближенным результатам.

 

Если значение коэффициента вариации коэффициента вариации не превышает 33%, то исследуемая совокупность считается количественно однородной. Если значение коэффициента вариации коэффициента вариации меньше 25%, то вариация считается слабой.