Переменный ток в отличие от постоянного не распределяется равномерно по сечению проводника, а имеет большую плотность у его поверхности. Это явление называют скин-эффектом (по-английски skin - кожа).
Рассмотрим, для простоты, бесконечный однородный цилиндрический провод (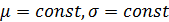 ) по которому течет переменный ток. Будем предполагать, что полный ток I= I0 eiwt, протекающий через сечение провода, известен.
) по которому течет переменный ток. Будем предполагать, что полный ток I= I0 eiwt, протекающий через сечение провода, известен.
Пренебрегая токами смешения по сравнению с током проводимости и считая процесс установившимся, т. е. зависящим от времени по закону eiwt, получим, после сокращения на множитель eiwt, уравнения Максвелла в виде:
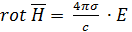 (1)
(1)
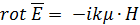 (2)
(2)
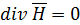 (3)
(3)
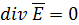 (4)
(4)
где 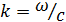 . Уравнения (3) и (4) в данном случае, очевидно, следуют из уравнений (1) и (2).
. Уравнения (3) и (4) в данном случае, очевидно, следуют из уравнений (1) и (2).
Введем цилиндрическую систему координат (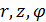 ) так, чтобы ось z совпадала с осью провода. Тогда в силу осевой симметрии тока все величины можно считать зависящими только от переменной r.
) так, чтобы ось z совпадала с осью провода. Тогда в силу осевой симметрии тока все величины можно считать зависящими только от переменной r.
Так как в нашем случае вектор Е направлен вдоль оси z, то из уравнений (1) и (2) будем иметь:
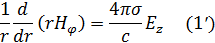
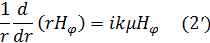
Исключая отсюда H 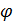 , найдем:
, найдем:
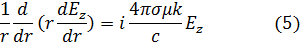
Введем граничное условие на поверхности провода при r=R. Для этого воспользуемся тем, что нам известен полный ток I0, протекающий по цилиндру.
Запишем первое уравнение Максвелла (1) в интегральной форме:
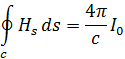
где С — контур, охватывающий провод, Нs — тангенциальная составляющая вектора H на С. Если в качестве такого контура взять окружность r=R, то получим:
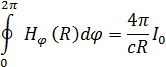
или
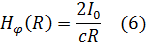
Отсюда, пользуясь соотношением (2), находим:
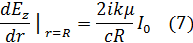
Таким образом, мы должны решить уравнение Бесселя:
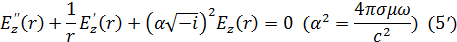
при граничном условии -
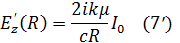
и условии ограниченности при r = 0: 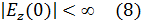
Общее решение уравнения (5') имеет вид:
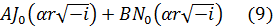
где J0 и N0— функции Бесселя первого и второго рода, А и В — постоянные, подлежащие определению.
Функция N0 имеет логарифмическую особенность при r=0. Поэтому в силу условия (8) B= 0 и, следовательно,
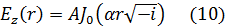
Коэффициент A определим из граничного условия (7):
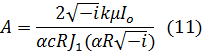
Отсюда для плотности тока получаем:
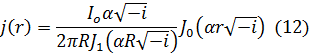
В правой части этой формулы стоят функции Бесселя от комплексного аргумента:
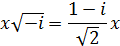
Обычно пользуются для этих функций следующими обозначениями:
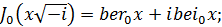
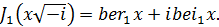
Нетрудно найти выражения для вещественных функций ber x и bei x, пользуясь разложением функций Бесселя в ряд. Например,
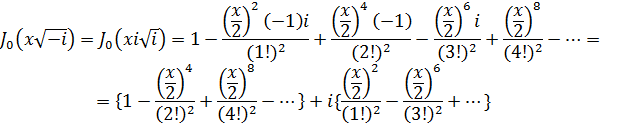
откуда получаем:
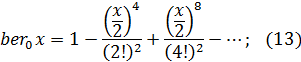
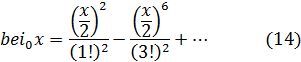
Нетрудно убедиться подобным же образом, что
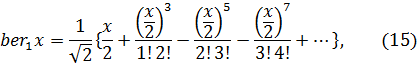
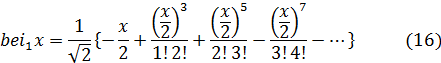
В приложениях встречаются также производные: ber0 ' x и bei 0' x причем
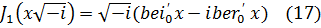
Пользуясь введенными функциями, выражение (12) для тока можно записать в виде:
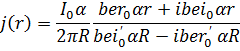
или
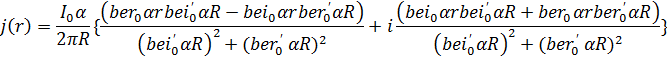
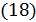
Вычисляя абсолютную величину этого выражения, получим:
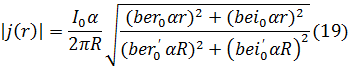
Величиной, характеризующей распределение тока по сечению, является отношение:
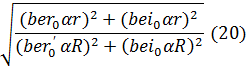
Так же отмечу, что скин-эффект широко используется на практике для закалки металлов.
Заключение
В данной курсовой работе рассмотрено уравнение Ф.В. Бесселем, относительно его применения в таких науки как математика, физика, астрономия и др.
Доказали такие важные свойства уравнения Бесселя как
Применили данное уравнение к такому физическому процессу как скин-эффект.
Список литературы:
1. Агошков В.И., Дубовский П.Б., Шутяев В.П. Методы решения задач математической физики / Под ред. Г.И. Марчука: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2002. – 320 с.
2. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. – 4-е изд., испр. – М.: ФИЗМАТЛИТ, 2003. – 688 с.
3. Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учебник. 7-е изд. / Тихонов А.Н., Самарский А.А. – М.: Изд-во МГУ; Изд-во «Наука», 2004. – 798 с.
4. Шарма Дж. Н., Сингх К. Уравнения в частных производных для инженеров. М.: – Техносфера, 2002. – 320 с.
5. Араманович И.Г., Левин В.И. Уравнения математической физики. – М.: Изд-во «Наука», 1964. – 286 с.
6. Бицадзе А.В. Уравнения математической физики: Учебник. – 2-е изд., перераб. и дополненное. – М.: Наука, Главная редакция физико-математической литературы, 1982. – 336 с.
7. Владимиров В.С. Уравнения математической физики. – М.: Изд-во «Наука», 1967. – 436 с.
8. Власова Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 700 с.
9. Вазов В., Форсайт Дж. Разностные методы решения дифференциальных уравнений в частных производных. – М.: Изд-во «Мир», 1963. – 488 с.
10. Годунов С.Г. Уравнения математической физики. – М.: Изд-во «Наука», 1971. – 416 с.
11. Джеффрис Г., Свирлс Б. Методы математической физики. – М.: Изд-во «Мир» Выпуск 1, 1969. – 424 с.
12. Джеффрис Г., Свирлс Б. Методы математической физики. – М.: Изд-во «Мир» Выпуск 2, 1970. – 352 с.
13. Джеффрис Г., Свирлс Б. Методы математической физики. – М.: Изд-во «Мир» Выпуск 3, 1970. – 344 с.
14. Зайцев В.Ф., Полянин А.Д. Справочник по дифференциальным уравнениям с частными производными первого порядка. – М.: ФИЗМАТЛИТ, 2003. – 416 с.
15. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Дифференциальные уравнения математической физики. – М.: Выс.школа, 1962. – 767 с.
16. Кузнецов А.В. Методы математической физики: Учеб. пособие / Яросл. гос. ун-т. Ярославль, 2004. – 200 с.
17. Курант Р., Гильберт Д. Методы математической физики. – М.: ОГИЗ Том 1, 1933. – 525 с.
18. Полянин А.Д. Справочник по линейным уравнениям математической физики. – М.: ФИЗМАТЛИТ, 2001. – 576 с.
19. Прямые и обратные задачи математической физики: Сборник / Под ред. А.Н. Тихонова, А.А. Самарского. – М.: Изд-во Моск. Ун-та, 1991. – 258 с.
20. Сабитов К.Б. Уравнения математической физики: Учеб. пособие для вузов. – М.: Высш. шк., 2003. – 255 с.
21. Уроев В.М. Уравнения математической физики. – М., В. Секачев, ИФ «Яуза», 1998. – 373 с.