Частные случаи уравнения Бесселя.

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

«Московский государственный индустриальный университет»

Филиал ФГБОУ ВПО «МГИУ» в г. Сергиевом Посаде

Кафедра «Прикладная математика и информатика»

Курсовая работа

по дисциплине:

 

«Методы математической физики (линейные и нелинейные уравнения физики)»

 

на тему: «________________________________________________________»

 

Выполнил:

 

Студен Семенкин С.А.

 

Группа 6741 курс III семестр VI

 

Проверил:

 

Преподаватель Андреева Н.Ю.

 

 

Дата сдано: «_______»____________200___г.

 

Дата проверено: «_______»____________200___г.

 

Оценка работы ____________________

 

 

Сергиев Посад

Содержание

Введение……………………………………………………………..….….3

1. Уравнение Бесселя………………………………………………......5

2. Частные случаи уравнения Бесселя……………………….………9

3. Ортогональность функций Бесселя и их корни…………………..11

4. Применение теории функций Бесселя к анализу скин-эффекту……………………………………………………….……14

Заключение…………………………………………………………....…18

Список литературы……………………………………………….……..19

Вступление

В этой курсовой работе мы познакомимся с уравнением Бесселя и его применением в уравнениях математической физики. Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

 

Фридрих Вильгельм Бессель

— немецкий математик и астроном XIX века. Родился 22 июля 1784 в Миндене. Самостоятельно изучал математику и астрономию, в 1804 вычислил орбиту кометы Галлея. В 1806 стал ассистентом крупного астронома И.Шрётера в Лилиентале, вскоре приобрел репутацию видного астронома-наблюдателя и вычислителя-математика. В этом качестве в 1810 был приглашен в Кёнигсбергский университет для организации обсерватории, директором которой оставался до конца жизни. Полагая, что в результаты наблюдений необходимо вносить поправки, учитывающие наличие самых незначительных факторов, Бессель разработал математические методы коррекции результатов наблюдений. Первой работой в этом направлении стала корректировка положений звезд в каталоге, составленном в 18 в. английским астрономом Дж. Брадлеем. В дальнейшем Бессель сам вел наблюдения за звездами; в 1821-1833 он определил положение более 75 тыс. звезд и составил обширные каталоги, которые легли в основу современных знаний о звездном небе.

Бессель одним из первых измерил параллаксы звезд и расстояние до них. В 1838 определил расстояние до двойной звезды 61 Лебедя, оказавшейся одной из самых близких к Солнечной системе. Наблюдая в течение ряда лет яркие звезды Сириус и Процион, Бессель обнаружил в их траектории такие особенности, которые можно было объяснить только наличием спутников. Эти предположения впоследствии подтвердились: в 1862 был обнаружен спутник Сириуса, а в 1896 — спутник Проциона. Известны работы Бесселя в области геодезии (определение длины секундного маятника, изобретение базисного прибора).

Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:

· электромагнитные волны в цилиндрическом волноводе;

· теплопроводность в цилиндрических объектах;

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Уравнение Бесселя

При решении многих задач математической физики приходят к линейному дифференциальному уравнению:

 

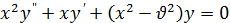(1)

где — постоянная. Это уравнение встречается также во многих вопросах физики, механики, астрономии и т. п. Уравнение (1) называется уравнением Бесселя. Так как уравнение (1) имеет особую точку x = 0, то его частное решение следует искать в виде обобщенного степенного ряда:

 

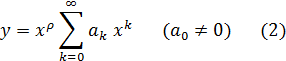
Подставляя ряд (2) в уравнение (1), получим

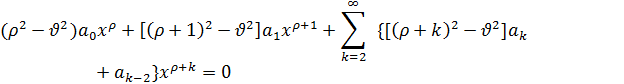
(3)

Приравнивая нулю коэффициенты при различных степенях x, будем иметь:

 

 

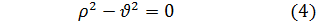
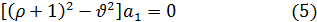
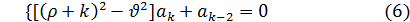
Из первого равенства находим два значения для р: p₁= 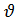и p₂=-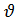

Если мы возьмем первый корень р = , то из формул (5) и (6) получим:

 

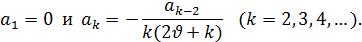
Отсюда следует, что a_2k+1=0 (k=2, 3, 4,…), а коэффициенты с четными индексами определяются, очевидно, по формулам:

 

 

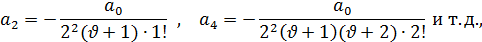
Из которых ясно, что общее выражение для коэффициентов имеет такой вид:

 

 

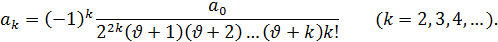
Что касается коэффициента a₀, который был до сих пор со­вершенно произвольным, то выберем его таким образом:

 

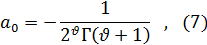
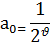
где Г () — гамма-функция, которая определяется для всех поло­жительных значений (а также для всех комплексных значений с положительной вещественной частью) следующим образом:

 

 

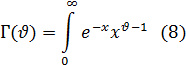
При таком выборе а₀ коэффициент а_2k может быть записан в виде:

 

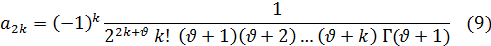
Это выражение может быть упрощено, если воспользоваться одним из основных свойств гамма-функции. Для этого проинтег­рируем правую часть равенства (8) по частям; тогда получим следующую основную формулу:

 

 

 

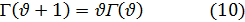
Отметим, что формула (10) дает возможность определить гамма-функцию для отрицательных значений , а также и для всех комплексных значений.

Пусть k — некоторое целое положительное число. Применяя несколько раз формулу (10), получим

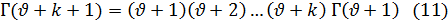
Полагая в этой формуле = 0, найдем, в силу равенства

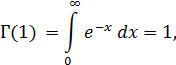
другое важное свойство гамма-функции, выражаемое

 

Г (k+1) = k! (12)

 

С помощью формулы (11) выражение (9) для коэффициента а_2k примет следующий вид:

 

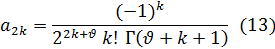
Внося найденные значения коэффициентов а_2k+1 и а_2k в ряд (2), получим частное решение уравнения (1). Это решение носит название функции Бесселя 1-го рода -го порядка и обозначается обычно через J_V (x).

Таким образом,

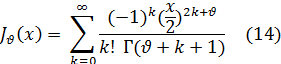
Ряд (14) сходится при любом значении x, в чем нетрудно убе­диться, применяя признак Даламбера.

Используя второй корень p₂ =— 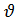, можно построить второе частное решение уравнения (1). Оно может быть получено, оче­видно, из решения (14) простой заменой на — 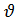, так как урав­нение (1) содержит только ² и не меняется при замене на — :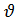

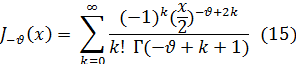
Если не равно целому числу, то частные решения J_V (x) и J-_V (x). уравнения Бесселя (1) будут линейно независимыми, так как разложения, стоящие в правых частях формул (14) и (15), начинаются с разных степеней х. Если же есть целое положи­тельное число n, то в этом случае легко обнаружить линейную зависимость решений J_n(x) и J_-n(x). Действительно, при целом для к = 0, 1, 2,..., n — 1 величина - +k+ 1 принимает целые отрицательные значения или нуль. Для этих значений k: Г(- +k+ 1) = 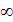, что следует из формулы:

 

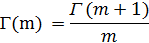
Таким образом, первые n членов в разложении (15) обратятся в нуль и мы получим

 

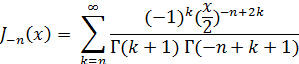
или, положив k= n + l, получим

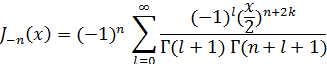
т.е.

 

 

Отсюда следует, что при целом n функции J_n(x) и J_-n(x) линейно зависимы.

Для того чтобы найти общее решение уравнения (1), когда равно целому числу n, необходимо найти второе, линейно-независимое от J_V (x), частное решение. Для этого введем новую функцию Y_v (х), положив

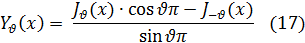
Очевидно, что эта функция также является решением уравне­ния (1), так как она представляет собою линейную комбинацию частных решений J_V (x) и

J-_V (x) этого уравнения. Затем нетрудно убедиться, на основании соотношения (16), что при , равном целому числу n, правая часть равенства (17) принимает неопре­деленный вид . Если раскрыть эту неопределенность по правилу Лопиталя, то в результате ряда выкладок (которые ввиду их сложности здесь не воспроизводятся) получим следующее пред­ставление функции Y_n(x) при целом положительном n:

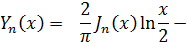
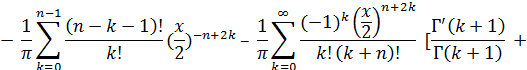
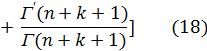
В частном случае, при n = 0, функция Y_o(х) представляется таким образом:

 

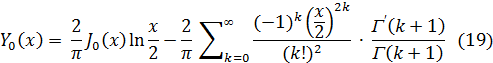
Введенная здесь функция Y_v (х) называется функцией Бесселя 2-го рода -го порядка или функцией Вебера.

Функция Вебера Y_v (х) является решением уравнения Бесселя также и в том случае, когда — целое число.

Функции J_V (x) и Y_v (х), очевидно, линейно независимы, сле­довательно, эти функции при всяком —дробном или целом — образуют фундаментальную систему решений. Отсюда вытекает, что общее решение уравнения (1) может быть представлено в виде

 

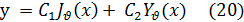
где С₁ и С₂ — произвольные постоянные.

 

Частные случаи уравнения Бесселя.

В математической физике наиболее часто встречаются функ­ции Бесселя

 

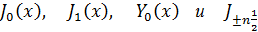где п —целое число.

 

Первые две из этих функций представляются следующими рядами:

 

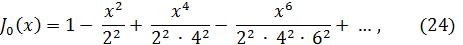
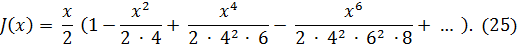
Для них имеются подробные таблицы. Графики функций J₀(x), J₁(x) и У₀(x) приведены на рис.1 и 2.

 

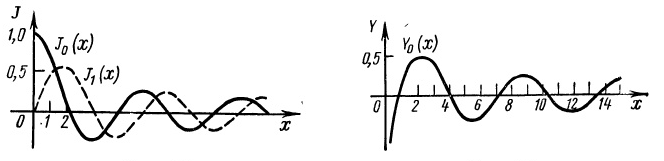
Рис.1 Рис.2

 

Из формулы (23) видно, что вычисление функций J₂(x), J₃(x) и т. д. сводится к вычислению соответствующих значении функций J₀(x) и J₁(x).

Обратимся теперь к функции J_n+1/2 (x), где n — целое число.

Найдем прежде всего значения функций J_1/2 (x) и J_-1/2 (x), для чего обратимся к разложению (14); из него видно, что

 

 

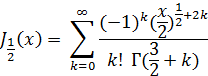
Но из формулы (11) непосредственно вытекает, что

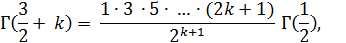
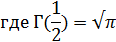
Таким образом,

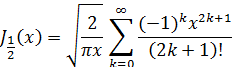
Последняя сумма представляет собой разложение sin x в степен­ной ряд, вследствие чего

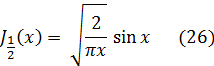
Аналогично, из разложения (15) вытекает, что

 

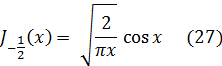
Если теперь воспользоваться формулой (23), то нетрудно видеть, что

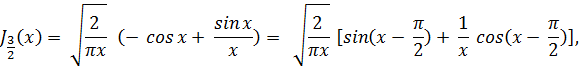
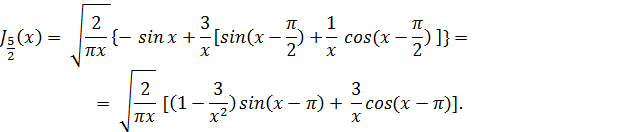
Вообще, функция Бесселя J_n+1/2 (x) при целом n выражается через элементарные функции, а именно:

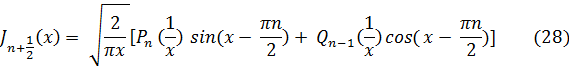
где Р_n (1/x) — многочлен степени n относительно 1/x, а

Q_n-1 (1/x) —многочлен степени n —1, причем P_n(0) = 1, 0_n-1(0)=0. Отсюда следует, что при больших значениях х имеет место асимптотическое представление функции Бесселя:

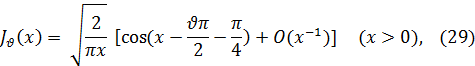
где через О(x^-1) обозначена величина порядка 1/x.

Отметим, что асимптотическая формула (29) справедлива не только при =n+1/2, но и при всех значениях .

 

 

4. Ортогональность функций Бесселя и их корни.

Рассмотрим уравнение

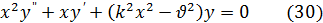
где k — некоторая постоянная, отличная от нуля.

Введем вместо x новую независимую переменную t = kx. Тогда уравнение (30) преобразуется в такое:

 

 

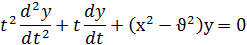
а это есть уравнение Бесселя. Следовательно, функция y=J_v (kx) будет решением уравнения

 

 

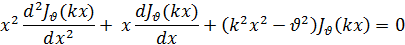
которое разделив на x, можем написать в виде

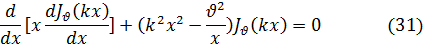
Возьмем два различных значения k и напишем соответствую­щие дифференциальные уравнения:

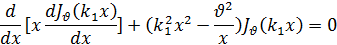
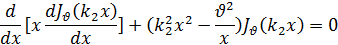
Умножая первое из этих равенств на J_v (k₂ x), а второе— на J_v (k₁ x) и вычитая одно из другого, после несложных преобразований получим:

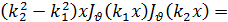
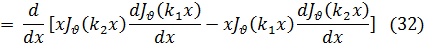
Если теперь воспользоваться формулой (14), то нетрудно убе­диться, что выражение, стоящее здесь в квадратных скобках, может быть разложено по степеням x, причем наинизшая степень х будет х^{2(v+1 )}. Отсюда ясно, что это выражение будет обра­щаться в нуль при х = 0, если > —1. Приняв это во внима­ние, проинтегрируем равенство (32) по некоторому конечному промежутку (0, l); тогда получим

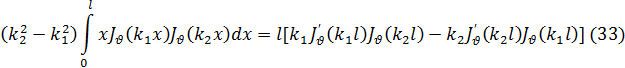
где через (') обозначается, как обычно, дифференцирование по аргументу. При l = 1 эта формула принимает вид:

 

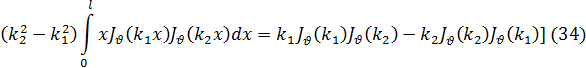
Покажем теперь, что при >—1 функция Бесселя J_V(x) не может иметь комплексных корней. Допустим, что она имеет такой корень а+ib, причем а . В разложении (14) все коэффициен­ты разложения вещественны и, следовательно, функция J₁(x) кроме корня a+ib должна иметь и сопряженный корень a-ib. Обра­тимся к формуле (34) и положим k₁=a+ib и k₂=a+ib; при этом k₁²≠k₂² и формула дает

 

 

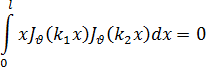
Величины J_V(k₁x) и J_V(k₂x) будут комплексно сопряженными, следовательно, в предыдущей формуле под знаком интеграла стоит положительная величина и эта формула не может иметь места.

Функция Бесселя J_v(x) не может иметь и чисто мнимых корней. Действительно, подставив ± ib в формулу (14), получим разло­жение, содержащее только положительные члены:

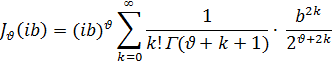
так как, согласно формуле (8), гамма-функция Г(x) принимает положительные значения при х > 0.

Покажем теперь, что функция J_v(x) имеет вещественные корни. Для этого обратимся к асимптотическому разложению функции Бесселя (29):

 

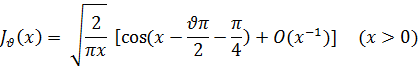
Из этой формулы видно, что при беспредельном удалении x: вдоль положительной части оси Ох второе слагаемое в квадратных скобках стремится к нулю, а первое — бесчисленное множество раз изменяется от -1 к +1. Отсюда непосредственно вытекает, что функция J_v(x) имеет бесчисленное множество вещественных корней.

Таким образом, приходим к следующему результату: если 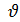> -1, то функция J_v(x)имеет все корни вещественные.

Заметим, кроме того, что из разложения (14), содержащего только четные степени, непосредственно вытекает, что корни J_v(x) будут попарно одинаковыми по абсолютной величине и обратными по знаку, так что достаточно рассматривать только положитель­ные корни.

Пусть k₁= 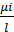, k₂= 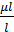, где µ_i и µ_l —два различных положи­тельных корня уравнения.

Тогда формула (33) дает непосредственно следующее свойство ортогональности функций Бесселя:

 

 

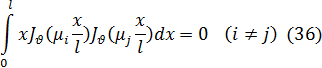
Пусть теперь k= , где µ— положительный корень уравнения (35). Возьмем формулу (33), в которой положим k₁=k₂, k₂ а будем считать переменным и стремящимся к k, тогда получим

 

 

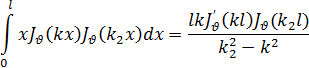
При k₂- > правая часть этого равенства становится неопре­деленной так как числитель и знаменатель стремятся к нулю. Раскрыв эту неопределенность по правилу Лопиталя, получим

 

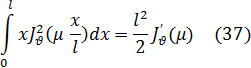
Положив в формуле (22) х=µ и приняв во внимание, что есть корень уравнения (35), получим

 

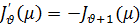
и формулу (37) можно записать еще следующим образом:

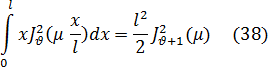
Таким образом, мы имеем

 

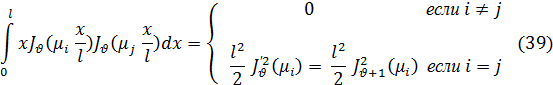
( > -1 )

 

где µ _i и µ _j—положительные корни уравнения J_V(x)=0.

Рассмотрим теперь более общее уравнение

где α и β—заданные вещественные числа.